【算法•日更•第六期】头脑风暴：洛谷P1528 切蛋糕题解

▎（一个没有用处的）前言

　　为什么这次题解特意写明题号呢？因为我发现了这样的事情：

　　

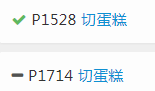
　　所以不要混了，想看P1714题解的同志们可以圆润的滚开了。

　　好了，不说没用的了，切入正题：

---

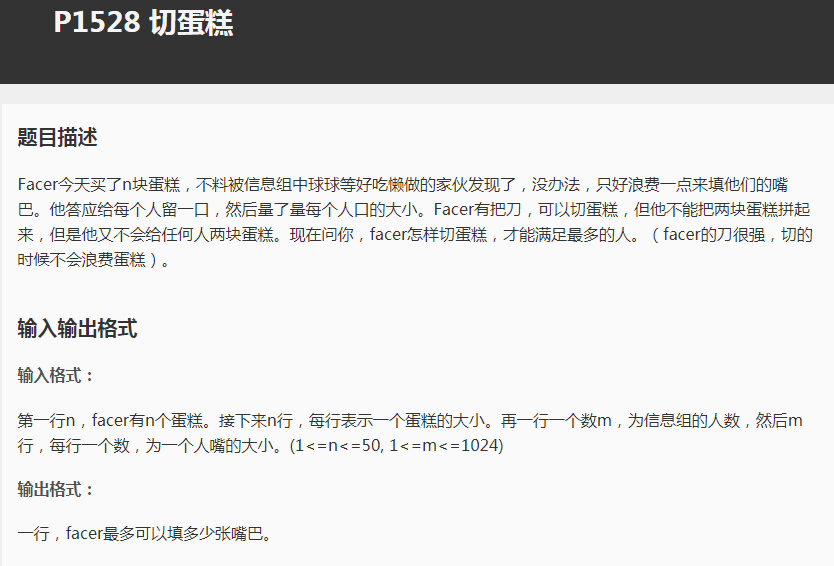
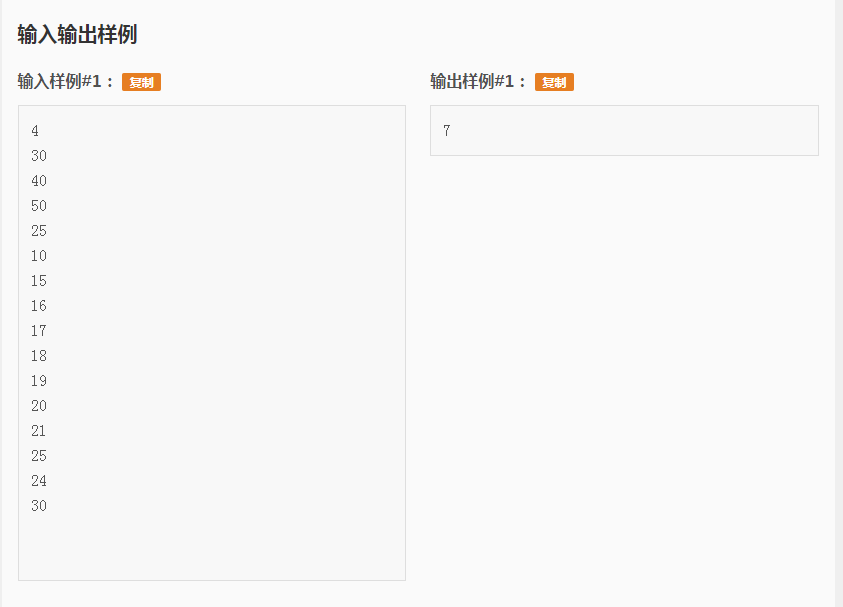
▎题目

题目及测评链接：戳这里

▎前置技能

　　贪心(点击查看)、搜索(点击查看)、剪枝(点击查看)、二分(点击查看)。

▎解析

　　这道题看起来令人不知所措，不知道的东西太多了，到底如何分配，一看就是要用到搜索的题，但怕是连搜索也很难写了。

　　我们按照顺序一点一点的想：

　　首先，我们不知道如何分配，只能像无头苍蝇一样到处乱撞，所以我们可以先假设有多少人可以被满足，然后再实际用搜索检验一下这个假设是否可以成功，如果能行，那么增加这个假设的人数，继续试验；如果不行，那么就减少这个假设的人数，继续试验。

　　这就和原来不一样了，现在是有目标的，而且可以充分保证正确率。现在大致的思路就是这样的：

　　

　　这就是我们的整体大思路，但是这样的方法时间复杂度显然是不可以的，我们需要一定的优化，其实优化是很简单的，只要有点生活常识就行：

　　①一块蛋糕一定能满足更多的嘴小的人，而不是更多嘴大的人。所以，贪心的想：如果将人按照嘴的大小排序，是不是更好呢？

　　②题目中明确规定不能将两块蛋糕拼起来，所以，如果一个人嘴大到连最大的蛋糕都无法满足，那就可以把他踢出去了，那么就不再考虑这个人了，因为无论如何都满足不了。所以依次（从大到小）把嘴大于最大的蛋糕的人全部排除掉，减少搜索判断次数，就可以起到优化的效果了。

　　③我们要先假设能满足的人数，那么该怎样假设呢？总得有个顺序吧，从小到大?从大到小？显然多一次假设就会多一次搜索，那么减少假设次数便是一个关键。于是我们便想到了二分，如果使用二分的话，就可以大大减少假设次数。

　　④剪枝优化1：每一次试探中蛋糕都会有所浪费，怎样判别是否浪费呢？显然，如果一块蛋糕分给一个人一部分后，剩下的连嘴最小的人都满足不了了，那么就一定浪费了。如果蛋糕总量减去浪费的蛋糕量（即这种方法剩下的蛋糕总量）比前n个人的总需求量还小，那么就说明无论如何都满足不了这n个人了，应该立即返回0，表示这种方案失败，换一种方案再继续搜索，这样就会少递归很多次。

　　⑤剪枝优化2：如果前一个人和这个人的嘴一样大，那么就可以优化判断前面的人是否可以被满足，减少for循环次数，由于这个人在第i个蛋糕之前的蛋糕都已经无法满足了（所以才会使用第i个蛋糕来满足），因为前一个人和这个人嘴一样大，所以前i个蛋糕也无法满足这个人了，因此，下一次循环可以特意从当前的i开始循环，而same_start也就是这样起到标记效果的。

▎Code speaks louder than words!

　　废话不多说了，详细的地方都已经写好了注释，直接上代码吧！

---

 #include<iostream>
 #include<algorithm>
 #define bug cout<<"no error!";
 using namespace std;
 int mouth[],cake[],c[],pre[],waste,all,n,m,l,r,mid,ans,maxn;//变量的意思（依次）
 //嘴的大小、蛋糕的大小、蛋糕大小副本、前缀和、浪费值、蛋糕总体积 、蛋糕个数、嘴的个数、二分左边界、右边界
 //二分的中点、答案、最大的蛋糕的体积
 int dfs(int num,int same_start)//num表示剩下的要满足的人数，同时也巧妙的表示了人嘴的编号
 //same_start未剪枝时都可以当做1，而在进行剪枝时的用处详见上文
 {
     if(num==) return ;//能够分配完所有的人，那么返回1
     if(all-waste<pre[mid]) return ;//剪枝优化1，详见上文
     for(int i=same_start;i<=n;i++)
     {
         if(c[i]>=mouth[num])
         {
             c[i]-=mouth[num];//如果能满足这个人，那么就让他吃掉，进行试探
             if(c[i]<mouth[]) waste+=c[i];//如果连口最小的人都满足不了，
             //那么只能浪费,于是增加浪费值，便于上面的剪枝
             if(mouth[num]==mouth[num-])//剪枝优化2，详见上文
             {
                 if(dfs(num-,i)) return ;
             }
             else if(dfs(num-,)) return ;
             if(c[i]<mouth[]) waste-=c[i];//回溯
             c[i]+=mouth[num];//回溯
         }
     }
     return ;//如果是可以满足的，那么上面会返回的，否则就是不可以满足，返回0
 }
 int main()
 {
     cin>>n;
     for(int i=;i<=n;i++)
     {
         cin>>cake[i];
         all+=cake[i];//记录蛋糕总量，用于剪枝
         if(cake[i]>maxn) maxn=cake[i];//记录最大的蛋糕大小，后面有用
     }
     cin>>m;
     for(int i=;i<=m;i++)
     cin>>mouth[i];
     sort(mouth+,mouth+m+);//贪心：将每个人按嘴的大小排序
     while(maxn<mouth[m]) m--;//从嘴最大的人开始，如果嘴比最大的蛋糕还大，那么一定无法满足
     //因为无法将两块蛋糕拼起来给人
     for(int i=;i<=m;i++)
     pre[i]=pre[i-]+mouth[i];//记录前缀和，用于剪枝
     l=;r=m;//规定好二分查找左右边界
     while(l<=r)
     {
         waste=;//浪费值初始为0
         mid=(l+r)/;
         for(int i=;i<=n;i++) c[i]=cake[i];//如果在搜索中用cake数组的话，可能在没有回溯前就返回了，
         //那样cake值会变，影响下一轮搜索，所以赋值到c数组中，使用c数组代替，就像是常说的副本一样
         if(dfs(mid,))
         {
             ans=mid;//如果这个猜测能完成，那么就要记录下答案，不停覆盖，直到最后找到
             l=mid+;
         }
         else r=mid-;//注意：这里千万不要写成r=mid，
         //因为当l=r时，mid=l=r，如果r=mid，那么就会陷入死循环，可以自己模拟一下，l会永远等于r
         //这种情况不可能r<l，所以会一直循环
         //或者这里写成r=mid，但是while的小括号里必须换一个判定条件：l<r也是可以的
     }
     cout<<ans;
     return ;
 }