用Canvas实现Photoshop的钢笔工具（贝塞尔曲线）
前两天在用Canvas实现一个绘制路径的小功能。做完之后发现加以完善可以“复刻”一下PS里面的钢笔工具。
PS里的钢笔工具对我来说是PS中最好用的工具！
所以本文主要介绍如何用Canvas来实现Photoshop中的钢笔工具
需求分析
首先我们来分析一下需求。
1、在画布上的点击效果
1.1点击可生成方形锚点
1.2锚点数量>=2时开始绘制路径
1.3绘制完成的锚点再次点击可进行删除
1.4第一次点击初始锚点可闭合路径（当然以后再点击就是删除路径啦）
2、点击锚点同时按住键盘按键（这里的按键主要是Ctrl键和Alt键）
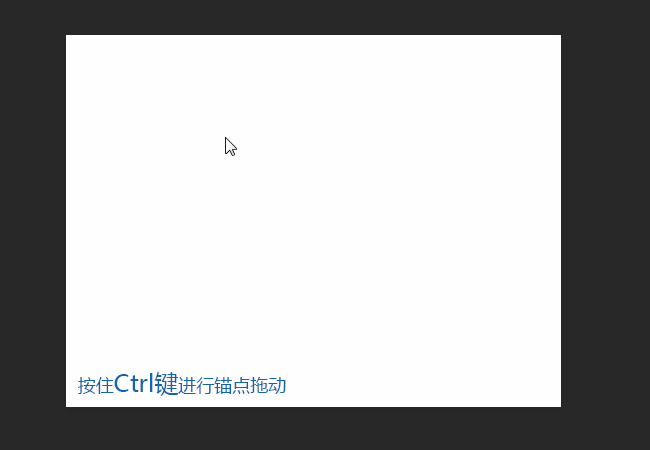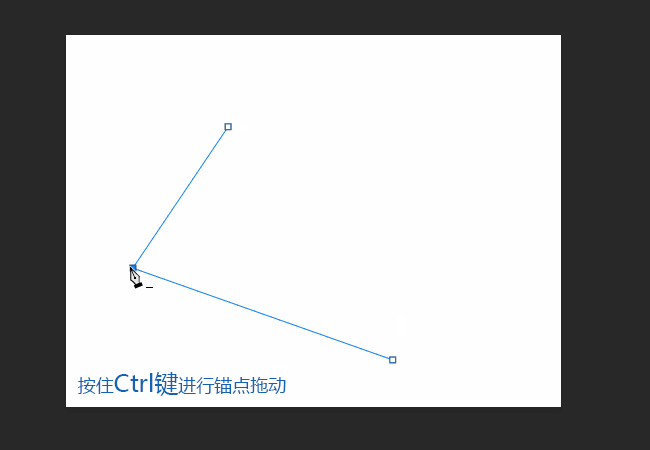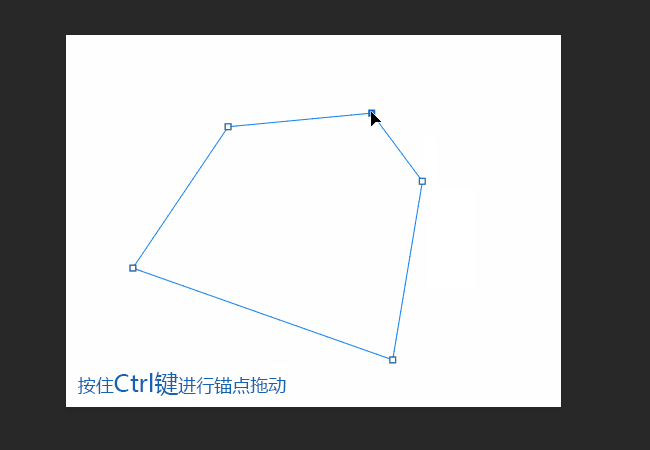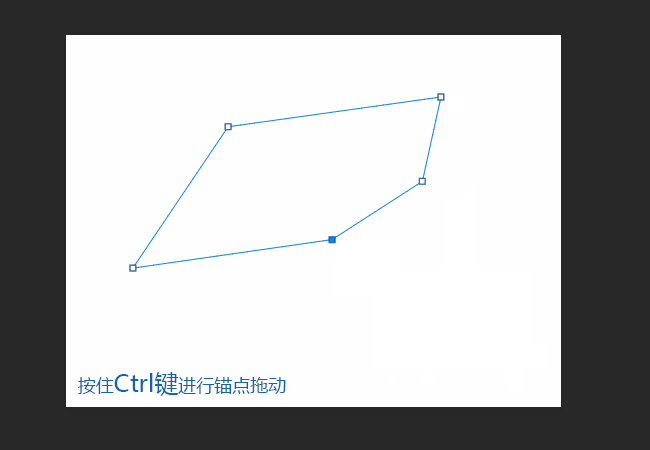
2.1点击方形锚点并按住Ctrl键可对锚点进行拖动
2.2点击方形锚点并按住Alt键可在对应锚点周围生成小圆点，此时移动鼠标会绘制小圆点与方形锚点形成的一条直线路径，长度由鼠标拖动进行控制
2.2.1拖动小圆点可变换弧形路径
3、总体功能使用与功能捡漏
2.2.2点击小圆点并按住Alt键可同时改变两个锚点的角度与长度，此时两个小圆点与方形锚点永远在一条直线上
2.2.3点击小圆点并按住Ctrl键可单独改变一个锚点的角度与长度，另一个小圆点不受影响
功能实现
首先要实现一个钢笔的工具，我们要有点击区域，而且这个点击区域必须是与Canvas重合的，这样才能获取到正确的坐标。
<canvas id="configCan" width="" height=""></canvas><!--canvas绘制区-->
<div id="drawLine">
<div id="clickZone" style="width: 800px;height: 600px;"></div><!--点击区域-->
<div id="point"></div><!--锚点放置区-->
</div>
基础的样式
.mini-box{/*锚点样式*/
width: 10px;
height: 10px;
background-color: #ffffff;
border: 1px solid #1984ec;
position: absolute;
}
.mini-box-down{/*锚点选中样式*/
background-color: #1984ec;
}
.closeP{/*闭合路径鼠标样式*/
cursor:pointer;
}
.delP{/*删除锚点鼠标样式*/
cursor:pointer;
}
.move{
cursor: move;
}
.mini-cir{/*圆点样式*/
position: absolute;
display: inline-block;
width: 10px;
height: 10px;
border: 1px solid #1984ec;
background-color: #ffffff;
border-radius: 5px;
}
.mini-cir-down{/*圆点选中样式*/
background-color: #1984ec;
}
知识点：
cursor：光标的样式属性
border-radius：向DIV添加圆角边框属性
点击区域的事件
$(document).ready(function(){
let currentX1,currentY1;
$("#clickZone").click(function () {
}).mousedown(function (e) {
let length = document.getElementsByClassName("point-can").length;
let poDiv;
currentX1 = e.offsetX;//获取当前鼠标位置
currentY1 = e.offsetY;
if(length){//判断当前是否是第一个锚点
let poCan = document.getElementsByClassName("point-can");
let targetId = parseInt(poCan[(length-1)].id.substring(2));
poDiv = $('<div></div>');
poDiv.attr({"class": "mini-box point-can delP mini-box-down","id":"po"+(targetId+1),"title": "删除锚点"});
let poId = "#po"+targetId;
$(poId).removeClass("mini-box-down");
$(poId).after(poDiv);
}else{
poDiv = $('<div></div>');
poDiv.attr({"class": "mini-box point-can closeP mini-box-down","id":"po1","title": "闭合路径"});
$("#point").html(poDiv);
}
$("#"+poDiv[0].id).css({top:currentY1,left:currentX1});//锚点位置为当前点击位置
drawAll();//注册锚点的事件的方法
});
});
实现方法：
点击后记录当前鼠标的坐标，判断是否是第一个点，然后插入DIV，并为其设置坐标。
知识点：
e事件的offset属性表示原点为触发事件元素的左上角，例如offsetX的数值，即表示点击时，鼠标距离被点击元素左上角原点的x值。
具体可见：offsetX、clientX、screenX、pageX、layerX
锚点的注册事件
var drawAll = function () {
$("#point").css('visibility', 'visible');
drawPath();
let miniBoxs = document.getElementsByClassName("point-can");
let cmove = false;//圆点移动的标志
let flag = false;//锚点移动的标志
let po1State = false;//第一个锚点的状态
let delState = true;//删除状态
let currentX,currentY;//存储当前坐标
let that;//存储锚点状态
$("#drawLine").css("z-index",999);
for (let i = 0; i < miniBoxs.length; i++) {
$("#"+miniBoxs[i].id).off('click').on('click',function (e) {//为每一个锚点注册事件
if(closeP){//判断路径是否闭合
if(po1State === false){//这是第一次点击第一个锚点，此时触发的事件为闭合路径
po1State =true;//修改第一个锚点的状态为true
flag = false;
cmove = false;
return;
}
if(delState){//判断是否删除锚点
if(miniBoxs.length===2){//如果锚点数=2，就不可再删除
return;
}
$("#"+e.currentTarget.id).remove();//删除锚点
let target = parseInt(e.currentTarget.id.substring(2));
$(".cir-can"+target).remove();//删除当前锚点下已存在的圆点
delState = false;
drawPath();//重新绘制路径
}
}
if(miniBoxs.length>1&&delState){//路径未闭合状态
if (e.currentTarget.id ==="po1"){
return;
}else{
$("#"+e.currentTarget.id).remove();
let target = parseInt(e.currentTarget.id.substring(2));
$(".cir-can"+target).remove();
delState = false;
drawPath();
}
}
}).off('mousedown').on('mousedown',function (e) {
cmove = true;
cirChange = true;//设置圆点改变状态为true，表示此时圆点的状态已经改变
$(".mini-cir").removeClass("mini-cir-down");
that = null;
if(window.event.ctrlKey) {//点击锚点并按住ctrl键
delState = false; //设置删除状态为false
flag = true;//移动标志
that = e;
}else{
delState = true;
}
if(window.event.altKey){//点击锚点并按住alt键
that = e;
}
if(that===null){
that = e;
}
$("#"+e.target.id).addClass("mini-box-down");
currentX = e.pageX - parseInt($("#"+e.currentTarget.id).css("left"));
currentY = e.pageY - parseInt($("#"+e.currentTarget.id).css("top"));
if(e.currentTarget.id === "po1"&&!po1State){//第一次点击 第一个生成的锚点，闭合路径
closeP = true; //设置闭合路径的状态为true
$("#po1").removeClass("closeP");
$("#po1").addClass("mini-box-down delP");
$("#po1").removeAttr("title");
$("#po1").attr("title","删除锚点");
$("#po"+miniBoxs.length).removeClass("mini-box-down");//移除上一个锚点的选中状态
drawPath();
}
}).off('mouseup').on('mouseup',function (e) {
flag = false;
cmove = false;
that = null;
});
}
$("#drawLine").on('mousemove',function (e) {
let targetId;
if(that){//获取当前点击的锚点ID
targetId = "#"+that.target.id;
}
if(window.event.ctrlKey&&flag&&that) {
delState = false;
if (flag) {
var x = e.pageX - currentX;//移动时根据鼠标位置计算控件左上角的绝对位置
var y = e.pageY - currentY;
$(targetId).css({top: y, left: x});//控件新位置
$(targetId).addClass("mini-box-down");//添加选中状态
let target = parseInt(that.target.id.substring(2));
var cir = document.getElementsByClassName("cir-can"+target);
if(cir.length){
if(cirChange){//判断与上次相比，圆点是否发生变化
cir1X = cir[0].offsetLeft - x;
cir1Y = cir[0].offsetTop - y;
cir2X = cir[1].offsetLeft - x;
cir2Y = cir[1].offsetTop - y;
}
if(cir1X){
$(cir[0]).css({top:y+cir1Y,left:x+cir1X});
$(cir[1]).css({top:y+cir2Y,left:x+cir2X});
}else{
$(cir[0]).css({top:(y),left:(x)});
$(cir[1]).css({top:(y),left:(x)});
}
}
drawPath();
cirChange = false;
}
return;
}
if(window.event.altKey&&cmove&&that){//点击锚点并按住alt键
delState = false;
$(targetId).addClass("mini-box-down");
let target = parseInt(that.target.id.substring(2));
let cirCans = document.getElementsByClassName("cir-can"+target);
if(!cirCans.length){//判断圆点是否存在，否则创建
let cirs = [];
let cirDiv1 = $('<div></div>');
cirDiv1.attr({"class": "mini-cir cir-can"+target,"id":"cir"+(2*target-1)});
cirs.push(cirDiv1);
let cirDiv2 = $('<div></div>');
cirDiv2.attr({"class": "mini-cir cir-can"+target,"id":"cir"+(target*2)});
cirs.push(cirDiv2);
$("#"+that.target.id).after(cirs);
drawCir();
}
let x = e.pageX - currentX;//移动时根据鼠标位置计算控件左上角的绝对位置
let y = e.pageY - currentY;
$("#cir"+(target*2-1)).css({left:x,top:y});//根据鼠标位置改变奇数圆点即此锚点的第一个圆点坐标
$("#cir"+(target*2-1)).addClass("mini-cir-down");
let po = document.getElementById("po"+target);
let X = x - parseInt(po.offsetLeft);
let Y = y - parseInt(po.offsetTop);
$("#cir"+target*2).css({left:(po.offsetLeft-X),top:(po.offsetTop-Y)});
drawPath();
return;
}
that = null;
});
};
实现方法：
点击锚点（即小方块）判断删除状态delState，判断是否删除锚点。（点击并按下按键使delState为false）
由于第一个锚点是判断路径是否闭合的关键锚点，所以设置po1State，来记录状态，当第一次点击时，设置锚点状态为true，此时路径已闭合，此锚点也成为普通锚点可进行删除操作。
按住ctrl键时可拖动锚点的位置，这个时候需要注意记录此锚点是否存在圆点，要获取圆点的坐标一并进行移动。
此时需要注意与圆点的移动进行关联，当圆点位置改变时，需记录状态，更新圆点的坐标。
按住alt键可生成/移动圆点坐标，移动的是当前锚点的第一个圆点的坐标（也就是奇数圆点的坐标），另一个圆点（偶数圆点）的坐标根据第一个圆点的坐标进行设置，保证此时两个圆点与锚点永远在一条直线上，并且两个圆点距离锚点的距离相同。
知识点：
获取当前按键是否按下使用window.event.altKey、window.event.ctrlKey属性来进行判断。
圆点的注册事件
var drawCir = function () {//圆点的事件注册
let miniCirs = document.getElementsByClassName("mini-cir");
let ccurrentX,ccurrentY;
let cthat = null;
let changeId;//记录当前圆点是否发生变化
let targetId = 0;
for (let i = 0; i < miniCirs.length; i++) {
$("#"+miniCirs[i].id).off('click').on('click',function (e) {
cFlag = false;
$(".mini-cir").removeClass("mini-cir-down");//移除所有选中状态
}).off('mousedown').on('mousedown',function (e) {
cFlag = true;//圆点移动标记
if(cthat===null){
cthat = e;
}
ccurrentX = e.pageX - parseInt($("#"+e.currentTarget.id).css("left"));
ccurrentY = e.pageY - parseInt($("#"+e.currentTarget.id).css("top"));
targetId = parseInt(e.target.id.substring(3));
});
}
$("#drawLine").on('mousemove',function (e) {
if (cFlag) {
if(cthat===null){
return;
}
if(window.event.altKey&&cthat){//点击圆点并按下alt键
let x = e.pageX - ccurrentX;//移动时根据鼠标位置计算控件左上角的绝对位置
let y = e.pageY - ccurrentY;
$("#"+cthat.target.id).css({top: y, left: x});//选中圆点的新位置
$("#"+cthat.target.id).addClass("mini-cir-down");//添加选中状态
let ctarget = targetId;//获取当前点击的圆点ID
let po,cX,cY;
if(ctarget%2){//根据圆点ID获取与其成对的另一个圆点的坐标
po = document.getElementById("po"+(ctarget+1)/2);
cX = parseInt($("#cir"+(ctarget+1)).css('left')) - parseInt($("#po"+(ctarget+1)/2).css('left'));
cY = parseInt($("#cir"+(ctarget+1)).css('top')) - parseInt($("#po"+(ctarget+1)/2).css('top'));
changeId = ctarget+1;
}else{
po = document.getElementById("po"+ctarget/2);
cX = parseInt($("#cir"+(ctarget-1)).css('left')) - parseInt($("#po"+ctarget/2).css('left'));
cY = parseInt($("#cir"+(ctarget-1)).css('top')) - parseInt($("#po"+ctarget/2).css('top'));
changeId = ctarget-1;
}
let X = parseInt(cthat.target.offsetLeft) - parseInt(po.offsetLeft);//当前点击圆点与锚点的距离
let Y = parseInt(cthat.target.offsetTop) - parseInt(po.offsetTop);
let sLength = Math.sqrt(X*X + Y*Y);//计算当前圆点与锚点的长度
if(cId === null){
cId = ctarget;
}
if(cId !== ctarget){//判断当前的圆点ID是否发生变化来确定是否重新计算成对圆点的长度
cId = ctarget;
cIdChange = true;
}else{
cIdChange = false;
}
if(cLength===0||cIdChange){
cLength = parseInt(Math.sqrt(cX*cX + cY*cY));//计算与当前点击圆点成对的另一个圆点与锚点的长度
}
let mul1 = (X/sLength).toFixed(2);//省略小数以减小误差
let mul2 = (Y/sLength).toFixed(2);
if(X>0){//根据当前圆点相对于锚点的位置设置与之对应的圆点的坐标，使得当前圆点与对应圆点永远在一条直线上
if(mul2<0){
$("#cir"+changeId).css({top:(po.offsetTop-(cLength*mul2)),left:(po.offsetLeft-(cLength*mul1))});
}else{
$("#cir"+changeId).css({top:(po.offsetTop-(cLength*mul2)),left:(po.offsetLeft-(cLength*mul1))});
}
}else{
if(mul2<0){
$("#cir"+changeId).css({top:(po.offsetTop-(cLength*mul2)),left:(po.offsetLeft-(cLength*mul1))});
}else{
$("#cir"+changeId).css({top:(po.offsetTop-(cLength*mul2)),left:(po.offsetLeft-(cLength*mul1))});
}
}
}
if(window.event.ctrlKey&&cthat){//点击圆点并按住ctrl键
let target = parseInt(cthat.target.id.substring(3));
$(".mini-cir").removeClass("mini-cir-down");
let x = e.pageX - ccurrentX;//移动时根据鼠标位置计算控件左上角的绝对位置
let y = e.pageY - ccurrentY;
$("#cir"+target).css({left:x,top:y});//此时只改变当前圆点的坐标
$("#cir"+target).addClass("mini-cir-down");
}
drawPath();
}
}).off('mouseup').on('mouseup',function (e) {
cthat = null;
cFlag = false;
});
};
实现方法：
点击圆点并按住Alt键可对当前圆点进行拖动，此时另一个圆点也随之改变，永远与当前锚点，当前圆点三点连成一条直线。
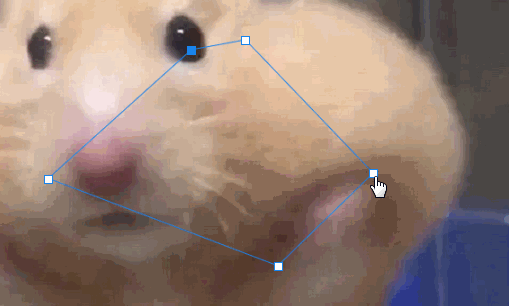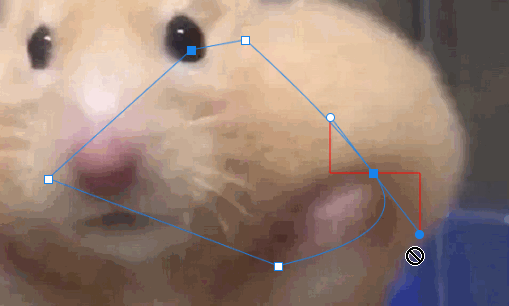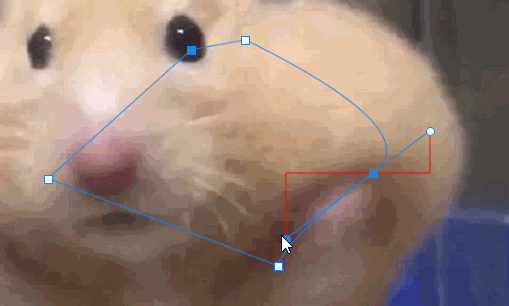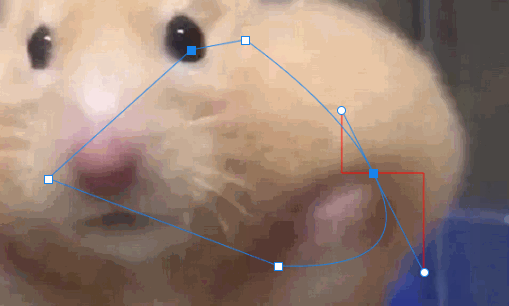
其中，当按住Alt键移动当前圆点时，另一个圆点与锚点的长度不变，所以需要记录鼠标按下状态时，另一圆点的坐标，根据坐标计算长度。
如图所示，两个圆点与锚点呈相似三角形，所以当鼠标松开时，根据此时圆点与锚点的角度，可以计算另一圆点的坐标。
点击圆点并按住Ctrl键可对当前圆点进行拖动，此时仅改变当前点击圆点的坐标，不对另一个圆点造成影响。
知识点：
Math.sqrt()：可返回一个数的平方根。
toFixed(num)：把数字四舍五入为指定小数位数num的数字。
绘制路径方法
var poPositions = [];
var drawPath = function () { let configCan = document.getElementById("configCan");
let ctx = configCan.getContext("2d");
ctx.clearRect(0, 0, 800, 600);//清空画布
let poCan = document.getElementsByClassName("point-can");
poPositions = [];
for(let i = 0;i<poCan.length;i++){
let position = {x:0,y:0};
position.x = poCan[i].offsetLeft + 4;
position.y = poCan[i].offsetTop + 4;
poPositions.push(position);
}//获取锚点坐标
let cirCanP = [];
for(let i = 0;i<poCan.length;i++){
let targetId = parseInt(poCan[i].id.substring(2));
let cir = document.getElementsByClassName("cir-can"+targetId);
let cirP ;
if(cir.length){
cirP = [];
for(let j = 0;j<2;j++){
let position = {x:0,y:0};
position.x = cir[j].offsetLeft + 4;
position.y = cir[j].offsetTop + 4;
cirP.push(position);
}
}
cirCanP[i] = cirP;
}//获取圆点坐标
for(let i = 0;i<poPositions.length;i++){
if(poPositions[i]&&cirCanP[i]){
ctx.beginPath();
ctx.strokeStyle = "#1984ec";
ctx.moveTo(cirCanP[i][0].x,cirCanP[i][0].y);
ctx.lineTo(poPositions[i].x,poPositions[i].y);
ctx.lineTo(cirCanP[i][1].x,cirCanP[i][1].y);
ctx.stroke();
}
}//绘制已存在圆点与其对应锚点的直线
ctx.beginPath();
ctx.strokeStyle = "#1984ec";
ctx.moveTo(poPositions[0].x, poPositions[0].y);
if(cirCanP[0]){//如果第一个锚点的圆点存在
if(!cirCanP[1]){//且第二个锚点的圆点不存在，则绘制二次贝塞尔曲线
ctx.quadraticCurveTo(cirCanP[0][1].x,cirCanP[0][1].y,poPositions[1].x,poPositions[1].y);
}else{//且第二个锚点的圆点存在，则绘制三次贝塞尔曲线
ctx.bezierCurveTo(cirCanP[0][1].x, cirCanP[0][1].y, cirCanP[1][0].x,cirCanP[1][0].y, poPositions[1].x, poPositions[1].y);
}
for(let i = 1;i<poPositions.length;i++){
if(i===(poCan.length-1)){
if(cirCanP[i]){//如果最后一个锚点的圆点存在
if(cirCanP[(i-1)]){//且倒数第二个锚点的圆点存在，则绘制三次贝塞尔曲线
ctx.bezierCurveTo(cirCanP[i][1].x, cirCanP[i][1].y, cirCanP[0][0].x,cirCanP[0][0].y, poPositions[0].x, poPositions[0].y);
ctx.stroke();
return;
}else{//且倒数第二个锚点不存在
ctx.quadraticCurveTo(cirCanP[i][0].x,cirCanP[i][0].y,poPositions[i].x, poPositions[i].y);//先绘制倒数第二个锚点与倒数第三个点的二次贝塞尔曲线
ctx.bezierCurveTo(cirCanP[i][1].x, cirCanP[i][1].y, cirCanP[0][0].x,cirCanP[0][0].y, poPositions[0].x, poPositions[0].y);//再绘制最后一个锚点与第一个锚点的三次贝塞尔曲线
ctx.stroke();
return;
} }else{//如果最后一个锚点不存在
if(cirCanP[(i-1)]){//且倒数第二个锚点存在，则绘制第一个锚点与最后一个锚点的二次贝塞尔曲线
ctx.quadraticCurveTo(cirCanP[0][0].x,cirCanP[0][0].y,poPositions[0].x, poPositions[0].y);
ctx.stroke();
return;
}else{//且倒数第二个锚点不存在
ctx.lineTo(poPositions[i-1].x, poPositions[i-1].y);//绘制第二个锚点
ctx.lineTo(poPositions[i].x, poPositions[i].y);//绘制最后一个锚点
ctx.quadraticCurveTo(cirCanP[0][0].x,cirCanP[0][0].y,poPositions[0].x, poPositions[0].y);//绘制最后一个锚点到第一个锚点的二次贝塞尔曲线
ctx.stroke();
return;
}
}
}
if(cirCanP[i]){//如果当前锚点存在小圆点
if(cirCanP[i-1]){//且前一个锚点小圆点存在
if(cirCanP[i+1]){//且后一个锚点小圆点存在
ctx.bezierCurveTo(cirCanP[i][1].x, cirCanP[i][1].y, cirCanP[i+1][0].x,cirCanP[i+1][0].y, poPositions[i+1].x, poPositions[i+1].y);//绘制当前锚点与下一个锚点的三次贝塞尔曲线
}else{//且后一个锚点小圆点不存在
ctx.quadraticCurveTo(cirCanP[i][1].x, cirCanP[i][1].y, poPositions[i+1].x, poPositions[i+1].y);//绘制当前锚点与下一个锚点的二次贝塞尔曲线
}
}else if(cirCanP[i+1]){//且后一个锚点小圆点存在，此时前一个锚点不存在小圆点
ctx.quadraticCurveTo(cirCanP[i][0].x, cirCanP[i][0].y, poPositions[i].x, poPositions[i].y);//则绘制前一个锚点与当前锚点的二次贝塞尔曲线
ctx.bezierCurveTo(cirCanP[i][1].x, cirCanP[i][1].y, cirCanP[i+1][0].x,cirCanP[i+1][0].y, poPositions[i+1].x, poPositions[i+1].y);//绘制当前锚点与后一个锚点的三次贝塞尔曲线
}else{//前一个锚点与后一个锚点都不存在小圆点
ctx.quadraticCurveTo(cirCanP[i][0].x, cirCanP[i][0].y, poPositions[i].x, poPositions[i].y);//绘制前一个锚点的与当前锚点的二次贝塞尔曲线
ctx.quadraticCurveTo(cirCanP[i][1].x, cirCanP[i][1].y, poPositions[i+1].x, poPositions[i+1].y);//绘制当前锚点与后一个锚点的二次贝塞尔曲线
}
}else{//如果当前锚点不存在小圆点
ctx.lineTo(poPositions[i].x, poPositions[i].y);//则绘制当前锚点
}
}
}else{//第一个锚点的小圆点不存在的情况，其余同上
for(let i = 1;i<poPositions.length;i++){
if(i===(poCan.length-1)){
if(cirCanP[i]){
if(cirCanP[i-1]){
ctx.quadraticCurveTo(cirCanP[i][1].x,cirCanP[i][1].y,poPositions[0].x, poPositions[0].y);
ctx.stroke();
return;
}else{
ctx.lineTo(poPositions[i-1].x, poPositions[i-1].y);
ctx.quadraticCurveTo(cirCanP[i][0].x,cirCanP[i][0].y,poPositions[i].x, poPositions[i].y);
ctx.quadraticCurveTo(cirCanP[i][1].x,cirCanP[i][1].y,poPositions[0].x, poPositions[0].y);
ctx.stroke();
return;
}
}
}
if(cirCanP[i]){
if(cirCanP[i-1]){
if(cirCanP[i+1]){
ctx.bezierCurveTo(cirCanP[i][1].x, cirCanP[i][1].y, cirCanP[i+1][0].x,cirCanP[i+1][0].y, poPositions[i+1].x, poPositions[i+1].y);
}else{
ctx.quadraticCurveTo(cirCanP[i][1].x, cirCanP[i][1].y, poPositions[i+1].x, poPositions[i+1].y);
} }else if(cirCanP[i+1]){
ctx.quadraticCurveTo(cirCanP[i][0].x, cirCanP[i][0].y, poPositions[i].x, poPositions[i].y);
ctx.bezierCurveTo(cirCanP[i][1].x, cirCanP[i][1].y, cirCanP[i+1][0].x,cirCanP[i+1][0].y, poPositions[i+1].x, poPositions[i+1].y);
}else{
ctx.quadraticCurveTo(cirCanP[i][0].x, cirCanP[i][0].y, poPositions[i].x, poPositions[i].y);
ctx.quadraticCurveTo(cirCanP[i][1].x, cirCanP[i][1].y, poPositions[i+1].x, poPositions[i+1].y);
}
}else{
ctx.lineTo(poPositions[i].x, poPositions[i].y);
} }
}
if(closeP){//如果闭合路径状态为true，则闭合路径
ctx.closePath();
}
ctx.stroke();
};
实现方法：
获取锚点坐标，并获取对应的圆点坐标，分别存在数组中。
绘制圆点与锚点的直线，根据圆点数量判断锚点绘制直线、二次贝塞尔曲线、三次贝塞尔曲线。
知识点：
Canvas方法/属性：
clearRect(x,y,width,height)：清除画布，x、y表示开始清除的坐标，width、height表示清除的区域。
beginPath()：画布中开始子路径的一个新的集合，建议每次开始画一个子路径的时候都显示地调用，不然会出行路径粘连。
strokeStyle属性：笔触颜色，可选值为颜色、渐变、图案
（与上面相对的是fillStyle属性：填充颜色，可选值也为颜色、渐变、图案）
moveTo(x,y)：开始绘制的第一个点坐标
lineTo(x,y)：创建下一个点坐标
closePath()：将最后一个点与第一个点相连
注：以上三个方法并没有绘制路径，只是确定了坐标
stroke()：绘制路径，这个方法才真正将坐标点相连绘制了路径
绘制曲线最重要的知识点就是就是贝塞尔曲线。
贝塞尔曲线的知识介绍参考这个链接：Canvas学习：贝塞尔曲线
这里我就简单讲一下我自己的理解。
大体上，PS中的曲线分为两种，一种普通曲线，一种高级曲线。普通曲线就是由三点驱动的曲线，这种曲线就一个弧度，要么凸，要么凹。曲线的曲度由中间那个点来控制，绘制时就是贝塞尔二次曲线。
高级曲线就是四点驱动的曲线，这种曲线有波浪的效果，曲线是曲度由两个点来控制，所以可以实现S型曲线，也就是两个弧度的曲线，绘制时就是贝塞尔三次曲线。
绘制贝塞尔曲线时，需要使用moveTo(x,y)方法显示指定第一个点的坐标。
quadraticCurveTo(cx,cy,x,y)：绘制贝塞尔二次曲线，cx，cy就是中间那个控制点，表现为那个小圆点，x，y就是相邻锚点的坐标。
bezierCurveTo(c1x,c1y,c2x,c2y,x,y)：绘制贝塞尔三次曲线，c1x，c1y就是前一个锚点的第二个小圆点坐标，c2x，c2y就是后一个锚点的第一个小圆点坐标，x，y就是后一个锚点的坐标。
理清楚这些，整体实现起来就很快啦！
以上就是实现Photoshop钢笔工具的全部代码和部分讲解，来看看最终实现效果。
不足：没有实现PS中创建锚点时拖动鼠标就生成小圆点的效果，也没有删除圆点坐标的操作，只能无限接近锚点坐标。
方法写得乱七八糟，JQ和原生JS混乱使用。
改进：根据我自己的使用习惯，在点击小圆点按住Ctrl键改变坐标，使两个点不在一条直线上后，再按住Alt键可使两个点重新恢复到一条直线上。PS中的话，就无法恢复到一条直线了，除非重新生成圆点坐标。
后续还会继续进行修改！
源码地址：https://github.com/Chellyyy/Canvas_PS_PenTool
用Canvas实现Photoshop的钢笔工具（贝塞尔曲线）的更多相关文章
- canvas贝塞尔曲线
贝塞尔曲线 Bézier curve(贝塞尔曲线)是应用于二维图形应用程序的数学曲线. 曲线定义:起始点.终止点.控制点.通过调整控制点,贝塞尔曲线的形状会发生变化. 1962年,法国数学家Pierr ...
- canvas绘制二次贝塞尔曲线----演示二次贝塞尔四个参数的作用
canvas中绘制二次贝塞尔曲线的方法为ctx.quadraticCurveTo(x1,y1,x2,y2); 四个参数分别为两个控制点的坐标.开始点即当前canvas中目前的点,如果想从指定的点开始, ...
- 关于photoshop钢笔工具中各点对应到“贝塞尔曲线”中的含义（cocos2d-x与iOS）
1.程序中贝塞尔曲线的简单介绍,只介绍曲线部分.程序中的贝塞尔曲线需要四个点:起始点(startPoint) ,控制点1(controlPoint1),控制点2(controlPoint2),结束点( ...
- Canvas中绘制贝塞尔曲线
① 什么是贝塞尔曲线? 在数学的数值分析领域中,贝济埃曲线(英语:Bézier curve,亦作“贝塞尔”)是计算机图形学中相当重要的参数曲线.更高维度的广泛化贝济埃曲线就称作贝济埃曲面,其中贝济埃三 ...
- 用html5的canvas画布绘制贝塞尔曲线
查看效果:http://keleyi.com/keleyi/phtml/html5/7.htm 完整代码: <!DOCTYPE html PUBLIC "-//W3C//DTD XHT ...
- canvas绘制贝塞尔曲线
原文:canvas绘制贝塞尔曲线 1.绘制二次方贝塞尔曲线 quadraticCurveTo(cp1x,cp1y,x,y); 其中参数cp1x和cp1y是控制点的坐标,x和y是终点坐标 数学公式表示如 ...
- JavaScript+canvas 利用贝塞尔曲线绘制曲线
效果图: <body> <canvas id="test" width="800" height="300">< ...
- [js高手之路] html5 canvas系列教程 - arcTo(弧度与二次,三次贝塞尔曲线以及在线工具)
之前,我写了一个arc函数的用法:[js高手之路] html5 canvas系列教程 - arc绘制曲线图形(曲线,弧线,圆形). arcTo: cxt.arcTo( cx, cy, x2, y2, ...
- 贝塞尔曲线与CSS3动画、SVG和canvas的应用
简介 贝塞尔曲线是可以做出很多复杂的效果来的,比如弹跳球的复杂动画效果,首先加速下降,停止,然后弹起时逐渐减速的效果. 使用贝塞尔曲线常用的两个网址如下: 缓动函数:http://www.xuanfe ...
随机推荐
- Spring的注解问题
Annotation(注解)概述 从JDK5.0开始, Java增加了对元数据(MetaData)的支持,也就是 Annotation(注解). Annotation其实就是代码里的特殊标记,它用于替 ...
- LINUX下查找大文件及大的文件夹
原帖地址:https://www.cnblogs.com/iyoume2008/p/6105590.html 今天正好碰到这样的问题,在博客园中看到有以上地址的一篇文章,照着上面的操作解决了问题,但是 ...
- Apache Httpd 启用重定向 rewrite
1.启用模块 由:#LoadModule rewrite_module modules/mod_rewrite.so 更改为:LoadModule rewrite_module modules/mod ...
- 实战SpringCloud响应式微服务系列教程（第一章）
前言 在当今互联网飞速发展的时代,业务需求不断的更新和产品的迭代给系统开发过程和编程模式也带来巨大挑战,Spring Cloud微服务也随之应用而生,从springboot1.x到springboot ...
- textarea的拖拽怎么解决
textarea文本域在页面中是可以拖动的,即时你给了固定的宽度和高度,但这在我们页面布局中,使我们不需要的,因为可拖拽很多时候会影响我们页面的布局和整体的美观度. css3提供了一个resize属性 ...
- IDEA下基于MAVEN的SSM框架整合
源码可以以上传github https://github.com/ingxx/ssm_first 最近把用IDEA把SSM框架整合一遍遇到了不少坑,在这里写出来 这里maven我使用的是自己下载的3. ...
- python 的几种数据类型
列表 列表是 Python 的主力数据类型.当提到 " 列表 " 时,您脑海中可 能会闪现" 必须进一步声明大小的数组,只能包含同一类对象 " 等想法.千 ...
- poj 1068 模拟
题目链接 大概题意就是告诉你有个n个小括号,每一个")"左边有多少个"("都告诉你了,然后让你求出每一对括号之间有多少对括号(包含自己本身). 思路: 我先计算 ...
- Ubuntu中修改默认开机项
1首先,按住Ctrl+Alt+t打开终端 2输入cd /etc/default 3输入sudo sudo nano grub 并按照提示输入密码 4在我们开机的时候,可以看到自己想要默认的开机项是多少 ...
- RabbitMQ（四）：使用Docker构建RabbitMQ高可用负载均衡集群
本文使用Docker搭建RabbitMQ集群,然后使用HAProxy做负载均衡,最后使用KeepAlived实现集群高可用,从而搭建起来一个完成了RabbitMQ高可用负载均衡集群.受限于自身条件,本 ...