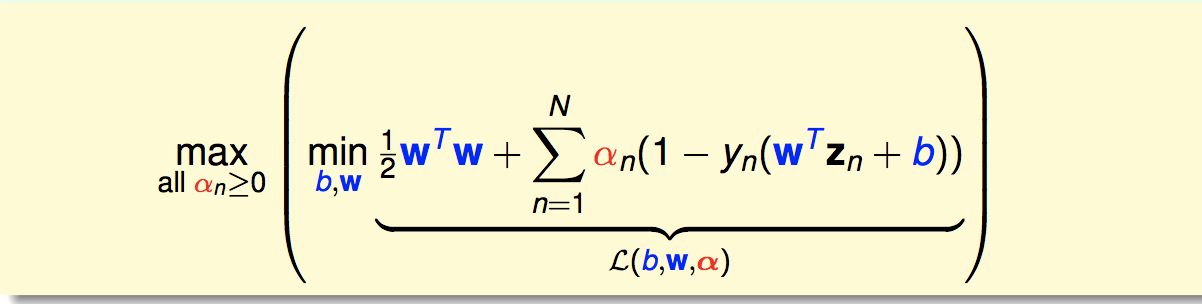《机器学习技法》---对偶SVM
1.对偶问题的推导
为什么要求解对偶问题?一是对偶问题往往更容易求解,二是可以自然的引入核函数。
1.1 用拉格朗日函数将原问题转化为“无约束”等价问题
原问题是:

写出它的拉格朗日函数:

然后我们的原问题就等价为:

为什么可以这样等价:

即:对于不满足约束条件的(b,w),min里面趋于无穷大,因此min就把这些b,w舍去了;对于满足约束条件的解,min里面就刚好是原来的目标函数,刚好与原问题等价。
1.2 导出拉格朗日对偶问题
首先我们有如下成立:

然后我们取右边式子中的“best”阿尔法,仍然会有大于等于号成立,因为best is one of any:

这时右边的式子就是对偶问题。这里直接给出一个定理,当满足下面条件时(对于SVM来说刚好满足),原始问题和对偶问题的解是相同的:

并且它们的最优解满足KKT条件:偏导为0,对偶互补,拉格朗日乘子大于0.
1.3 用KKT条件来简化对偶问题
我们的对偶问题现在是:
根据KKT条件,我们有:

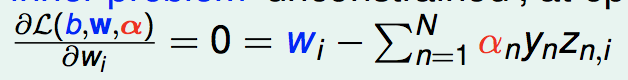
把第一个代进来:

再把第二个代进来:

这时候,我们的问题里面就只剩一个参数阿尔法了。再把平方项展开,写的好看一点,就得到了标准的硬间隔SVM对偶问题:

2. 解对偶问题
还是解QP那一套:

之后再求W和b:
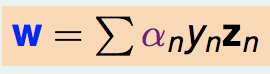 (所有支持向量的加权和)
(所有支持向量的加权和)
 (任取一个支持向量算出)
(任取一个支持向量算出)
3. 支持向量
引出对偶问题后,我们重现定义支持向量为阿尔法大于0的向量。他们一定是在边界上的(统计学习方法p107),但是在边界上的不一定阿尔法大于0:

前面我们也提到过,w和b的计算只需要支持向量,其他向量都是无用的:

《机器学习技法》---对偶SVM的更多相关文章
- 对偶SVM
1.对偶问题的推导 为什么要求解对偶问题?一是对偶问题往往更容易求解,二是可以自然的引入核函数. 1.1 用拉格朗日函数将原问题转化为"无约束"等价问题 原问题是: 写出它的拉格朗 ...
- SVM原理与实践
SVM迅速发展和完善,在解决小样本.非线性及高维模式识别问题中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中.从此迅速的发展起来,已经在许多领域(生物信息学,文本和手写识别等)都取 ...
- SVM1 线性SVM
一.Linear Support Vector Machine 接下来的讨论假设数据都是线性可分的. 1.1 SVM的引入:增大对测量误差的容忍度 假设有训练数据和分类曲线如下图所示: 很明显,三个分 ...
- SVM学习笔记
一.SVM概述 支持向量机(support vector machine)是一系列的监督学习算法,能用于分类.回归分析.原本的SVM是个二分类算法,通过引入“OVO”或者“OVR”可以扩展到多分类问题 ...
- SVM对偶形式
dual svm 对偶SVM linear SVM 可以用二次规划方法解 xn通过非线性转换变成zn SVM配合非线性特征转换 透过large-margin降低模型复杂度 透过特征转换得到弯弯曲曲的边 ...
- SVM笔记
1.前言 SVM(Support Vector Machine)是一种寻求最大分类间隔的机器学习方法,广泛应用于各个领域,许多人把SVM当做首选方法,它也被称之为最优分类器,这是为什么呢?这篇文章将系 ...
- 【机器学习算法基础+实战系列】SVM
概述 支持向量机是一种二分类模型,间隔最大使它有别于感知机.支持向量机学习方法由简至繁的模型:线性可分支持向量机(linear support vector machine in linearly s ...
- SVM小白教程(2):拉格朗日对偶
在上一篇文章中,我们推导出了 SVM 的目标函数: \[ \underset{(\mathbf{w},b)}{\operatorname{min}} ||\mathbf{w}|| \\ \operat ...
- SVM系列之拉格朗日对偶
在学习SVM(Support Vector Machine) 支持向量机时,对于线性可分的分类样本求出的分类函数为: 其中,分类超平面可以表示为:
随机推荐
- Android实现跳转到应用市场进行版本更新功能
最近需要做应用版本更新功能,因为之前已经写过一篇版本更新的功能了,虽然请求接口还是用的HttpUrlConnection,想着改改现在应用使用的请求方式也挺快的嘛,心里开始暗喜,可以偷偷懒了,哈哈哈. ...
- 利用iisnode模块,让你的Node.js应用跑在Windows系统IIS中
最近比较喜欢用Node.js做一些简单的应用,一直想要部署到生产环境中,但是手上只有一台windows server 2008服务器,并且已经开启了IIS服务,运行了很多.Net开发的网站,80端口已 ...
- 宏旺半导体深度剖析嵌入式存储芯片eMMC原理 一篇概括大全
eMMC 一直是嵌入式存储市场最主流的选择,除了读写速度快.性价比高外,在节省空间方面也是相当优秀,今天宏旺半导体就和大家详细聊聊eMMC. eMMC 是 embedded MultiMediaCar ...
- [01] HEVD 双机调试环境搭建
[01] HEVD 双机调试环境搭建 span::selection, .CodeMirror-line > span > span::selection { background: #d ...
- weex起步
weex文档地址: http://weex-project.io/cn/guide/index.html weex的文档过于简单,加上js语法 & android & ios本身也有很 ...
- .net持续集成cake篇之使用vs或者vscode来辅助开发cake脚本
使用Visual Studio来开发工具 前面我们都是通过手写或者复制的方法来编写Cake文件,Cake使用的是C#语言,如果仅使用简单的文本编辑器来编写显然效率是非常低下的,本节我们讲解如何使用ca ...
- RecyclerView下拉加载集合越界问题
问题描述 在做毕业设计app中遇到这样一个问题,使用RecyclerView进行下拉加载数据的时候,比如我每次让它加载5条数据,当服务器端数据总数刚好是5的倍数的时候,不会出现下拉加载数据集合越界的问 ...
- C#中面向对象编程中的函数式编程详解
介绍 使用函数式编程来丰富面向对象编程的想法是陈旧的.将函数编程功能添加到面向对象的语言中会带来面向对象编程设计的好处. 一些旧的和不太老的语言,具有函数式编程和面向对象的编程: 例如,Smallta ...
- 原生 js基础常用的判断和循环
原生 js基础常用的判断和循环 以下部分是个人实践及和搜集的资料: 最常用的if判断语句: if (/* 条件表达式 */){ // 成立执行语句 } else { // 否则执行语句 } 原生js的 ...
- ThreadPoolExecutor带来的性能问题
使用线程池,一般情况下会带来性能提升,并且使用线程池管理线程,减少了每个任务调用的开销,通常可以在执行大量异步任务时提供增强的性能. 但是在高并发的情况下,会因为使用不当导致性能下降,并且下降得比较严 ...