2019 ICPC Asia Nanjing Regional K. Triangle

题目：在直角坐标系中给定 p1,p2,p3构成三角形，给定p4可能在三角形边上也可能不在，

问能不能在三角形上找出p5，使得线段p4p5，平分三角形（p4必须在三角形上）。不能则输出-1.

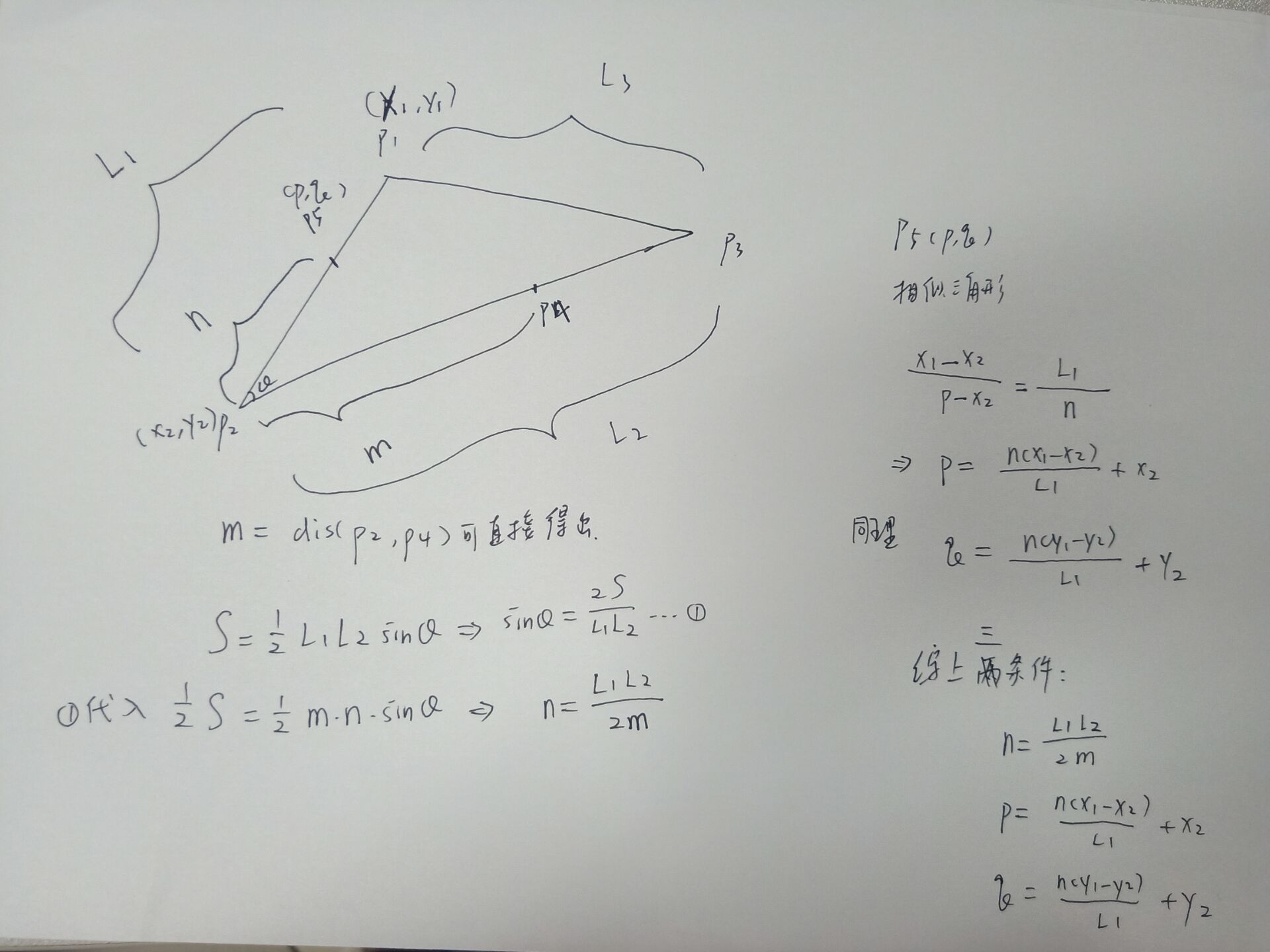
思路：四个点，三条边，三条边的长度，和代码的数据一一对应存储。

①：不在三角形上

②：在三角形上

　　①在顶点上（两条线段上）

　　②不在顶点上（一条线段上）

　　　　①在中点

　　　　②不在中点

最麻烦的就是p4只存在于一条边上。

代码：

 #include<bits/stdc++.h>
 using namespace std;

 const double eps = 1e-;
 int sgn(double x)
 {
     if(fabs(x) < eps)return ;
     if(x < )return -;
     else return ;
 }
 struct Point
 {
     double x,y;
     Point(){}
     Point(double _x,double _y)
     {
         x = _x;y = _y;
     }
     Point operator -(const Point &b)const
     {
         return Point(x - b.x,y - b.y);
     }

     double operator ^(const Point &b)const//叉积
     {
         return x*b.y - y*b.x;
     }

     double operator *(const Point &b)const//点积
     {
         return x*b.x + y*b.y;
     }
     void transXY(double B)//绕原点旋转角度B（弧度值），后x,y的变化
     {
         double tx = x,ty = y;
         x = tx*cos(B) - ty*sin(B);
         y = tx*sin(B) + ty*cos(B);
     }
     void read(double a,double b){
         x = a; y = b;
     }
 };
 struct Line
 {
     Point s,e;
     Line(){}
     Line(Point _s,Point _e)
     {
         s = _s;e = _e;
     }
     pair<int,Point> operator &(const Line &b)const
     {
         //两直线相交求交点
         //第一个值为0表示直线重合，为1表示平行，为0表示相交,为2是相交
         //只有第一个值为2时，交点才有意义
         Point res = s;
         if(sgn((s-e)^(b.s-b.e)) == )
         {
             if(sgn((s-b.e)^(b.s-b.e)) == )
                 return make_pair(,res);//重合
             else return make_pair(,res);//平行
         }
         double t = ((s-b.s)^(b.s-b.e))/((s-e)^(b.s-b.e));
         res.x += (e.x-s.x)*t;
         res.y += (e.y-s.y)*t;
         return make_pair(,res);
     }
     void read(Point& a,Point& b){
         s.x = a.x;
         s.y = a.y;
         e.x = b.x;
         e.y = b.y;
     }
 };
 bool OnSeg(Point& P,Line& L)//判断点在线段上
 {
     return
     sgn((L.s-P)^(L.e-P)) ==  &&
     sgn((P.x - L.s.x) * (P.x - L.e.x)) <=  &&
     sgn((P.y - L.s.y) * (P.y - L.e.y)) <= ;
 }
 //线长
 inline double get_Ldis(Line& L){
     return sqrt((L.s.x-L.e.x)*(L.s.x-L.e.x)+(L.s.y-L.e.y)*(L.s.y-L.e.y));
 }
 //两点长
 inline double get_pdis(Point& a,Point& b){
     return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
 }

 inline void print(Line& L){
     printf("%.12f %.12f\n",(L.s.x+L.e.x)/,(L.s.y+L.e.y)/);
 }

 inline double fun(double n,double x1,double x2,double d){
     return n*(x1-x2)/d + x2;
 }
 Point p[]; Line L[]; double d[];
 inline void solve(Line& l,double m1,double m2,Point& p1,Point& p2,Point& p3,double d1,double d2,double d3){

     double n;
     double x,y;
     if(m1==m2) {printf("%.12f %.12f\n",p1.x,p1.y); return;}
     else if( m1 > m2){
         n = (d1*d2)/(*m1);
         x = fun(n,p1.x,p2.x,d1);
         y = fun(n,p1.y,p2.y,d1);
     }
     else{
         n = (d2*d3)/(*m2);
         x = fun(n,p1.x,p3.x,d3);
         y = fun(n,p1.y,p3.y,d3);
     }
     printf("%.12f %.12f\n",x,y);
 }

 int main()
 {

     int T;
     double m1,m2;
     scanf("%d",&T);
     while(T--){
         scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&p[].x,&p[].y,&p[].x,&p[].y,&p[].x,&p[].y,&p[].x,&p[].y);
         L[].read(p[],p[]); L[].read(p[],p[]); L[].read(p[],p[]);
         for(int i = ; i <= ; ++i) d[i] = get_Ldis(L[i]);

         if(OnSeg(p[],L[]) || OnSeg(p[],L[]) || OnSeg(p[],L[])){
             if(OnSeg(p[],L[]) && OnSeg(p[],L[])){
                 print(L[]); continue;
             }
             if(OnSeg(p[],L[]) && OnSeg(p[],L[])){
                 print(L[]);continue;
             }
             if(OnSeg(p[],L[]) && OnSeg(p[],L[])){
                 print(L[]);continue;
             }
             if(OnSeg(p[],L[])){
                 m1 = get_pdis(p[],p[]);
                 m2 = d[] - m1;
                 solve(L[],m1,m2,p[],p[],p[],d[],d[],d[]);
                 continue;
             }
             if(OnSeg(p[],L[])){
                 m1 = get_pdis(p[],p[]);
                 m2 = d[] - m1;
                 solve(L[],m1,m2,p[],p[],p[],d[],d[],d[]);
                 continue;
             }
             if(OnSeg(p[],L[])){
                 m1 = get_pdis(p[],p[]);
                 m2 = d[] - m1;
                 solve(L[],m1,m2,p[],p[],p[],d[],d[],d[]);
                 continue;
             }
             printf("-1\n");
         }
         else printf("-1\n");
     }

     return ;
 }