『珂朵莉树 Old Driver Tree』

<更新提示>

<第一次更新>

---

<正文>

珂朵莉树

珂朵莉树其实不是树，只是一个借助平衡树实现的数据结构，主要是对于有区间赋值的数据结构题，可以用很暴力的代码很高效地完成任务，当然这是建立在数据随机的基础上的。

即使数据不是随机的，写一个珂朵莉树用来当做暴力也是很划算的。

珂朵莉树可以使用std::map来实现，并且代码量极小，不知道为什么大家都要写set。

维护方式

那么问题来了，如何使用\(map\)来实现珂朵莉树呢？众所周知，用\(set\)的实现方式都是维护一个连续的相同区间，\(map\)当然也是同理，我们仍然用\(map\)的第一维当数组下标，把相同一段元素的值存在段下标的最后一个位置，就比如这样：

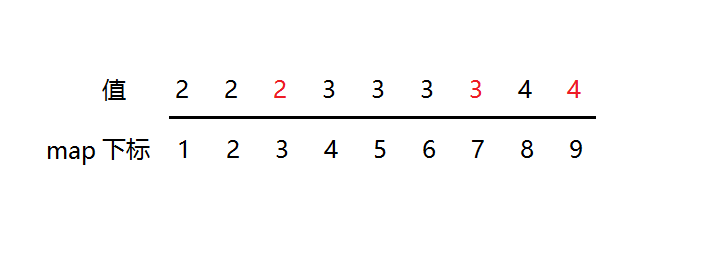
我们只在红色数字的下标位置申请\(map\)空间，存储数值。然后我们就可以非常方便的操作\(map\)了，看具体操作吧。

整体的定义和申明如下：

#define it map<int,int>::iterator
struct ChthollyTree
{
    map <int,int> s;
    inline int find(int p) { }
    inline void split(int p) { }
    inline pair<it,it> range(int l,int r) { }
};

find

我们需要实现珂朵莉树的\(find\)操作，就是在\(map\)中定位原数列一个位置的值。只需要使用\(map\)的\(lower\_bound\)操作找到段尾的位置即可，非常简单，没什么好说的。

inline int find(int p) { return s.lower_bound(p) -> second; }

spilt

珂朵莉树的\(split\)操作就是分裂一个区间，这方便我们维护原序列的区间操作。实现也非常简单，只需要直接调用\(find\)函数，再根据\(map\)维护段的定义，在最后一个位置申请空间，赋上值即可。

inline void split(int p)
{
    int pos = find(p);
    s[p] = pos;
}

值得注意的是，使用一个变量\(pos\)来记录\(find\)函数的结果是必须的，如果直接写\(s[p]=find(p)\)就会产生奇奇怪怪的错误。

为什么？首先，当我们写\(s[p]=find(p)\)时，\(find(p)\)函数还没有被调用，但是由于\(s[p]\)，\(map\)当中已经申请了一个二元组的位置\((p,0)\)，这样再调用\(find(p)\)，\(lower\_bound\)函数找到的值就不正确了。

难道等赋值号的结合律不是从右向左吗？原本是的，但是实测确实会有这样的问题，保险起见，我们使用\(STL\)容器的时候尽量不在一句话中同时调用和查找。

range

珂朵莉树的\(range\)操作就是提取出一整个完整的区间，并返回\(map\)的首尾迭代器，这样就可以执行具体的区间操作了。实现方法就是调用两次\(split\)函数。

inline pair<it,it> range(int l,int r)
{
    split(l-1) , split(r);
    return make_pair( s.find(l-1) , s.find(r) );
}

然后呢？ 没有然后了，我们已经实现珂朵莉树的全部功能了。

完整代码如下：

struct ChthollyTree
{
    map <int,int> s;
    inline int find(int p) { return s.lower_bound(p) -> second; }
    inline void split(int p)
    {
        int pos = find(p);
        s[p] = pos;
    }
    inline pair<it,it> range(int l,int r)
    {
        split(l-1) , split(r);
        return make_pair( s.find(l-1) , s.find(r) );
    }
};
ChthollyTree T;

那么如何实现具体的区间操作呢？别急，我们还需要看两种珂朵莉树的遍历方式。

完整遍历：区间修改

我们可以利用\(range\)函数提取区间，实现对一个区间在\(map\)中的完整遍历，从而实现区间修改操作：

map <int,int> :: iterator st,ed;
pair<it,it> border = T.range(l,r);
st = border.first , ed = border.second;
while ( st != ed ) ed->second += x , ed--;

如上就是一个区间加法的示例，我们先提取区间，然后用迭代器遍历\(map\)，再修改元素即可。

一般遍历：获取信息

当我们需要计算某一个区间的信息值时，不一定要提取区间，可以使用更好的方式遍历区间，直接计算即可：

ll sum = 0; int next;
for (int i=l;i<=r;i=next+1)
{
    it now = T.s.lower_bound(i);
    next = min( r , now->first );
    ll powsum = mul( next - i + 1 , quickpow( now->second , x , y ) , y );
    Add( sum , powsum , y );
}
printf("%lld\n",sum);

如上就是一个查询区间\(x\)次方和模\(y\)的示例，我们可以不断查询下一个段边界的迭代器，然后直接计算。

然后一个完整的珂朵莉树就得到实现了，剩下的操作也都可以通过上述的两种遍历实现，只要暴力就可以了。

Willem, Chtholly and Seniorious

Description

请你写一种奇怪的数据结构，支持：

• 1 l r x ：将[l,r]区间所有数加上x
• 2 l r x ：将[l,r]区间所有数改成x
• 3 l r x ：输出将[l,r]区间从小到大排序后的第x个数是的多少(即区间第x小，数字大小相同算多次，保证 1≤ x ≤ r-l+1)
• 4 l r x y ：输出[l,r]区间每个数字的x次方的和模y的值

Input Format

这道题目的输入格式比较特殊，需要选手通过seed自己生成输入数据。 输入一行四个整数n,m,seed,vmax（1≤ n,m≤10^5 ,0≤seed≤10^9+7 ,1≤vmax≤10^9 ） 其中n表示数列长度，m表示操作次数，后面两个用于生成输入数据。 数据生成的伪代码如下

def rnd():

    ret = seed
    seed = (seed * 7 + 13) mod 1000000007
    return ret

for i = 1 to n:

    a[i] = (rnd() mod vmax) + 1

for i = 1 to m:

    op = (rnd() mod 4) + 1
    l = (rnd() mod n) + 1
    r = (rnd() mod n) + 1

    if (l > r):
         swap(l, r)

    if (op == 3):
        x = (rnd() mod (r - l + 1)) + 1
    else:
        x = (rnd() mod vmax) + 1

    if (op == 4):
        y = (rnd() mod vmax) + 1

Output Format

对于每个操作3和4，输出一行仅一个数。

Sample Input

10 10 9 9

Sample Output

1 1 3 3

解析

就是一道模板题嘛，数据都是自己随机生成的。区间第\(x\)小的数字可以把数字段全部都取出来，然后排一下序二分查找。

\(Code:\)

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define it map<int,ll>::iterator
const int N = 1e5+20 , Mod = 1e9+7;
struct ChthollyTree
{
    map <int,ll> s;
    inline ll find(int p) { return s.lower_bound(p) -> second; }
    inline void split(int p)
    {
        ll pos = find(p);
        s[p] = pos;
    }
    inline pair<it,it> range(int l,int r)
    {
        split(l-1) , split(r);
        return make_pair( s.find(l-1) , s.find(r) );
    }
};
ChthollyTree T;
struct sec
{
    ll num; int cnt;
    sec (ll _num = 0,int _cnt = 0) { num = _num , cnt = _cnt; }
    friend bool operator < (sec p1,sec p2) { return p1.num < p2.num; }
};
int n,m,seed,vmax,a[N],sum[N],len;
sec p[N];
inline int random(void)
{
    int res = seed;
    seed = ( seed * 7LL + 13LL ) % Mod;
    return res;
}
inline ll add(ll a,ll b,ll mod) { return a + b >= mod ? a + b - mod : a + b; }
inline ll mul(ll a,ll b,ll mod) { return a * b % mod; }
inline void Add(ll &a,ll b,ll mod) { a = add( a , b , mod ); }
inline void Mul(ll &a,ll b,ll mod) { a = mul( a , b , mod ); }
inline ll quickpow(ll a,ll b,ll mod)
{
    ll res = 1; a %= mod;
    for ( ; b ; Mul(a,a,mod) , b>>=1 )
        if ( 1 & b ) Mul(res,a,mod);
    return res;
}
inline void input(void)
{
    scanf("%d%d%d%d",&n,&m,&seed,&vmax);
    for (int i=1;i<=n;i++)
    {
        a[i] = random() % vmax + 1;
        T.s[i] = a[i];
    }
    T.s[0] = T.s[n+1] = 0;
}
inline void solve(void)
{
    int op,l,r,x,y; int cnt=0;
    for (int i=1;i<=m;i++)
    {
        op = random() % 4 + 1;
        l = random() % n + 1 , r = random() % n + 1;
        if ( l > r ) swap( l , r );
        if ( op == 3 ) x = random() % (r-l+1) + 1;
        else x = random() % vmax + 1;
        if ( op == 4 ) y = random() % vmax + 1;
        map <int,ll> :: iterator st,ed;
        if ( op == 1 )
        {
            pair<it,it> border = T.range(l,r);
            st = border.first , ed = border.second;
            while ( st != ed ) ed->second += x , ed--;
        }
        if ( op == 2 )
        {
            pair<it,it> border = T.range(l,r);
            st = border.first , ed = border.second;
            while ( st != ed ) T.s.erase( ed-- );
            T.s[r] = x;
        }
        if ( op == 3 )
        {
            int next; len = 0;
            for (int i=l;i<=r;i=next+1)
            {
                it now = T.s.lower_bound(i);
                next = min( r , now->first );
                p[++len] = sec( now->second , next-i+1 );
            }
            sort( p+1 , p+len+1 );
            for (int i=1;i<=len;i++) sum[i] = sum[i-1] + p[i].cnt;
            int l = 1 , r = len;
            while ( l + 1 < r )
            {
                int mid = l + r >> 1;
                if ( x <= sum[mid] ) r = mid;
                else l = mid;
            }
            if ( x <= sum[r] && x > sum[l] ) printf("%lld\n",p[r].num);
            else printf("%lld\n",p[l].num);
        }
        if ( op == 4 )
        {
            ll sum = 0; int next;
            for (int i=l;i<=r;i=next+1)
            {
                it now = T.s.lower_bound(i);
                next = min( r , now->first );
                ll powsum = mul( next - i + 1 , quickpow( now->second , x , y ) , y );
                Add( sum , powsum , y );
            }
            printf("%lld\n",sum);
        }
    }
}
int main(void)
{
    input();
    solve();
    return 0;
}

---

<后记>