CodeForces 785 D Anton and School - 2 范德蒙恒等式

Anton and School - 2

题解：

枚举每个左括号作为必选的。

那么方案数就应该是下面的 1 ， 然后不断化简， 通过范德蒙恒等式 ， 可以将其化为一个组合数。

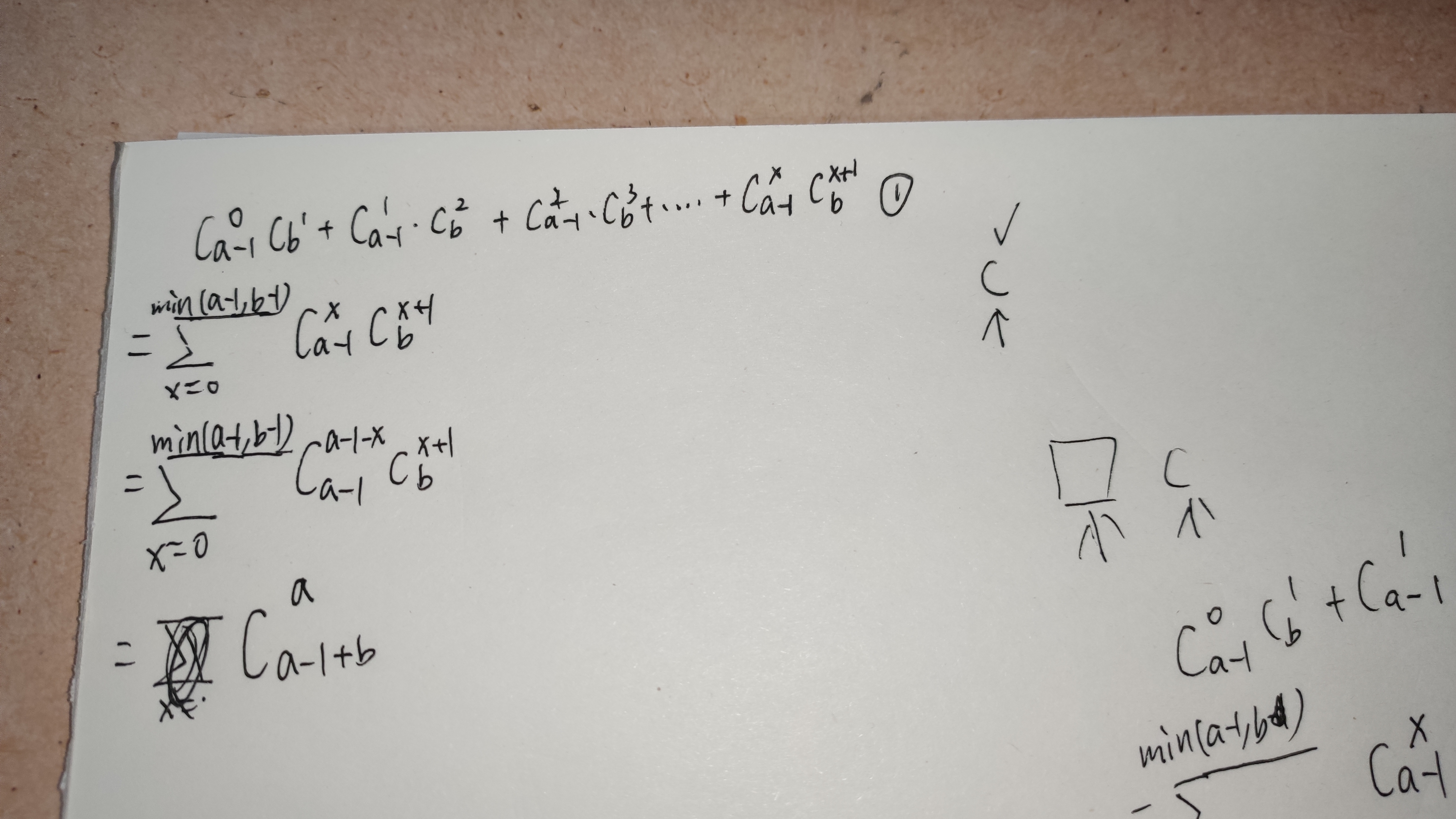
代码：

#include<bits/stdc++.h>
using namespace std;
#define Fopen freopen("_in.txt","r",stdin); freopen("_out.txt","w",stdout);
#define LL long long
#define ULL unsigned LL
#define fi first
#define se second
#define pb push_back
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define lch(x) tr[x].son[0]
#define rch(x) tr[x].son[1]
#define max3(a,b,c) max(a,max(b,c))
#define min3(a,b,c) min(a,min(b,c))
typedef pair<int,int> pll;
const int inf = 0x3f3f3f3f;
const int _inf = 0xc0c0c0c0;
const LL INF = 0x3f3f3f3f3f3f3f3f;
const LL _INF = 0xc0c0c0c0c0c0c0c0;
const LL mod =  (int)1e9+;
const int N = 2e5 + ;
int F[N], Finv[N], inv[N];/// F是阶层 Finv是逆元的阶层
void init(){
    inv[] = ;
    for(int i = ; i < N; i++)
        inv[i] = (mod - mod/i) * 1ll * inv[mod % i] % mod;
    F[] = Finv[] = ;
    for(int i = ; i < N; i++){
        F[i] = F[i-] * 1ll * i % mod;
        Finv[i] = Finv[i-] * 1ll * inv[i] % mod;
    }
}
int comb(int n, int m){ /// C(n,m)
    if(m <  || m > n) return ;
    return F[n] * 1ll * Finv[n-m] % mod * Finv[m] % mod;
}
char s[N];
int l[N], r[N];
int main(){
    scanf("%s", s+);
    int n = strlen(s+);
    for(int i = ; i <= n; ++i){
        if(s[i] == '(') l[i]++;
        l[i] += l[i-];
    }
    for(int i = n; i >= ; --i){
        if(s[i] == ')') r[i]++;
        r[i] += r[i+];
    }
    LL ans = ;
    init();
    for(int i = ; i <= n; ++i){
        if(s[i] == '('){
            ans = (ans + comb(l[i]-+r[i], l[i]))%mod;
        }
    }
    cout << ans << endl;
    return ;
}