st表、树状数组与线段树 笔记与思路整理

已更新（2/3）：st表、树状数组

st表、树状数组与线段树是三种比较高级的数据结构，大多数操作时间复杂度为O(log n)，用来处理一些RMQ问题或类似的数列区间处理问题。

---

一、ST表（Sparse Table）

st表预处理时间复杂度O(n log n)，查询O(1)，但不支持在线更改，否则要重新进行预处理。

使用一个二维数组：st[i][j]存储i为起点，长度为2^j的一段区间最值，即arr[i, i + 2^j - 1]。

具体步骤（以最小值为例）：

1. 将st[i][0]赋值为arr[i];
2. 利用动态规划思想，dp出st[i][j] = min(st[i][j - 1], st[i + 2^{j - 1}][j - 1])  (1 ≤ i ≤ n, 1 ≤ j ≤ log₂ n)；
3. 查询时，定义len为log₂(r - l + 1)，区间[l, r]的最小值为min(st[l][len],st[r - 2^len + 1][len])。

总时间复杂度为O(n log n + q)，q为请求数。

代码实现（两个st表分别求最大最小值）：

#include <bits/stdc++.h>
using namespace std;
int stmin[][], stmax[][];
int n, q, arr[], minans, maxans;
void init(){
    for(int j =  ; j <= n ; j++)stmax[j][]=stmin[j][]=arr[j];
    for(int i =  ; i <= log2(n) ; i++){
        for(int j =   ; j <= n ; j++){
            stmax[j][i] = stmax[j][i-];
            if(j + ( << (i-)) <= n ) stmax[j][i] = max(stmax[j][i], stmax[j+(<<(i-))][i-]);
            stmin[j][i] = stmin[j][i-];
            if(j + ( << (i-)) <= n ) stmin[j][i] = min(stmin[j][i], stmin[j+(<<(i-))][i-]);
        }
    }
}
void query(int l,int r){
    int len = log2(r - l + );
    minans = min(stmin[l][len],stmin[r - ( << len) + ][len]);
    maxans = max(stmax[l][len],stmax[r - ( << len) + ][len]);
}
int main(){
    scanf("%d %d", &n, &q);
    for(int i =  ; i <= n  ; i++)
        scanf("%d", &arr[i]);
    init();
    int l,r;
    for(int i =  ; i <= q ; i++ ){
        scanf("%d %d", &l, &r);
        query(l, r);
        printf("%d %d\n", minans, maxans);
    }
    return ;
}

2019.9.13 upd:

一点优化：每次计算2ⁿ或log₂n会比较慢，可以事先用两个数组初始化2ⁿ或log₂n的值。递推公式：

Bin[] = ;
for(int i=; i<; i++)
    Bin[i] = Bin[i-] * ;  //Bin[i]表示2的i次方
Log[] = -;
for(int i=; i<=; i++)
    Log[i] = Log[i/] + ;  //Log[i]表示以2为底i的对数

2019.9.20 upd:

预处理Bin数组（Bin[i] = 2ⁱ）与 1<<i 时间基本一致（但是log2(i)还是比较慢的，最好还是初始化Log数组）

---

二、树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)

树状数组是一种树状的结构（废话），但是只需要 O(n) 的空间复杂度。区间查询和单一修改复杂度都为 O(log n) ，经过差分修改后区间修改也可以达到 O(log n) ，但此时不能区间查询。通过维护多个数组可以达到 O(log n) 的区间修改与查询。

先来看一棵树（伪）。

一棵二叉树。

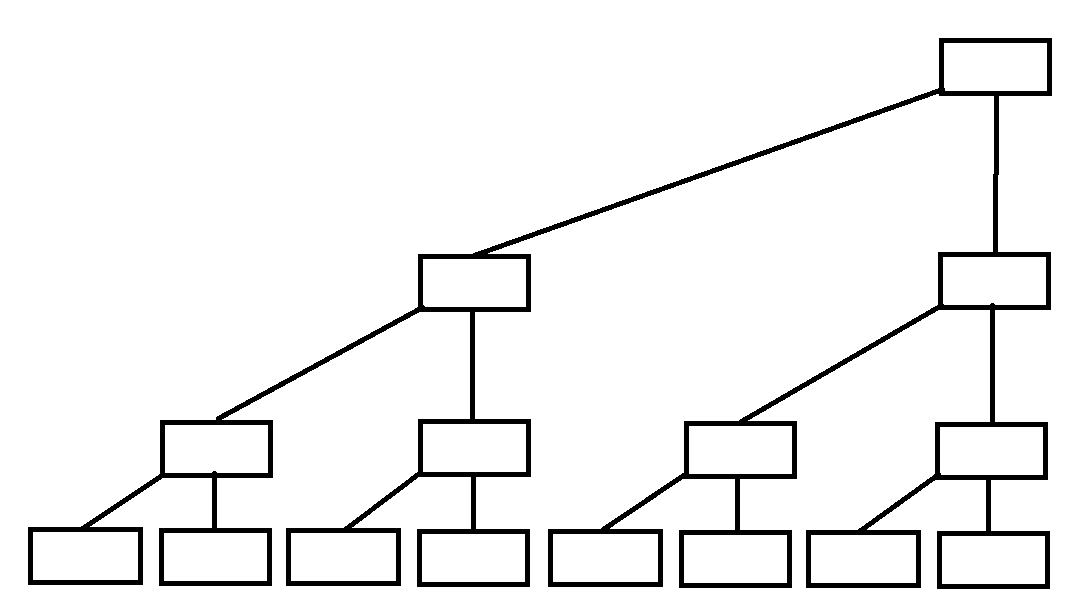
（图片均盗自网络QwQ）

如果要在一棵树上存储一个数组并且便于求和，我们可以想到让每个父节点存储其两个子节点的和。（就选择是你啦！线段树！）

为了达到 O(n) 的空间复杂度，删去一些节点（放弃线段树）后如下：

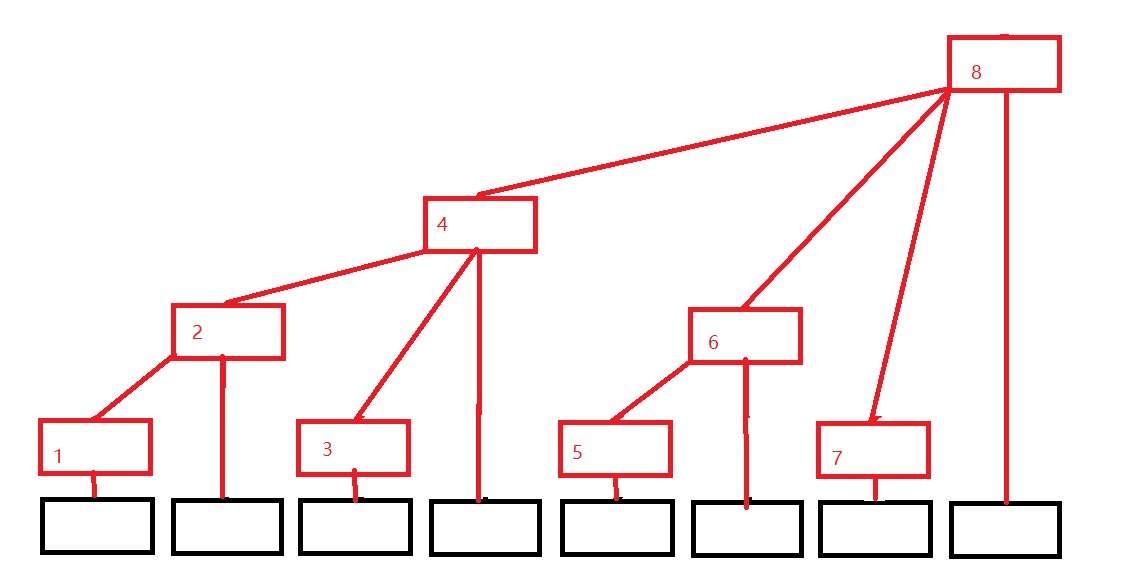
红色的为树状数组的节点，黑色为原始数组。每个树状数组的节点存储以其为根节点的子树上的所有值之和。

设 a[] 为原数组， t[] 为树状数组，则：

t[] = a[];
t[] = a[] + a[];
t[] = a[];
t[] = a[] + a[] + a[] + a[];
t[] = a[];
t[] = a[] + a[];
t[] = a[];
t[] = a[] + a[] + a[] + a[] + a[] + a[] + a[] + a[];

所以说，这棵树的（我自己没推出来的）规律是：

t[i] = a[i - 2^k + 1] + a[i - 2^k + 2] + ... + a[i]; //k为i的二进制中从最低位到高位连续零的长度

i的前缀和sum[i] = t[i] + t[i-2^k1] + t[(i - 2^k1) - 2^k2] + ...；

设lowbit(i) = 2^k , 则可以递推如下：

void add_node(int pos, int val){  //将节点pos增加val
    for(int i=pos; i<=n; i+=lowbit(i)){
        t[i] += val;
    }
}
int ask(int pos){  //求节点pos前缀和
    int ans = ;
    for(int i=pos; i>; i-=lowbit(i)){
        ans += t[i];
    }
    return ans;
}
int query_sum(int l, int r){  //利用前缀和求[l, r]总和
    return ask(r) - ask(l);
}

那么问题来了，怎么求这个 2^k 呢？

有一个巧妙的（我自己也没推出来的）算法是：

lowbit(x) = x & (-x);

抄一段证明如下：

这里利用的负数的存储特性，负数是以补码存储的，对于整数运算 x&(-x)有
       ● 当x为0时，即 0 & 0，结果为0；//因此实际运算的时候如果真的出现了lowbit(0)会卡死，要从1开始存储
       ●当x为奇数时，最后一个比特位为1，取反加1没有进位，故x和-x除最后一位外前面的位正好相反，按位与结果为0。结果为1。
       ●当x为偶数，且为2的m次方时，x的二进制表示中只有一位是1（从右往左的第m+1位），其右边有m位0，故x取反加1后，从右到左第有m个0，第m+1位及其左边全是1。这样，x& (-x) 得到的就是x。 
       ●当x为偶数，却不为2的m次方的形式时，可以写作x= y * (2^k)。其中，y的最低位为1。实际上就是把x用一个奇数左移k位来表示。这时，x的二进制表示最右边有k个0，从右往左第k+1位为1。当对x取反时，最右边的k位0变成1，第k+1位变为0；再加1，最右边的k位就又变成了0，第k+1位因为进位的关系变成了1。左边的位因为没有进位，正好和x原来对应的位上的值相反。二者按位与，得到：第k+1位上为1，左边右边都为0。结果为2^k。
        总结一下：x&(-x)，当x为0时结果为0；x为奇数时，结果为1；x为偶数时，结果为x中2的最大次方的因子。

1、区间查询与单点修改

具体讲解见上。

完整的树状数组单点修改和区间查询实现为：

（针对模板题：Luogu P3374）

#include <bits/stdc++.h>
using namespace std;
int a[], t[];
int n, m;
int lowbit(int x){
    return x & (-x);
}
void add_node(int pos, int val){
    for(int i=pos; i<=n; i+=lowbit(i)){
        t[i] += val;
    }
}
int query_node(int pos){
    int ans = ;
    for(int i=pos; i>; i-=lowbit(i)){
        ans += t[i];
    }
    return ans;
}
int query_range(int l, int r){
    return query_node(r) - query_node(l-);
}
int main(){
    cin >> n >> m;
    int opt, pos, l, r, num;
    for(int i=; i<=n; i++){
        scanf("%d", &a[i]);
        add_node(i, a[i]);
    }
    while(m--){
        scanf("%d", &opt);
        if(opt == ){
            scanf("%d%d", &pos, &num);
            add_node(pos, num);
        }
        if(opt == ){
            scanf("%d%d", &l, &r);
            printf("%d\n", query_range(l, r));
        }
    }
    return ;
}

2、单点查询与区间修改

那么，如何让线段树支持区间更改与单点查询呢？

设数组 b[i] = a[i] - a[i-1] ，用 t[] 表示 b[] 。

模拟算一次：

a[] = 1, 5, 4, 2, 3, 1, 2, 5

b[] = 1, 4, -1, -2, 1, -2, 1, 3

将区间[2, 5]加上1：

a[] = 1, 6, 5, 3, 4, 2, 2, 5

b[] = 1, 5, -1, -2, 1, -2, 0, 3

可以看到，只有 b[2] 和 b[6] 发生了变化。（即更改区间[l, r]时的节点l与节点r+1）因此，以 b[] 为原数组的 t[] 只需要执行两次 add_node() 即可。但是，在查询 a[i] 的时候就需要查询 b[1...i] 之和，在 log n 时间里只能查询单个节点的值。

完整的区间修改与单点查询代码实现：

（针对模板题：Luogu P3368）

#include <bits/stdc++.h>
using namespace std;
int a[], t[];
int n, m;
int lowbit(int x){
    return x & (-x);
}
void add_node(int pos, int val){
    for(int i=pos; i<=n; i+=lowbit(i)){
        t[i] += val;
    }
}
void add_range(int l, int r, int val){
    add_node(l, val);
    add_node(r+, -val);
}
int query_node(int pos){
    int ans = ;
    for(int i=pos; i>; i-=lowbit(i)){
        ans += t[i];
    }
    return ans;
}
int main(){
    cin >> n >> m;
    int opt, pos, l, r, num;
    for(int i=; i<=n; i++){
        scanf("%d", &a[i]);
        add_node(i, a[i] - a[i-]);
    }
    while(m--){
        scanf("%d", &opt);
        if(opt == ){
            scanf("%d%d%d", &l, &r, &num);
            add_range(l, r, num);
        }
        if(opt == ){
            scanf("%d", &pos);
            printf("%d\n", query_node(pos));
        }
    }
    return ;
}

3、区间查询与区间修改

简单谈一下区间查询与区间修改的操作：

（本段参考了xenny的博客）

∑ⁿ_{i = 1}a[i] = ∑ⁿ_{i = 1} ∑ⁱ_{j = 1}t[j];

则 a[1] + a[2] + ... + a[n]

= (t[1]) + (t[1] + t[2]) + ... + (t[1] + t[2] + ... + t[n])

= n * t[1] + (n-1) * t[2] + ... + t[n]

= n * (t[1] + t[2] + ... + t[n]) - (0 * t[1] + 1 * t[2] + ... + (n - 1) * t[n])

所以上式可以变为∑ⁿ_{i = 1}a[i] = n*∑ⁿ_{i = 1}t[i] -  ∑ⁿ_{i = 1}( t[i] * (i - 1) );

因此，维护两个树状数组，t1[i] = t[i]，t2[i] = t[i] * (i - 1);

具体修改及查询公式见完整代码实现：

（针对模板题：POJ 3468）

#include<iostream>
#include<cstdio>
using namespace std;
int n, m, maxn = ;
long long a[], t1[], t2[];
int lowbit(int x){
    return x & (-x);
}
void add_node(int pos, long long val){
    for(int i=pos; i<=n; i+=lowbit(i)){
        t1[i] += 1ll * val;
        t2[i] += 1ll * val * (pos-);
    }
}
void add_range(int l, int r, long long val){
    add_node(l, val);
    add_node(r+, -val);
}
long long query_node(int pos){
    long long ans = ;
    for(int i=pos; i>; i-=lowbit(i)){
        ans += 1ll * pos * t1[i] - t2[i];
    }
    return ans;
}
long long query_range(int l, int r){
    return query_node(r) - query_node(l-);
}
int main(){
    ios::sync_with_stdio(false);
    cin >> n >> m;
    char opt;
    int pos, l, r, num;
    for(int i=; i<=n; i++){
        cin >> a[i];
        add_node(i, a[i] - a[i-]);
    }

    while(m--){
        cin >> opt;
        if(opt == 'C'){
            cin >> l >> r >> num;
            add_range(l, r, num);
        }
        if(opt == 'Q'){
            cin >> l >> r;
            cout << query_range(l, r) << endl;
        }
    }
    return ;
}

---

三、线段树

每次基本操作（插入或删除）O(log n)，但是可以在不改变时间复杂度的情况下修改数据。

（正在更新）咕咕咕