数据结构 栈&队列
2-4
依次在初始为空的队列中插入元素a,b,c,d以后，紧接着做了两次删除操作，此时的队头元素是（ ）
删除，移动头指针；
增加，移动尾指针；
删除a，b ，队头c
2-3
在一个链队列中，front和rear分别为头指针和尾指针，则插入一个结点s的操作为（ ）
这道题目，我坚持自己的答案，就是这个答案！
2-1
若用大小为6的数组来实现循环队列，且当前front和rear的值分别为0和4。当从队列中删除两个元素，再加入两个元素后，front和rear的值分别为多少？
删除，front++
增加，rear++
是 2 和 6，循环队列 6%6=0
2 和 0
如果循环队列用大小为m的数组表示，队头位置为front、队列元素个数为size，那么队尾元素位置rear为
元素个数size = (rear-front+m)%m+1;
由此可得，rear = (size+front-1)%m;
编程题答案在我其他博客里，直接在侧栏搜索就行
代码：
设一个堆栈的入栈顺序是1、2、3、4、5。若第一个出栈的元素是4，则最后一个出栈的元素必定是：
设一个栈的输入序列是1、2、3、4、5，则下列序列中，是栈的合法输出序列的是？
解读下A：
1.压入 1 2 3
2.弹出 3 2 1
3.压入 4 5
4.弹出 5 4
出栈顺序就是 3 2 1 5 4，成立，别的也可以用相同的方式进行分析；
将5个字母ooops按此顺序入栈，则有多少种不同的出栈顺序可以仍然得到ooops？
可以看出，最后两个ps都是压入后就弹出的，所以就是研究 ooo的弹出组合；
ooo
队列&栈函数题（只补充之前博客里没有的）
- 堆栈操作合法性（ 分）
假设以S和X分别表示入栈和出栈操作。如果根据一个仅由S和X构成的序列，对一个空堆栈进行操作，相应操作均可行（如没有出现删除时栈空）且最后状态也是栈空，则称该序列是合法的堆栈操作序列。请编写程序，输入S和X序列，判断该序列是否合法。
输入格式:
输入第一行给出两个正整数N和M，其中N是待测序列的个数，M（≤）是堆栈的最大容量。随后N行，每行中给出一个仅由S和X构成的序列。序列保证不为空，且长度不超过100。
输出格式:
对每个序列，在一行中输出YES如果该序列是合法的堆栈操作序列，或NO如果不是。
输入样例：
SSSXXSXXSX
SSSXXSXXS
SSSSSSSSSSXSSXXXXXXXXXXX
SSSXXSXXX
输出样例：
YES
NO
NO
NO
----------------------------------------------------------------------
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <iostream>
#define EXP_STACK 50
#define ERROR -1
#define OK 1
using namespace std;
typedef int Elemtype;
typedef int Status;
;
int STACK_SIZE;
typedef struct
{
Elemtype *base;
Elemtype *top;
int sta_len;
int ElemNumber;
}Stack;
Status InitStack(Stack &Sta)
{
Sta.base = (Elemtype *)malloc(STACK_SIZE*sizeof(Elemtype));
;
Sta.top = Sta.base;
Sta.sta_len = STACK_SIZE;
Sta.ElemNumber = ;
}
Status GetTop(Stack sta,Elemtype &e)
{
if(sta.top==sta.base) return ERROR;
e = *(sta.top-);
return OK;
}
Status Push(Stack &S,Elemtype e)
{
if(S.top-S.base>=S.sta_len)
{
S.base = (Elemtype *)realloc(S.base,(EXP_STACK+S.sta_len)*sizeof(Elemtype));
S.sta_len+=EXP_STACK;
}
*S.top++ = e;
S.ElemNumber+=;
return OK;
}
Status Pop(Stack &S)
{
if(S.top==S.base) return ERROR;
--S.top;
S.ElemNumber--;
return OK;
}
int main()
{
int cases;
int Len;
scanf("%d%d",&cases,&Len);
STACK_SIZE = Len;
while(cases--)
{
];
scanf("%s",opr);
int len = strlen(opr);
Stack Sta;
InitStack(Sta);
//cout<<Sta.sta_len<<" "<<Sta.ElemNumber<<endl;
bool Fits = true;
;i<len;i++)
{
if(opr[i]=='S')
{
if(Sta.ElemNumber==Len)
{
Fits = false;
break;
}
Push(Sta,);
}
else if(opr[i]=='X')
{
int Ans = Pop(Sta);
)
{
Fits = false;
break;
}
}
}
if(Sta.ElemNumber) Fits = false;
if(Fits)
cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
}
}
堆栈操作合法性
- 符号配对（ 分）
请编写程序检查C语言源程序中下列符号是否配对：/*与*/、(与)、[与]、{与}。
输入格式:
输入为一个C语言源程序。当读到某一行中只有一个句点.和一个回车的时候，标志着输入结束。程序中需要检查配对的符号不超过100个。
输出格式:
首先，如果所有符号配对正确，则在第一行中输出YES，否则输出NO。然后在第二行中指出第一个不配对的符号：如果缺少左符号，则输出?-右符号；如果缺少右符号，则输出左符号-?。
输入样例1：
void test()
{
];
; i<; i++) /*/
A[i] = i;
}
.
输出样例1：
NO
/*-?
输入样例2：
void test()
{
int i, A[10];
for (i=0; i<10; i++) /**/
A[i] = i;
}]
.
输出样例2：
NO
?-]
输入样例3：
void test()
{
int i
];
; i<; i++) /**/
A[i] = 0.1*i;
}
.
输出样例3：
YES
--------------------------------------------------------------------
#include<cstdio>
#include<iostream>
#include<cmath>
#include<malloc.h>
#include<stdlib.h>
#include<string.h>
#include<cstring>
#define STACK_INIT_SIZE 10000
#define STACKINCREMENT 10
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
using namespace std;
typedef char SElemType,Status;
typedef struct
{
SElemType *base;
SElemType *top;
int stacksize;
} Stack;
Status InitStack(Stack &S)
{
S.base=(SElemType *)malloc(sizeof(SElemType)*STACK_INIT_SIZE);
if(!S.base)
exit(OVERFLOW);
S.top=S.base;
S.stacksize=STACK_INIT_SIZE;
return OK;
}
Status Push(Stack &S,SElemType e)
{
if(S.top-S.base>=S.stacksize)
{
S.base=(SElemType*)malloc(sizeof(SElemType)*(S.stacksize+STACKINCREMENT));
if(!S.base)
exit(OVERFLOW);
S.top=S.base+S.stacksize;
S.stacksize+=STACKINCREMENT;
}
*S.top++=e;
return OK;
}
Status Pop(Stack &S)
{
if(S.top==S.base)
return ERROR;
S.top--;
return OK;
}
Status GetTop(Stack &S,SElemType &e)
{
if(S.base==S.top)
return ERROR;
e=*(S.top-);
return OK;
}
+;
char s[maxn];
bool Find(Stack &S,char ch)
{
char tmp[maxn];
memset(tmp,'\n',sizeof(tmp));
;
while(S.top!=S.base)
{
SElemType e2;
GetTop(S,e2);
if(e2==ch)
{
Pop(S);
; i>=; i--)
Push(S,tmp[i]);
return true;
}
else
{
tmp[num++]=e2;
}
Pop(S);
}
; i>=; i--)
Push(S,tmp[i]);
return false;
}
void judge(char ch)
{
if(ch=='(')
printf("(-?\n");
else if(ch=='[')
printf("[-?\n");
else if(ch=='{')
printf("{-?\n");
else if(ch=='<')
printf("/*-?\n");
}
int main()
{
Stack Sta;
InitStack(Sta);
;
while(gets(s))
{
]=='.') break;
int len=strlen(s);
;i<strlen(s);i++)
{
if(s[i]=='('||s[i]=='['||s[i]=='{')
Push(Sta,s[i]);
]==<len)
{
++i;
Push(Sta,'<');
}
else if(s[i]==')')
{
if(Sta.top!=Sta.base)
{
SElemType e;
GetTop(Sta,e);
if(e=='(')
Pop(Sta);
else if(flag)
{
printf("NO\n");
flag=;
judge(e);
}
}
else if(flag)
{
flag=;
printf("NO\n");
printf("?-)\n");
}
}
else if(s[i]==']')
{
if(Sta.top!=Sta.base)
{
SElemType e;
GetTop(Sta,e);
if(e=='[')
Pop(Sta);
else if(flag)
{
printf("NO\n");
flag=;
judge(e);
}
}
else if(flag)
{
flag=;
printf("NO\n");
printf("?-]\n");
}
}
else if(s[i]=='}')
{
if(Sta.top!=Sta.base)
{
SElemType e;
GetTop(Sta,e);
if(e=='{')
Pop(Sta);
else if(flag)
{
printf("NO\n");
flag=;
judge(e);
}
}
else if(flag)
{
flag=;
printf("NO\n");
printf("?-}\n");
}
}
]==<len)
{
++i;
if(Sta.top!=Sta.base)
{
SElemType e;
GetTop(Sta,e);
if(e=='<')
Pop(Sta);
else if(flag)
{
printf("NO\n");
flag=;
judge(e);
}
}
else if(flag)
{
flag=;
printf("NO\n");
printf("?-*/\n");
}
}
}
}
if(flag)
{
if(Sta.base==Sta.top)
printf("YES\n");
else
{
SElemType e;
GetTop(Sta,e);
printf("NO\n");
judge(e);
}
}
}
符号配对
简单的递归策略非常好理解：
只用一个题举例子：
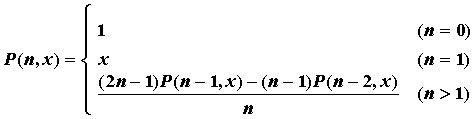
double P( int n, double x )
{
if(n==0) return 1; // 条件一
else if(n==1) return x;//条件二
else if(n>1)
{
return ((2*n-1)*P(n-1,x)-(n-1)*P(n-2,x))/n;//条件三
}
}
这就是根据条件和参数还原一下；
Made by Kindear
数据结构 栈&队列的更多相关文章
- 数据结构之队列and栈总结分析
一.前言: 数据结构中队列和栈也是常见的两个数据结构,队列和栈在实际使用场景上也是相辅相成的,下面简单总结一下,如有不对之处,多多指点交流,谢谢. 二.队列简介 队列顾名思义就是排队的意思,根据我们的 ...
- 数据结构和算法(Golang实现)(14)常见数据结构-栈和队列
栈和队列 一.栈 Stack 和队列 Queue 我们日常生活中,都需要将物品排列,或者安排事情的先后顺序.更通俗地讲,我们买东西时,人太多的情况下,我们要排队,排队也有先后顺序,有些人早了点来,排完 ...
- java 集合 Connection 栈 队列 及一些常用
集合家族图 ---|Collection: 单列集合 ---|List: 有存储顺序 , 可重复 ---|ArrayList: 数组实现 , 查找快 , 增删慢 ---|LinkedList: 链表实 ...
- Java 容器之 Connection栈队列及一些常用
集合家族图 ---|Collection: 单列集合 ---|List: 有存储顺序 , 可重复 ---|ArrayList: 数组实现 , 查找快 , 增删慢 ---|LinkedList: 链表实 ...
- C++ 泛型 编写的 数据结构 栈
平时编程里经常需要用到数据结构,比如 栈和队列 等, 为了避免每次用到都需要重新编写的麻烦现将 C++ 编写的 数据结构 栈 记录下来,以备后用. 将 数据结构 栈 用头文件的形式 ...
- java面向对象的栈 队列 优先级队列的比较
栈 队列 有序队列数据结构的生命周期比那些数据库类型的结构(比如链表,树)要短得多.在程序操作执行期间他们才被创建,通常用他们去执行某项特殊的任务:当完成任务之后,他们就会被销毁.这三个数据结构还有一 ...
- JavaScript数据结构——栈的实现与应用
在计算机编程中,栈是一种很常见的数据结构,它遵从后进先出(LIFO——Last In First Out)原则,新添加或待删除的元素保存在栈的同一端,称作栈顶,另一端称作栈底.在栈中,新元素总是靠近栈 ...
- javascript数据结构之队列
首先什么是队列? 排队买东西就是生活中队列的实际例子,在队伍中大家必须按照顺序来,不能插队,新来的人只能排在队伍的最后面.新加入的人相当于队列的后端加入的元素,队伍最前面买完东西的人离开队伍相当于是队 ...
- 栈 & 队列
栈 先进者后出,后进者先出,LIFO,典型的"栈"结构 从栈的操作特性上来看,栈是一种"操作受限"的线性表,只允许在一段插入和删除数据. 在功能上来说,数组和链 ...
随机推荐
- 深度学习之 GAN 进行 mnist 图片的生成
深度学习之 GAN 进行 mnist 图片的生成 mport numpy as np import os import codecs import torch from PIL import Imag ...
- 《深入实践Spring Boot》阅读笔记之二：分布式应用开发
上篇文章总结了<深入实践Spring Boot>的第一部分,这篇文章介绍第二部分:分布式应用开发,以及怎么构建一个高性能的服务平台. 主要从以下几个方面总结: Spring Boot SS ...
- JAVAFX-5 开发应用
fx 属性与布局 属性与布局是一个具备gui开发能力的开发者,快速进入开发必备的知识储备,下面简单说一说常用的属性,与布局 颜色 颜色 在 javafx.scene.paint.Color 类中提供了 ...
- mysql中出现Unknown column 'qwe' in 'field list'的错误
下面是我建表的代码 输入数据的代码 可以看到出现了类似Unknown column 'qwe' in 'field list'的错误 当时看了好久改了又改都没有找到错误,直道我在一次打C语言代码的过程 ...
- type="file"实现兼容IE8本地选择图片预览
一.HTML代码 <%@ Page Language="C#" AutoEventWireup="true" CodeBehind="Uploa ...
- [转]scrapy中的logging
logging模块是Python提供的自己的程序日志记录模块. 在大型软件使用过程中,出现的错误有时候很难进行重现,因此需要通过分析日志来确认错误位置,这也是写程序时要使用日志的最重要的原因. scr ...
- jacascript DOM节点——节点关系与操作
前言:这是笔者学习之后自己的理解与整理.如果有错误或者疑问的地方,请大家指正,我会持续更新! 节点关系 DOM可以将任何HTML描绘成一个由多层节点构成的结构.每个节点都拥有各自的特点.数据和方法,也 ...
- jmeter出现卡死或内存溢出的解决方案
故事背景:在初次使用jmeter的时候,把线程设置较大值的时候,jmeter工具很容易就卡死了,导致每次做压测的时候都无法顺利完成,非常的闹心,通过各种方法寻找解决方案,终于找到了一个比较靠谱的方法, ...
- 自定义Loader
自定义Loader涉及到的接口: public delegate byte[] CustomLoader(ref string filePath); public void LuaEnv.AddLoa ...
- java中包的定义
对包中的java程序进行编译(cmd) 编译:javac -d . Test.java 执行:java com.java.demo.Test package com.java public class ...