机器学习中 K近邻法(knn)与k-means的区别

简介

K近邻法（knn）是一种基本的分类与回归方法。k-means是一种简单而有效的聚类方法。虽然两者用途不同、解决的问题不同，但是在算法上有很多相似性，于是将二者放在一起，这样能够更好地对比二者的异同。

算法描述

knn

算法思路：
如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。

k近邻模型的三个基本要素：

1. k值的选择：k值的选择会对结果产生重大影响。较小的k值可以减少近似误差，但是会增加估计误差；较大的k值可以减小估计误差，但是会增加近似误差。一般而言，通常采用交叉验证法来选取最优的k值。
2. 距离度量：距离反映了特征空间中两个实例的相似程度。可以采用欧氏距离、曼哈顿距离等。
3. 分类决策规则：往往采用多数表决。

k-means

算法步骤：
1. 从n个数据中随机选择 k 个对象作为初始聚类中心；
2. 根据每个聚类对象的均值（中心对象），计算每个数据点与这些中心对象的距离；并根据最小距离准则，重新对数据进行划分；
3. 重新计算每个有变化的聚类簇的均值，选择与均值距离最小的数据作为中心对象；
4. 循环步骤2和3，直到每个聚类簇不再发生变化为止。

k-means方法的基本要素：

1. k值的选择：也就是类别的确定，与K近邻中k值的确定方法类似。
2. 距离度量：可以采用欧氏距离、曼哈顿距离等。

应用实例

问题描述

已知若干人的性别、身高和体重，给定身高和体重判断性别。考虑使用k近邻算法实现性别的分类，使用k-means实现性别的聚类。

数据

数据集合：https://github.com/shuaijiang/FemaleMaleDatabase

该数据集包含了训练数据集和测试数据集，考虑在该数据集上利用k近邻算法和k-means方法分别实现性别的分类和聚类。

将训练数据展示到图中，可以更加直观地观察到数据样本之间的联系和差异，以及不同性别之间的差异。

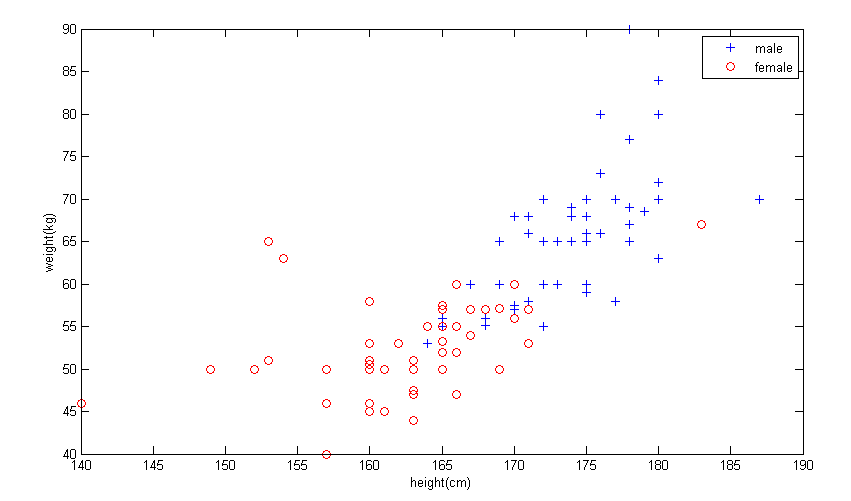数据展示

KNN的分类结果

KNN算法中的基本设置

• k=5
• 距离度量：欧氏距离
• 分类决策规则：多数投票
• 测试集：https://github.com/shuaijiang/FemaleMaleDatabase/blob/master/test0.txt

利用KNN算法，在测试集上的结果如下混淆矩阵表所示。从表中可以看出，测试集中的男性全部分类正确，测试集中的女性有一个被错误分类，其他都分类正确。

混淆矩阵	Test:male	Test:female
Result:male	20	1
Result:female	0	14

（表注：Test:male、Test:female分别表示测试集中的男性和女性，Result:male和Result:female分别表示结果中的男性和女性。表格中第一个元素：即Test:male列、Result：male行，表示测试集中为男性、并且结果中也为男性的数目。表格中其他元素所代表的含义以此类推）
由上表可以计算分类的正确率：(20+14)/(20+14+1) = 97.14%

K-means的聚类结果

K-means算法的基本设置

• k=2
• 距离度量：欧氏距离
• 最大聚类次数：200
• 类别决策规则：根据每个聚类簇中的多数决定类别
• 测试集：https://github.com/shuaijiang/FemaleMaleDatabase/blob/master/test0.txt

混淆矩阵	Test:male	Test:female
Result:male	20	1
Result:female	0	14

（表注：该表与上表内容一致）

由于选择初始中心点是随机的，所以每次的聚类结果都不相同，最好的情况下能够完全聚类正确，最差的情况下两个聚类簇没有分开，根据多数投票决定类别时，被标记为同一个类别。

KNN VS K-means

二者的相同点:
- k的选择类似
- 思路类似：根据最近的样本来判断某个样本的属性

二者的不同点：

• 应用场景不同：前者是分类或者回归问题，后者是聚类问题;
• 算法复杂度： 前者O（n^2）,后者O（kmn）;（k是聚类类别数，m是聚类次数）
• 稳定性：前者稳定，后者不稳定。

总结

本文概括地描述了K近邻算法和K-means算法，具体比较了二者的算法步骤。在此基础上，通过将两种方法应用到实际问题中，更深入地比较二者的异同，以及各自的优劣。本文作者还分别实现了K近邻算法和K-means算法，并且应用到了具体问题上，最后得到了结果。
以上内容难免有所纰漏和错误，欢迎指正。