清北学堂4.28Day1(重大更新详见贪心例一)
枚举
用题目中给定的检验条件判定哪些是无用的,哪些是有用 的。能使命题成立的即为其解 。
例一
一棵苹果树上有n个苹果,每个苹果长在高度为Ai的地方。
小明的身高为x
他想知道他最多能摘到多少苹果
数据范围: 1 ≤ n, Ai, x ≤ 100
题解
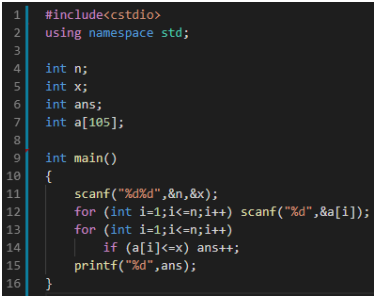
问题相当于询问有多少i满足Ai <= x,考虑用for循环枚举每一个苹果是否能被摘到即可。
例二
筛素数
判断一个数X是否是素数
1 ≤ X ≤ 1e9
考虑定义,若X为合数,则必然有:
∃1 < i < X, i|X
我们考虑直接枚举每个i,看他是否为X的因子。时间复杂度是O(N),不符合要求
事实上我们发现,假设X是一个合数,那么必然有:
X = a * b,必然有:
min(a, b) <= √X
因此我们枚举的范围可以从X变为√X
时间复杂度O(√N)

例三
求[l, r]这段区间中有多少素数
1 ≤ l ≤ r ≤ 1e6
Emmmm我是真的不想再写一遍筛法了咕咕咕咕
例四
求[l, r]这段区间中有多少素数
1 ≤ l ≤ r ≤ 1e6
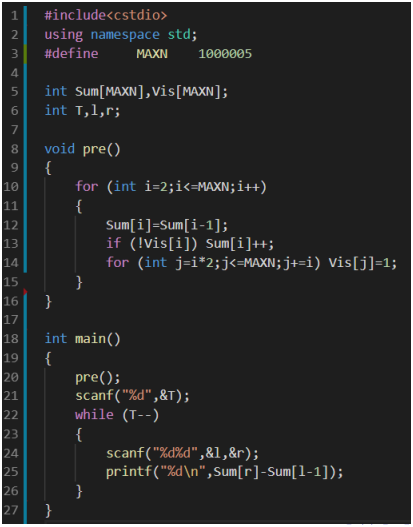
这里直接先预处理,然后问的时候输出就可以了
例五
已知n个整数x1, x2, .., xn,以及一个整数k,k < n。从n个数字
中任选k 个整数相加,可分别得到一系列的和。
例如当n = 4, k = 3,四个整数分别为3,7,12,19时,可得全部的组合与他们的和为:
3 + 7 + 12 = 22
3 + 7 + 19 = 29
7 + 12 + 19 = 38
3 + 12 + 19 = 34
现在,要求计算出和为素数的组合共有多少种。例如上例,只有一种组合的和为素数:3 + 7 + 19 = 29
1 ≤ n ≤ 20, k < n
1 ≤ x1, x2, .., xn ≤ 5e6
题解
首先我们来考虑如何枚举这样的组合。
我们用ai来表示第i个数是否被选,ai = 1表示这个数被选择了,ai = 0表示这个数未被选择
枚举过程相当于枚举了一组二进制状态
比如对于五个数1,2,3,4,5
01010表示我们选择了2,4,未选择1,3,5,枚举过程相当于枚举了一组二进制状态
在不考虑k的限制的情况下,我们枚举所有组合就相当于
枚举00..00(n个0) → 11..11(n个1)
对于任意一种中间状态,0的个数+1的个数为n
我们假设这是一个长为n的二进制数,我们将它转换成十进
制。
事实上就是枚举了一个数,范围是[0, 2n)
判断位置i是否为1使用位运算来完成
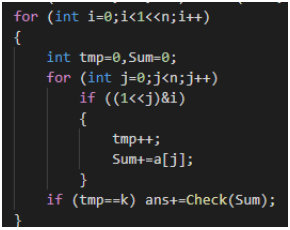
Check部分即为判断是否为素数。考虑到最大Sum不超过20 * 500w,预处理出10000以内的素
数可以加速
例六
求[l,r]中有多少数既是回文数又是素数
1 ≤ l ≤ r ≤ 1e7
策略一
枚举每个数,判断他是不是回文数,判断他是不是素数
时间复杂度O(N√N + NlogN
策略二
预处理出区间所有素数,枚举素数判定是否是回文数
时间复杂度O(NlogN)
策略三
枚举区间内所有回文数,判断是否是素数
枚举回文数即枚举一个数的前一半,再手动扩展成完整的数,另外,偶数位数的回文数都必然是11的倍数,不需要枚举。
时间复杂度O(√N * √N) =
O(N)
先枚举回文数的话能够快一点;
枚举算法有以下特点
优点
简单明了,分析直观
能够帮助我们更好地理解问题
运用良好的枚举技巧可以使问题变得更简单
缺点
时空间效率低
往往没有利用题目中的特殊性质
产生了大量冗余状态
搜索算法(本质是枚举)
一般用来做一些普通的枚举不方便表达状态的情况
给出一个N*N的迷宫,求从起点出发,不经过障碍物到达终
点的最短距离

解决这种问题一般有两种方式
- 深度优先搜索
- 广度优先搜索
深度优先搜索(DFS)的前置知识
栈:后进先出的数据结构
支持的操作:
加入一个数
删除最晚加入的数
查询最晚加入的数
实现:一个数组+一个用于指向栈顶位置的变量
举个例子:
斐波那契数列

现在来看看具体的操作过程
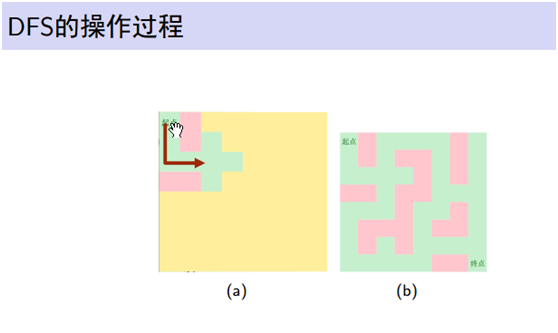
枚举四个方向,如果可以走那么我们把那个位置压进栈中,产生分叉的时候就随意选择一个方向,直到不能继续走为止
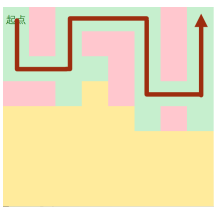
因为我们有一个栈,那么我们把这个点从栈里扔出去,选择另一个方向,然后就一直走啊走啊走,这样就得到了一条路径
但是我们会发现,按照这种走法,我们能得到多种解
比如以下情况

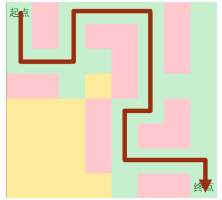
所以DFS的缺点和优点就有了
优点:占用空间小(只需要记录从起点到当前点的路径)
代码短
缺点:获得的不一定是最优解
在图上路径非常多的时候,复杂度可能会达到指数级别
PS:这是不会出现死循环的,因为同一个路径我们只会走一次
扩充一个例题:

这样的话写深搜试一试
设一个vis[]数组表示每一个点是否被访问过
如果是多组数据,可以尝试用一个过程去实现多组数据(这是一个很好的技巧)
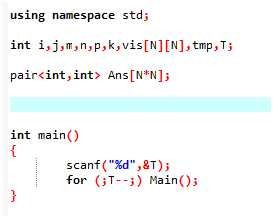
注意这里的Main是大写

如果既没有墙壁也没有出界,那么这个位置是可以走下去的,写一个check函数有助于我们对于一个点快速判断
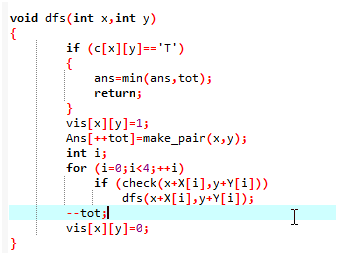
这里这个pair<int,int>是一个二元组,我们把这个二元组存到队列里头,实际用法和struct是一样的,在我之前的实现里头也用过二维数组的方式
在dfs完了之后一定要注意把数据还原
给变量命名的时候要注意一定不能重名
虽然fz尴尬了好多次,但是它至少教给我们了一个调试代码的好思想,就是在某些你认为的断点上直接输出数组,这样的话就能直接看出来数组是不是对的了
下面来看广度优先搜索
前置知识
队列:先进先出的数据结构
支持的操作:
加入一个数
删除最早加入的数
查询最早加入的数
实现:一个数组+头下标+尾下标
看一下操作过程吧

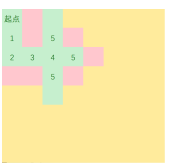
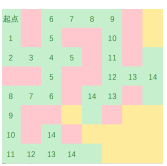
广搜实现的基本思想,先搞一个队列,然后弄一个xy的数组,来存上下左右的方式
优点是得到的解一定是最优解,而且时间复杂度一定是小于等于整张地图的,因为每一个点至多走一遍,而且BFS是完全可以替代DFS的,但是DFS的优点是空间占用少
缺点:BFS虽然简单好想,但是需要维护一个“当前箭头的集合”代码非常长,而且占用了非常多的空间
DFS和BFS的区别
DFS:能走就走,走不了才回头
BFS:我全都要(真捞啊)

图可以分为有向图和无向图,存图的方式有两种,第一个是邻接矩阵,另一种是链式前向星(当然你可以用vector)
存图方式
1.画图
2.邻接矩阵存储,用A[x][y] = 0/1表示.优点是便于加删,但是需要O(N2)的空间.
3.直接用vector存下所有的边(邻接表法).优点是空间和访问比较快,缺点是删除比较麻烦
Map[x][y]
表示从x到y是否有边(若是有向图尤其要注意顺序)
Vector是一个任意长度的数组

你可以弄一个任意类型的vector

Push_back表示加入一个值
Pop_back表示删掉一个值
但是如果i比数组长度大的时候,程序就会re
Vector慢的原因是每当一个长度被填满了之后,在增加一个新元素的时候,会重新申请一个两倍的内存空间,然后再把现有的值赋值进去
图的连通块
在本课中我们基本只考虑无向图.
若a沿着边走可以到b,则称a与b在同一个连通块中,称a与b连通.
显然a与b连通,b与c连通,则a与c肯定连通一张图可以被分成若干个两两连通的块.
给出一张n个点m条边的图,分别求出每个连通块.
n, m ≤ 100000.
用bfs还是dfs?(肯定是后者啦)
每次任选一个没有被访问过的点,然后从这个点开始bfs,找到所有和它连通的点.
时间复杂度O(N + M)(用什么方式可以让每条边被遍历常数遍?)
跑图的连通块和跑矩阵的连通块没啥区别,(可以看看细胞数量这道题)无非就是用vector存图而已
Vector最好的应用就是树

遍历一个树
给出一棵n个点的树,将它转化为有根树的形式(假定以1为根)
N ≤ 100000
用bfs还是dfs?
理论上来说bfs和dfs都可以,但一般我们用dfs构造.
复杂度O(N).
例题
例一
要求输出1 ∼ n构成的全排列
用一个Vis数组记录每个数字是否被用过
DFS的经典应用
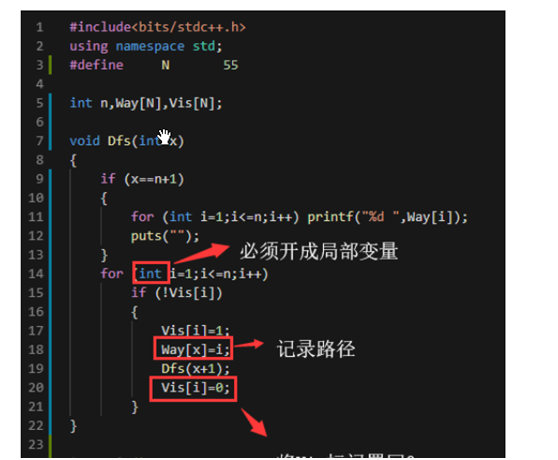
例二
八数码游戏是一种非常无聊的游戏。给定一个3*3的格子,在其中8个格子中放置整数1 ∼8,剩下一个格子空着(用0表示)。每次操作时,你可以选择将某个与空格相邻的数字移动到空格上。给定一个初始局面,求最少需要多少次操作才能将局面变成
1 2 3
4 5 6
7 8 0
题解
状态?0 ∼8 的一个排列
转移?一步能够到达的其他排列
BFS or DFS? BFS
如果有多组数据呢?
考虑倒着进行游戏过程。
所有状态都是由最终状态转移得到的
因此我们以最终态为起点做一遍BFS即可预处理出所有状态的答案
求出每个点最少需要多少步就可以了
例三
给出一个大小为N*M的迷宫,问从起点到终点最少经过多少障碍物
1 ≤ n, m ≤ 1000
肯定是用BFS
在搜到每一个点的时候,如果有一个点是有障碍的,那么所有能够达到这个点的路径ans++
这里我们维护两个队列,分别表示当前答案和答案+1的点
每次先走同层的点即可
例四
跳房子
跳房子是大家小时候的体育游戏之一,游戏的规则简单易懂、具有可变性。我们在地面上画出一个个房子,然后扔石子,根据石子的落地位置确定跳到哪个房子。我们将房子抽象为x轴上的连续的正整数坐标点,第i个房子的坐标为i,并假设房子个数无限。
我们的游戏规则如下:1. 石子落到房子内,记为H,我们可以跳到当前坐标的3倍坐标位置。2. 石子落到房子外,记为O,我们需跳回当前坐标折半并向下取整的坐标位置。
例如,初始在第1个房子,要想到达第6个房子,既可以HHHOO,也可以HHOHO。请你编一个程序,给出从第n个房子到第m个房子所需要的最少跳跃次数k和石子的扔法。若最少跳跃次数下存在多种扔法,则选取字典序最小的扔法。
1 ≤ N, M ≤ 1000,数据保证在25步之内有解。
这个题使用BFS可能会有些问题,因为无法预知最远能跳到多远。
但是注意到数据在25步之内一定会出解,我们不妨考虑暴力dfs,在dfs的时候遵循先H后O的规律.
时间复杂度O(pow(2 , 25)).
例五
推箱子
推箱子是一个很经典的游戏.今天我们来玩一个简单版本.在一个M * N的房间里有一个箱子和一个搬运工,搬运工的工作就是把箱子推到指定的位置,注意,搬运工只能推箱子而不能拉箱子,因此如果箱子被推到一个角上那么箱子就不能再被移动了,如果箱子被推到一面墙上,那么箱子只能沿着墙移动.现在给定房间的结构,箱子的位置,搬运工的位置和箱子要被推去的位置,请你计算出搬运工至少要推动箱子多少格.
N, M ≤ 7
题解
因为要求求出至少推动箱子多少格,所以我们得用BFS,暴力记录人的位置和箱子的位置作为一个4维的状态,然后进行bfs.
为什么这里是四维呢?,主要的原因就是要考虑到人的位置能不能推箱子,这一点在写BFS得时候没啥问题,但是在判断的时候就非常变态了,你必须得写非常非常多的判断函数才能保证状态是合法的
时间复杂度O(N * M * N * M).
之后来一个比较刺激的
迷宫入口
爱好探险的你,找到一座装满了宝藏的迷宫的入口,你看到入口的大门上有一个边长为s的正方形的大锁,旁边散落着n块正方形的金属小片,你意识到锁的钥匙,即是用这n小块,拼成大门上的正方形,你想知道是否能拼成这把钥匙打开迷宫的大门。
n ≤ 16, 1 ≤ ci ≤ 10.
这里考虑直接用深搜的方式去搜,首先我们不是枚举某一个正方形放在那里,而是枚举某个点放哪个正方形
搜的时候,我们选下表面最低的那个点,而且选择最靠左的
Vector表示最底层
我们还要判断会不会超过边界,而且放的正方形的下表面必须是没有方块的,否则就得用一个更小的正方形来放
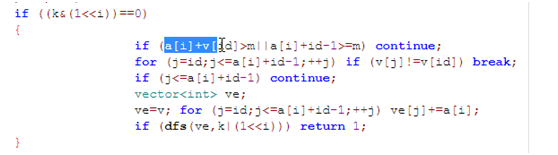
但是这个代码TLE了,所以我们得剪一下枝
每次我们不要去重复的选择一个长度相同的正方形,这样就能通过本题了.
时间复杂度O(玄学)(剪枝真的很炫学啊).
最后看一个非常bt的题

每次操作可以将任一个固体块向上、向下、向左或向右平移一格,但是在平移的过程中不能使得任何两个固体块有重合的部分。问是否能够通过上述的操作使得三个固体块完全分离。完全分离指对于任何两个不同的固体块,完全覆盖它们的最小的长方形没有重合的部分。如果能做到,输出所需要的最小的步数,如果做不到,输出-1。所有方块的坐标范围都在0到9之间。
是一个相当复杂的BFS最短路题,难点在于如何构建合适的状态.
这里我们把它降维打击一下(只记录四个坐标)我们可以设计初始状态(x1, y1, x2, y2, x3, y3),分别记录三个块的左上角位置,注意到每一维的坐标可能在(-20, 20)之间,所以状态会很多.
我们来尝试将一些状态隐藏起来,不妨强制x1, y1是当前坐标轴的(0,0),然后这样我们只需要记录另外两个点的位置就行了。因为事实上只有相对位置是有用的,可以少计一个。注意到每一维的范围仍然是(-20, 20),所以状态数被我们缩减到了40^4就可以接受了
来看最初的斐波那契数列
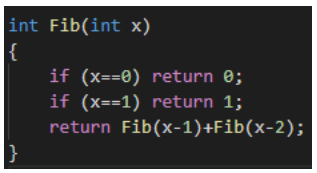
时间复杂度?
O(2N)
发现复杂度的主要来源是有很多次重复计算考虑用f[i]记录Fib数列的第i项当搜索到这一项时不再进行递归,而是直接返回答案这就是
传说中的记忆化搜索
3.贪心
每一步都取当前的最优解的思想一般来说符合直观思路,需要严格的证明,OI中使用多个错误的贪心策略进行加成有时会有良好的效果(是这样的,因为自己写的贪心算法的正确性是需要证明的,多个贪心凑一块,有的时候玄学一点也能过大部分点了)
例一(P1208 [USACO1.3]混合牛奶 Mixing Milk)
怎么说呢,usaco总是很喜欢奶牛啊QWQ这个题也是在_GC大佬的帮助下才发现有误的,就一块讲一讲吧
很水的一道题,一个sort就行了
具体怎么弄呢?
首先我们把每个农民排序,优先让价格低的人在前,价格相同时奶牛多的人在前,这个用cmp实现就可以
然后排完序直接跑一遍统计ans,输出就行了QWQ神仙竟然还能做错这种题目
#include <cstdio>
#include <algorithm>
#include <iostream>
using namespace std;
struct QAQ
{
int milk, price;
} people[];
bool cmp(QAQ a, QAQ b)
{ if (a.price != b.price)
return a.price < b.price;
else
return a.milk > b.milk;
}
int main()
{
int n, m, ans=;
scanf("%d%d", &n, &m);
for (int i = ; i <= n; ++i)
scanf("%d%d", &people[i].price, &people[i].milk);
sort(people + , people + m + , cmp);
int i=;
while(n)
{
if(people[i].milk)
{
people[i].milk--;
n--;
ans+=people[i].price;
}//如果这个农民的奶牛用完了就换下一个
else i++;
}
printf("%d",ans);
return ;
}
例二
给定n个物品,第i个物品有大小li,要求将这些物品装进容积为L的箱子里,每个箱子至多放两个物品,求最少所需箱子数。
1 ≤ n ≤ 1e5
题解
将物品从大到小排序
考虑当前的最大物品,假设能与最小值凑成一对,就凑成一对,否则必然不存在一个物品能与他凑成一对,因此单列用双指针维护这个过程即可
例三
有n个物品,每个物品有属性Ai和Bi。你需要将他们排成一行 ,如果物品i被放在第j个位置,那么会产生代价Ai · (j - 1) + Bi · (n - j),现在要求总代价的最小值1 ≤ n ≤ 1e5
展开式子
得到ans = ΣAi · j - Ai + Bi · n - Bi · j
发现 Bi · n - Ai 是常数,会变化的只有Ai · j - Bi · j
所以我们按照ai-bi排序
例四
给定n个水龙头,第i个水龙头有最大出水量Ai,且给定一个温度值ti。定义水龙头i一次出水得到的温度为Σ(Ai *ti)/Σ(Bi) ,给定一次出水得到的温度T,求最大总出水量。如果得不到该温度,输出0
1 ≤ n ≤ 2 * 1e5, 0 ≤ Ai, ti ≤ 1e6
先把ti减去T,然后按照t排序。把数组分成两块,一半小于等于0,一半大于0。用贪心的思想,可以发现有一半必须全选,另一半选最靠近T的那些

证明:
假设负数集里面还有一些没选,正数集里还有数剩余,那么我们就可以把他们凑出一个0出来,直到某一边用完为止.证毕.
所以就可以直接贪心了

例五


贪心策略3是正确的
例六
有两个工作所用时间t1t2,截止时间d1d2,那么延迟的时间就是max(t1+s-d1,)有n个闹钟,第i(1
≤ i ≤ n)个闹钟将在第ai(1
≤ ai ≤ 1e6)分钟鸣响,鸣响时间为一分钟。当在连续的m分钟内,有至少k 个闹钟鸣响,则会被叫醒。现要求关闭一些闹钟,使得在任意连续的m分钟内,鸣响的闹钟数量恒小于k。

二分的思想
给定一个单调的函数/数组,给定一个值,求这个值是否存在,或者找到这个值应当存在的位置
一个例子,在一个单调递增的数列当中,求是否有8
来看 1
2 3 4 5 7 8 这个序列,每一次都找中间的那个数,然后和目标数进行比较,来进行选择,到底是去掉左端点还是右端点,我们会发现,每一次数据范围都是/2的,所以算法的最差时间复杂度就是O(log
N)
当这一次二分和上一次是一个点的时候,那么他们相差一定不超过1了,就达到精度要求了

我们要找一个最大的X合法,当大于x的答案都是非法的,那么我们就对所有的答案区间进行二分,直到找到最大的合法X
举个例子
例一
一条河上有n个石子排成一条直线,第i个石子距离河岸xi。一只年长的青蛙想要从岸边(x=0处)到达第n个石子上(其实是对岸)。这只青蛙实在是太年长了,所以最多只能跳m次,而且他希望他这些次跳跃中距离最远的那次距离尽可能的短。请你帮他求出这个最远距离最短能是多少。
1 ≤ m ≤ n
≤ 1e5
题解
最小化:最大的跳跃距离
二分答案:设答案为mid,则问题变为:
n个石子,只能跳m次,每次跳远距离不能超过mid,问是否可行。或者n个石子,每次最远距离不超过mid,问最少跳多少次(然后和m比较即可)。
这里我们的判断方式是二分
对于每一个二分出来的答案我们进行判断
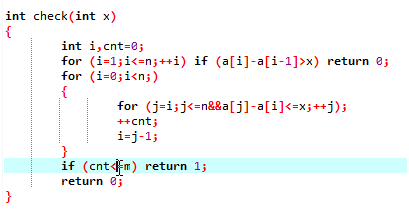
先看会不会有跳不到的石头,然后看跳跃次数有没有超过m,然后二分即可
例二
给定n个物品,每个物品有属性Ai和Bi。要求在其中选择k个物品,使得选择的物品的sum(A)/sum(B)尽可能大。
这里其实首先想到的就是贪心,其次才是二分。
但是贪心一定对么?
贪心:选Ai/Bi最高的k个物品?
反例:
3 2
1000 10
1000 100
1 1
除了最优的物品一定会选之外 可以考虑选择Bi非常小的物品, 减小对性价比的影响。此时物品3比物品2 更优。
所以我们来二分
二分答案
假设sum(Ai)/sum(Bi) >=
mid
则:sum(Ai) - mid * sum(Bi) >=
0
即:sum(Ai-mid*Bi) >=
0
将Ai-mid*Bi作为第i个物品的权值,问题变为能否选k个物品使得权值和大于0.此时贪心选择权值最大的k个物品即可。
二分复杂度O(logN)* 排序O(NlogN)
= O(Nlog 2N)
例三
给出一个长度为n的序列A1, A2, .., An,给出值r,k,定义一个sum[i]表示区间[i-r,i+r]中Aj的和,可以对这个序列进行不超过k次操作,每次操作选择一个Ai使其变为Ai +
1求min(sum[i]) 的最大值
如给出长度为5的序列5
4 3 4 9,给定r=0,k=6,那么序列可以变为6 6 5 5 9,得出最优解min(sum[i])=5
1 ≤ r ≤ n
≤ 500000, k
≤ 10 18
二分是对一个单调的函数进行的操作
那么我们有没有办法对一个单峰的函数进行操作呢?
求一个单峰函数的极值点
三分
参考二分的做法,我们把区间划成三份。
然后比较中间两个点的大小
来进行一下讨论
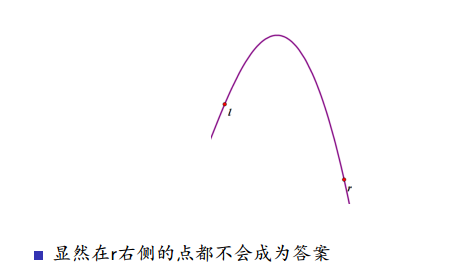


发现共性:l,r中值较小的那一段一定会被舍去,
严格的实现每次都能缩小问题的 1/3,事实上我们取两次mid会好写很多,只是常数问题
例一
初始有一个为空的集合,要求支持两种操作
1.不断向集合中插入一个数,且这个数比集合中所有数都大
2.在集合中找一个子集,使得找到的子集S中的最大值减去子集S中元素的平均值的差最大,并输出这个差
操作数≤ 500000
首先我们肯定要选对最大的数字,然后问题就在于我们到底选前k小的数,那么到底k是多少呢?
这里考虑三分,是这样的,当数量已开始比较小的时候,平均值会变小,但是随着数字变多,有的数字比平均值大了,那么他就会把平均值拉高,所以大概的图像就是Y=-X^2的这种,跑一下三分就OK了
代码实现如下


三分还有一个技巧,就是说当三分的距离很短的时候,我们三分反而会慢,所以直接打个暴力就行了
现在到了喜闻乐见的分治环节了(大雾)
分治的思想
将一个问题划分成若干个(一般都是分成俩)子问题
分别解决每个子问题后(也可能是前,还可能一前一后之类的)
将各个子问题组合起来得到原问题的答案。
快速幂
如何快速计算X k?

我们将k进行二进制拆分。
比如我们需要计算X 11即我们需要计算X 20+21+23,因此我们只需要计算logk 次即可
归并排序
基本思想:先将整个数组分成两个部分,分别将两个部分排好序,然后将两个排好序的数组O(n)合并成一个数组。
我们将问题分为两个阶段:分、治
分
对于每个长度> 1的区间,拆成两个[l, mid]区间
和[mid +
1, r]区间
直接递归下去

这样的话就可以一直递归直到只剩下一个数的时候,就分完了
治
我们认为在处理区间[l,r]时,已经有[l,mid]和[mid+1,r]内分别有序,这一次的操作就是合并两个有序序列,成为一个新的长有序序列。
用两个指针分别指向左右分别走到哪了即可
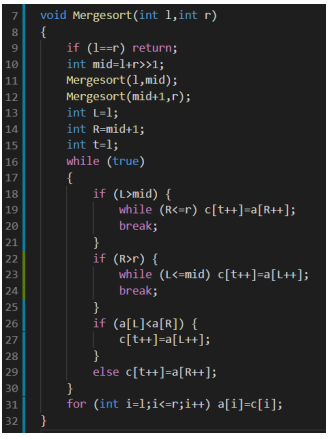
这里其实就是用两个指针分别从要合并的两个数组的头元素指起,如果元素被合并,那么就指针++,直到两个数组的指针都指完为止,就是这一块
算法的时间复杂度就是O(nlogN)
来看例题
逆序对
给定一个1 ∼n的排列,求逆序对数量。
1 ≤ n ≤ 105
逆序对:对于1 ≤ x
< y ≤ n, 若A[x] >
A[y],则称(x,y)为一
个逆序对。
题解
首先显然我们枚举x,y可以做到O(N2)
分治:
假设当前问题 Work(l,r) 是求l到r区间内的逆序对数量。
讨论所有(x,y)可能在的位置:
l ≤ x <
y ≤ mid :子问题Work(l,mid)
x ≤ mid <
y : ???
mid + 1 ≤ x
< y ≤ r
:子问题Work(mid+1,r)
对于每个mid右边的数,我们要找到mid左边有多少比它大的数。
1) 对左侧排序,右侧在左侧上二分即可。 总时间复杂度O(nlog2n)
2) 归并排序:
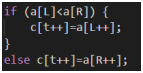
对于数组A和数组B的归并过程,每当我们将B中的元素取出时:说明A中最小的元素比该元素大:说明A中所有元素比该元素大:说明 答案+=A.size()
归并过程时间复杂度O(n),总时间复杂度O(nlogn)。
例二
有一个序列,初始时只有一个数n
对于序列中每一个> 1的数,拆分成三个数n/2,n%2,n/2并替换原数。
直到序列中没有> 1的数为止,查询最终序列中[l, r]中有多少1
0 ≤ n < 250, 0 ≤ r
- l ≤ 105
以15为例
F(15)=2f(7)+1;
这样我们递归出来就行了
例三

有一个例子

平面最近点对
给定二维平面上的N个点,求任意两点间的最近距离(欧几里得距离)。
1 ≤ n ≤ 105
题解
不妨按照x坐标排序。对于区间[l,r],我们将其分成mid左右
两个部分。
两个点都在左侧:子问题Work(l,mid)
两个点都在右侧:子问题Work(mid+1,r)
两个点一个在左侧,一个在右侧:
重点考虑第三种情况
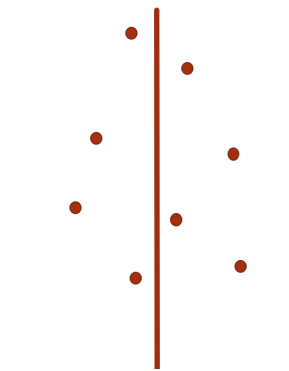
不妨假设左右两个子问题的答案为ans。则我们只需要考虑分界线两边距离不超过ans以内的点即可。
不妨假设左右两个子问题的答案为ans。则我们只需要考虑分界线两边距离不超过ans以内的点即可
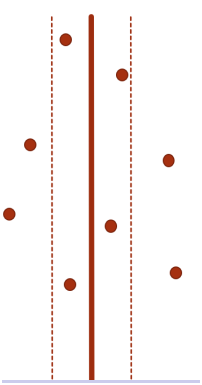

每个小正方形内点数不可能超过一个(因为任意两点距离不低于ans)。故总点数不超过6个。除去该点自身,该点至多需要和其他6个点求距离。故该部分复杂度不超过O(n)。实现时可以直接对所有点按照y坐标排序,O(n
log2 n),或者使用归并排序的技巧,直接O(n
log n)即可。

清北学堂4.28Day1(重大更新详见贪心例一)的更多相关文章
- 7月清北学堂培训 Day 3
今天是丁明朔老师的讲授~ 数据结构 绪论 下面是天天见的: 栈,队列: 堆: 并查集: 树状数组: 线段树: 平衡树: 下面是不常见的: 主席树: 树链剖分: 树套树: 下面是清北学堂课程表里的: S ...
- 清北学堂2017NOIP冬令营入学测试P4745 B’s problem(b)
清北学堂2017NOIP冬令营入学测试 P4745 B's problem(b) 时间: 1000ms / 空间: 655360KiB / Java类名: Main 背景 冬令营入学测试 描述 题目描 ...
- 清北学堂2017NOIP冬令营入学测试 P4744 A’s problem(a)
清北学堂2017NOIP冬令营入学测试 P4744 A's problem(a) 时间: 1000ms / 空间: 655360KiB / Java类名: Main 背景 冬令营入学测试题,每三天结算 ...
- 济南清北学堂游记 Day 1.
快住手!这根本不是暴力! 刷了一整天的题就是了..上午三道题的画风还算挺正常,估计是第一天,给点水题做做算了.. rqy大佬AK了上午的比赛! 当时我t2暴力写挂,还以为需要用啥奇怪的算法,后来发现, ...
- 清明培训 清北学堂 DAY1
今天是李昊老师的讲授~~ 总结了一下今天的内容: 1.高精度算法 (1) 高精度加法 思路:模拟竖式运算 注意:进位 优化:压位 程序代码: #include<iostream>#in ...
- <知识整理>2019清北学堂提高储备D2
简单数据结构: 一.二叉搜索树 1.前置技能: n/1+n/2+……+n/n=O(n log n) (本天复杂度常涉及) 2.入门题引入: N<=100000. 这里多了一个删除的操作,因此要 ...
- 清北学堂2017NOIP冬令营入学测试
P4744 A's problem(a) 时间: 1000ms / 空间: 655360KiB / Java类名: Main 背景 冬令营入学测试题,每三天结算一次成绩.参与享优惠 描述 这是一道有背 ...
- <知识整理>2019清北学堂提高储备D3
全天动态规划入门到入坑... 一.总概: 动态规划是指解最优化问题的一类算法,考察方式灵活,也常是NOIP难题级别.先明确动态规划里的一些概念: 状态:可看做用动态规划求解问题时操作的对象. 边界条件 ...
- 清北学堂2017NOIP冬令营入学测试P4749 F’s problem(f)
时间: 1000ms / 空间: 655360KiB / Java类名: Main 背景 冬令营入学测试 描述 这个故事是关于小F的,它有一个怎么样的故事呢. 小F是一个田径爱好者,这天它们城市里正在 ...
随机推荐
- C#的Lock
有时候在编写线程并发的时候需要考虑异步和同步的问题.有些资源只能是一个线程访问,其他的线程在这个线程没有释放资源前不能访问.类似于操作系统中临界资源的访问.C#Lock包裹的代码块具有原子操作的特性( ...
- java的设计模式 - Builder模式
Builder 模式的目的? 构造对象的方式过于复杂,不如将之抽离出来.比如,构造器参数过多 这样说也有点抽象,举个例子吧. 举个例子 比如 非常热门的消息队列RabbitMQ 的 AMQP.Basi ...
- .net开源工作流ccflow从表数据数据源导入设置
第1节. 关键字 驰骋工作流引擎 流程快速开发平台 workflow ccflow jflow .net开源工作流 第2节. 从表数据导入设置 1.1.1: 概要说明 在从表的使用中我一般都会用到从 ...
- Android常用的四种布局(或者说是五种)
一.FrameLayout(帧布局): 显示特点:所有的子控件默认显示在FrameLayout的左上角,会重叠在一起显示. 常用属性: layout_gravity(设置给子控件,调整控件在容器内的重 ...
- Android:随机生成算数四则运算简单demo(随机生成2~4组数字,进行加减乘除运算)
首先创建一个新的Android工程,下面是页面布局: Java代码: 我们先来分析一下如何完成的步骤: 1.首先,先完成生成随机数.(包括随机生成几组数字,范围为多少的数字,四则运算符号等): 2.要 ...
- 我带着小程序和Springboot后端终于战胜了WebSocket!!!胜利( •̀ ω •́ )y
WebSocket项目笔记 1. What is WebSocket? (以下内容来源于百度百科) WebSocket是一种在单个TCP连接上进行全双工通信的协议 WebSocket使得客户端和服务器 ...
- c语言static关键字的理解
static 一.概述 在c语言中static恰当的使用能让程序更加完美,细节上的严谨,代码会更好,也更利于程序的维护与扩展. 而static使用灵活,且又有两种完全无关的用法,所以整理总结一下. 二 ...
- IBM developer:Kafka ACLs
Overview In Apache Kafka, the security feature is supported from version 0.9. When Kerberos is enabl ...
- pyhton从开始到光棍的day11
纪念我这个开始学python的光棍天,光棍天依旧是函数,这次的函数有个小高级,比昨天的low函数稍微高级点,就是在使用函数中是可以赋值的,比如索引一个值什么的.函数还可以当做参数进行传递,把这个函数名 ...
- random使用方法
random.random() 没有参数,选择0到1之间的随机浮点数 random.uniform(a, b) 生成指定范围内的随机浮点数如果a.b哪个大那个小都没关系,生成的都是在小的与大的之间的随 ...
