luoguP3598 Koishi Loves Number Theory

题目

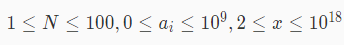
题解

等比数列，最后统一除以(x-1)（这里数据都存在逆元。。。。）

（不存在逆元可以考虑表示成：x*p^y的pair形式，最后上下把p的次数相减（类似扩展Lucas）

具体操作：(a,b)*(c,d)=(a*c,b+d)

然后检查(a,b)：如果a%mod==0,(a,b)->(a/mod,b+1)，否则(a,b)->(a%mod,b)

显然这样取模，mod的次数不会减少。

）

求：lcm(x^(ai+1)-1)

令f(a)=x^(a+1)-1

一看，根本无法直接做

上一个这样lcm的是：51nod斐波那契最小公倍数，gcd(f[a],f[b])=f[gcd(a,b)]

利用gcd和lcm的容斥关系！

这个是否也可以？

不妨考虑gcd(f(a),f(b))

发现，利用辗转相减可以证明：gcd(f(a),f(b))=gcd(f(b),f(a-b))=f(gcd(a,b))

但是要考虑所有的集合。。。

结论：gcd不会太多

开个map，暴力遍历枚举

每个map[i].fi存gcd，map[i].se存这个gcd贡献的指数次数（上-下）

拼凑ai新加的gcd把原来贡献取反加入即可。

最后++map[a[i]]

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
#define pb push_back
#define solid const auto &
#define enter cout<<endl
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
template<class T>il void output(T x){if(x/)output(x/);putchar(x%+'');}
template<class T>il void ot(T x){if(x<) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}
 
namespace Miracle{
const int N=;
const int mod=1e9+;
ll x,n;
ll a[N];
int qm(int x,int y){
    int ret=;
    while(y){
        if(y&) ret=(ll)ret*x%mod;
        x=(ll)x*x%mod;
        y>>=;
    }
    return ret;
}
unordered_map<int,int>mp,t;
int gcd(int a,int b){
    return b?gcd(b,a%b):a;
}
int main(){
    rd(x);rd(n);
    x%=mod;
    for(reg i=;i<=n;++i) rd(a[i]),++a[i];
    for(reg i=;i<=n;++i){
        t=mp;
        for(solid j:mp){
            int g=gcd(j.fi,a[i]);
            t[g]+=-j.se;
        }
        t[a[i]]++;
        mp.swap(t);
    }
    ll ans=;
    for(solid j:mp){
        if(j.se>=) ans=ans*qm((qm(x,j.fi)+mod-)%mod,j.se)%mod;
        else ans=ans*qm(qm((qm(x,j.fi)+mod-)%mod,-j.se),mod-)%mod;
    }
    ans=(ll)ans*qm((x+mod-)%mod,mod-)%mod;
    ot(ans);
    return ;
}
 
}
signed main(){
    Miracle::main();
    return ;
}
 
/*
   Author: *Miracle*
*/

min-max容斥吼啊

结论吼啊

暴力吼啊