NDT(Normal Distribution Transform) 算法(与ICP对比)和一些常见配准算法
原文地址:http://ghx0x0.github.io/2014/12/30/NDT-match/
By GH
发表于 12月 30 2014
目前三维配准中用的较多的是ICP迭代算法,需要提供一个较好的初值,同时由于算法本身缺陷,最终迭代结果可能会陷入局部最优。本文介绍的是另一种比较好的配准算法,NDT配准。这个配准算法耗时稳定,跟初值相关不大,初值误差大时,也能很好的纠正过来。
绪论:
- 采样:
- 3d点云数据在离相机近处点云密度大,远处密度小,所以在下采样时采用统一的采样方法还是会保留密度不均匀;
一种方法是将空间划分格子,在每个格子内的点云随机取点,点数足够了即可。 - 短波将会产生更高的分辨率和较少的镜面反射。采用多个深度相机会产生串扰的问题,尤其是镜面反射很厉害的时候。
- 3d点云数据在离相机近处点云密度大,远处密度小,所以在下采样时采用统一的采样方法还是会保留密度不均匀;
可以采集图像深度的相机:
- 雷达radio
- 激光雷达lidar
- 三角测量法
- TOF飞行时间法
- 相位差法
- 声呐
- 双目视觉
- 双目视觉是一个被动的三角测量;
缺点:
A.双目视觉只有能被检测出来的特征点才能检测出深度,在低对比度的环境中,只有很少的特征点能够检测出;
B.双目视觉的另一个缺点是岁两个相机之间的距离增大,深度精度减少,盲区增大,主要面向几米远的长距离测量。
C.对于没有纹理的表面检测不出来。
- 双目视觉是一个被动的三角测量;
- 投影光三角测量
- TOF深度相机
- 实际上是采用相位偏移法测量;
TOF深度相机相比lidar的TOF是 采集速度快,硬件便宜
缺点是噪点很明显,并且需要标定,并且受外界光和本身主动光的影响。 而且曝光时间不容易确定
- 实际上是采用相位偏移法测量;
视图匹配(配准):
- ICP
缺点:A.要剔除不合适的点对(点对距离过大、包含边界点的点对)
B.基于点对的配准,并没有包含局部形状的信息
C.每次迭代都要搜索最近点,计算代价高昂
存在多种优化了的变体算法,如八叉树等
- IDC
ICP的一种改进,采用极坐标代替笛卡尔坐标进行最近点搜索匹配
- PIC
考虑了点云的噪音和初始位置的不确定性
- Point-based probabilistic registration
需要首先建立深度图的三角面片
- NDT——正态分布变换:
计算正态分布是一个一次性的工作(初始化),不需要消耗大量代价计算最近邻搜索匹配点
概率密度函数在两幅图像采集之间的时间可以离线计算出来
- Gaussian fields
和NDT正态分布变换类似,利用高斯混合模型考察点和点的距离和点周围表面的相似性
- Quadratic patches
- Likelihood-field matching——随机场匹配
- CRF匹配
缺点: 运行速度慢,在3d中实时性能不好,误差大。
- Branch-and-bound registration
- Registration using local geometric features
NDT算法:
- 将空间(reference scan)划分成各个格子cell
- 将点云投票到各个格子
计算格子的正态分布PDF参数

将第二幅scan的每个点按转移矩阵T的变换
第二幅scan的点落于reference的哪个 格子,计算响应的概率分布函数
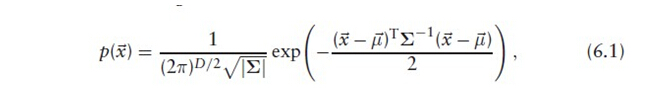
求所有点的最优值,目标函数为
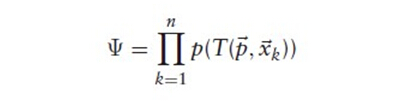
PDF可以当做表面的近似表达,协方差矩阵的特征向量和特征值可以表达表面信息(朝向、平整度)
格子内少于3个点,经常会协方差矩阵不存在逆矩阵,所以只计算点数大于5的cell,涉及到下采样方法。
- NDT的优化:
格子参数最重要,太大导致精度不高,太小导致内存过高,并且只有两幅图像相差不大的情况才能匹配
- 固定尺寸
- 八叉树建立,格子有大有小
- 迭代,每次使用更精细的格子
- K聚类,有多少个类就有多少个cell,格子大小不一
- Linked-cell
- 三线插值 平滑相邻的格子cell导致的不连续,提高精度
缺点:插值导致时间是普通的4倍
优点:可以提高鲁棒性
ICP算法:
- 给定参考点集P和数据点集Q(在给定初始估计RT时)
- 对Q中的每一个点寻找P中的对应最近点,构成匹配点对
- 对匹配点对求欧氏距离和作为误差目标函数error
- 利用SVD分解求出R和T,使得error最小
- 将Q按照R和T旋转变化,并以此为基准回到1 重新寻找对应点对
NDT 耗时稳定,跟初值相关不大,初值误差大时,也能很好的纠正过来;
ICP耗时多,容易陷入局部最优;
可以根据格子cell的PDF的协方差矩阵计算特征向量特征值,每个格子有球形状、平面、线型三种类型,根据朝向作以统计,得到局部或者一幅图像的特征直方图
文章来自于Martin Magnusson的The Three-Dimensional Normal-Distributions Transform— an Efficient Representation for Registration,Surface Analysis, and Loop Detection。 作者详细介绍了NDT在各个条件下的配准效果及与其他配准方法的详细实验对比,并利用NDT算法配准矿洞内三维场景,同时完成SLAM任务。
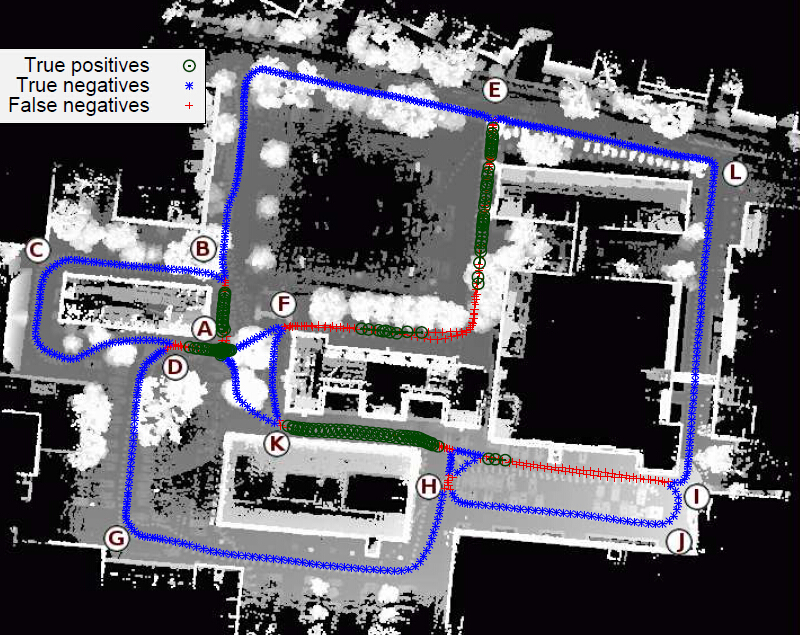
NDT(Normal Distribution Transform) 算法(与ICP对比)和一些常见配准算法的更多相关文章
- NDT 算法和一些常见配准算法
原文链接:http://ghx0x0.github.io/2014/12/30/NDT-match/ 目前三维配准中用的较多的是ICP迭代算法,需要提供一个较好的初值,同时由于算法本身缺陷,最终迭代结 ...
- NDT(Normal Distributions Transform)算法原理与公式推导
正态分布变换(NDT)算法是一个配准算法,它应用于三维点的统计模型,使用标准最优化技术来确定两个点云间的最优的匹配,因为其在配准过程中不利用对应点的特征计算和匹配,所以时间比其他方法快.下面的公式推导 ...
- 使用正态分布变换(Normal Distributions Transform)进行点云配准
正态分布变换算法是一个配准算法,它应用于三维点的统计模型,使用标准优化技术来确定两个点云间的最优的匹配,因为其在配准过程中不利用对应点的特征计算和匹配,所以时间比其他方法快.下面是PCL官网上的一个例 ...
- 3D点云配准算法简述
蝶恋花·槛菊愁烟兰泣露 槛菊愁烟兰泣露,罗幕轻寒,燕子双飞去. 明月不谙离恨苦,斜光到晓穿朱户. 昨夜西风凋碧树,独上高楼,望尽天涯路. 欲寄彩笺兼尺素.山长水阔知何处? --晏殊 导读: 3D点云 ...
- ICP(迭代最近点)算法
图像配准是图像处理研究领域中的一个典型问题和技术难点,其目的在于比较或融合针对同一对象在不同条件下获取的图像,例如图像会来自不同的采集设备,取自不同的时间,不同的拍摄视角等等,有时也需要用到针对不同对 ...
- 正态分布(Normal distribution)又名高斯分布(Gaussian distribution)
正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个在数学.物理及project等领域都很重要的概率分布,在统计学的很多方面有着重大的影 ...
- 论文阅读 Characterization of Multiple 3D LiDARs for Localization and Mapping using Normal Distributions Transform
Abstract 在这个文章里, 我们细致的比较了10种不同的3D LiDAR传感器, 用了一般的 Normal Distributions Transform (NDT) 算法. 我们按以下几个任务 ...
- Generalized normal distribution and Skew normal distribution
Density Function The Generalized Gaussian density has the following form: where (rho) is the " ...
- ICP算法(Iterative Closest Point迭代最近点算法)
标签: 图像匹配ICP算法机器视觉 2015-12-01 21:09 2217人阅读 评论(0) 收藏 举报 分类: Computer Vision(27) 版权声明:本文为博主原创文章,未经博主允许 ...
随机推荐
- ThreadLocal<T>的是否有设计问题
一.吐槽 ThreadLocal<T>明显是.NET从JAVA中来的一个概念,但是这种设计是否出现了问题. 很明显,在JAVA中threadLocal直接是Thread的成员,当然随着th ...
- PowerShell 操作 Azure SQL Active Geo-Replication 实战
<Azure SQL Database Active Geo-Replication简介>一文中,我们比较全面的介绍了 Azure SQL Database Active Geo-Repl ...
- 纯C#的ini格式配置文件读写
虽然C#里都是添加app.config 并且访问也很方便 ,有时候还是不习惯用他.那么我们来做个仿C++下的那种ini配置文件读写吧,其他人写的都是调用非托管kernel32.dll.我也用过 但是感 ...
- 自己动手写计算器v1.1
这个改动主要是使用工厂模式替代了简单工厂模式,这样做的好处是如果以后我们要扩充其他运算时,就不用总是去修改工厂类, 这是可以采取工厂模式,主要是将原来简单工厂类的逻辑判断分离出来,将它作为一个借口,与 ...
- shell编程
最吸引人的莫过于及时看到成果的努力,echo就是最好的初学者反馈函数,因为它的存在你可以及时的打印出结果. 1.分支 if[ ]:then elif ;then else fi 2.简单的循环,循环是 ...
- JSON总结(二)——google-gson
gson是一个google的开源项目,支持多种JSON方法,这里主要讲解如何使用gson将json转换成javaBean. maven坐标 <dependency> <groupId ...
- ABP Zero示例项目登录报错“Empty or invalid anti forgery header token.”问题解决
ABP Zero项目,登录时出现如图"Empty or invalid anti forgery header token."错误提示的解决方法: 在 WebModule.cs的P ...
- transformjs玩转星球
如你所见.这篇就是要讲下使用transformjs制作星球的过程.你也可以无视文章,直接去看源码和在线演示: 源码 | 在线演示 代码100行多一点,直接看也没有什么压力.下面分几步讲解下. 生成球上 ...
- Microsoft Dynamics CRM 2013 Js Odata 查询
实现功能: 在新建记录时,(大区,省区,城市)的值默认为当前用户的值.tips:字段均为lookup类型; function Default_region(){ var fromtype=Xrm. ...
- MBTiles
MBTiles Specification MBTiles is a specification for storing tiled map data in SQLite databases for ...
