B树和B+树详解

一 B树

1.B树的定义：B树（B-tree）是一种树状数据结构，它能够存储数据、对其进行排序并允许以O(log n)的时间复杂度运行进行查找、顺序读取、插入和删除的数据结构。B树，概括来说是一个节点可以拥有多于2个子节点的二叉查找树。

2.B树的特征：

• 根节点至少有两个子节点
• 每个中间节点都包含k-1个元素和k个孩子，其中 m/2 ≤ k ≤ m （m为树的阶）
• 每个叶子节点都包含k-1个元素，其中 m/2 ≤ k ≤ m （m为树的阶）
• 每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域划分（一个结点有k个孩子时，必有k-1个元素才能将子树中所有元素划分为k个子集）

3.B树的操作

3.1 B树的查找：如下图，查询元素8

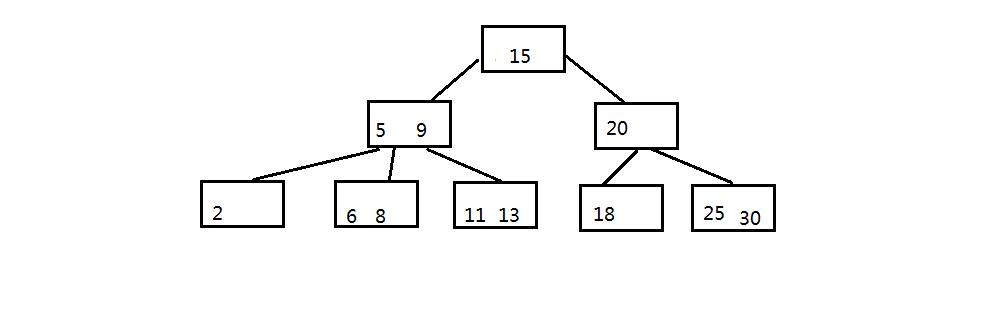
第一次磁盘IO：把15所在节点读到内存中，然后与8做比较，小于15，找到下一个节点（5和9对应的节点）

第二次磁盘IO：把5和9所在的节点读到内存中，然后与8做比较，5<8<9，找到下一个节点（6和8对应的节点）

第三次磁盘IO：把6和8所在节点读到内存中，然后与8做比较，找到了元素8

3.1 B树的插入： 将元素7插入下图中的B树

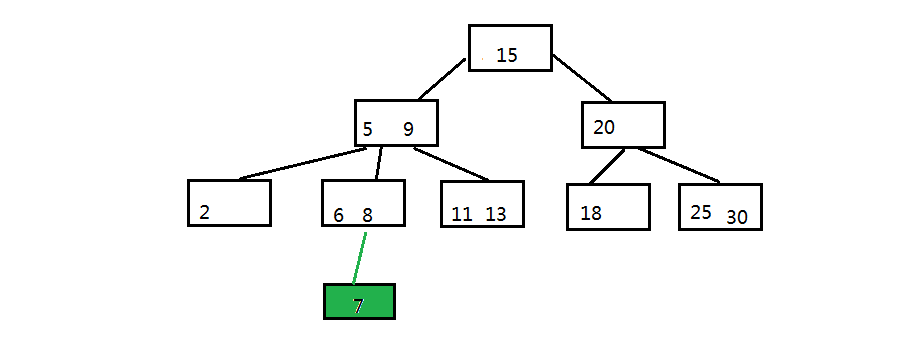
步骤一：自顶向下查找元素7应该在的位置，即在6和8之间

步骤二：三阶B树中的节点最多有两个元素，把6 7 8里面的中间元素上移（中间元素上移是插入操作的关键）

步骤三：上移之后，上一层节点元素也超载了，5 7 9中间元素上移，现在根节点变为了 7 15

步骤四：要对B树进行调整，使其满足B树的特性，最终如下图：

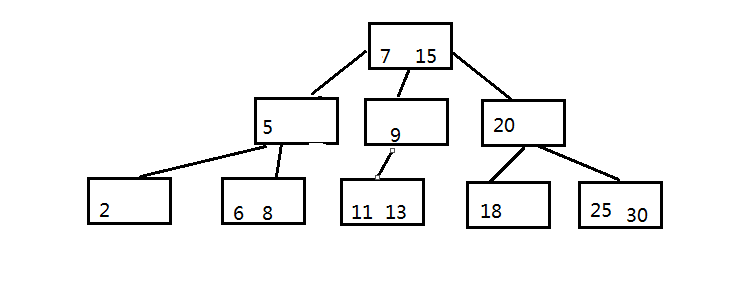
二 B+树 

B+树是B树的一种变形体，它与B树的差异在于：

• 有K个子节点的节点必然有K个关键码
• 非叶节点仅具有索引作用，元素信息均存放在叶节点中
• 树的所有叶节点构成一个有序链表，可以按照关键码排序的次序遍历全部记录

B+树的优势：

• 由于B+树在内部节点上不包含数据信息，因此在内存页中能够存放更多的key。 数据存放的更加紧密，具有更好的空间局部性。因此访问叶子节点上关联的数据也具有更好的缓存命中率。

• B+树的叶子节点都是相连的，因此对整棵树的遍历只需要一次线性遍历叶子节点即可。而且由于数据顺序排列并且相连，所以便于区间查找和搜索。而B树则需要进行每一层的递归遍历。相邻的元素可能在内存中不相邻，所以缓存命中性没有B+树好。

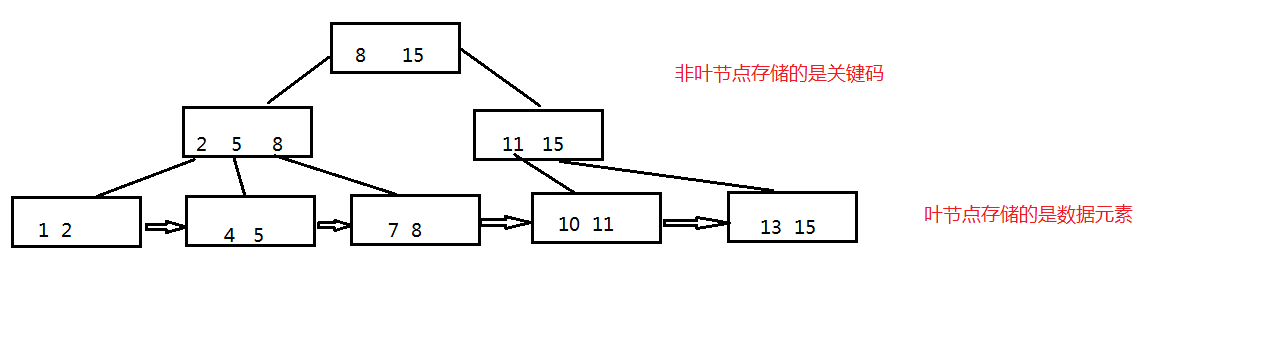
总结：我们知道二叉查找树的时间复杂度是Ｏ(logN)，效率已经足够高。为什么出现B树和B+树呢？当大量数据存储在磁盘上，进行查询操作时，需要先将数据加载到内存中（磁盘IO操作），而数据并不能一次性全部加载到内存中，只能逐一加载每个磁盘页（对应树的一个节点），并且磁盘IO操作很慢，平衡二叉树由于树深度过大而造成磁盘IO读写过于频繁，进而导致效率低下。为了减少磁盘IO的次数，就需要降低树的深度，那么就引出了B树和B+树：每个节点存储多个元素，采用多叉树结构。这样就提高了效率，比如数据库索引，就是存储在磁盘上，采用的就是B+树的数据结构。