Graph图总结

将COMP20003中关于Graph的内容进行总结，内容来自COMP20003，中文术语并不准确，以英文为准。

---

Graph G = {V, E}

　　顶Vertices V: can contain information

　　边Edges E (links between vertices): can have direction and/or weight

种类：

• 　　有向图(directed graph)：边(edge)有方向。
  • 弱有向连接图Weakly connected directed graph：将有向的边替换成无向的边后能得到无向连通图。

　　　　

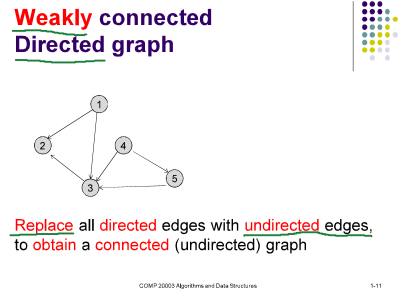
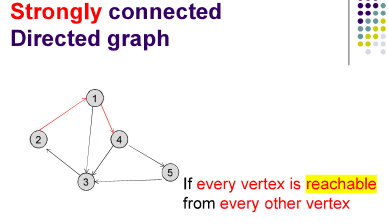
• • 强有向连接图Strongly connected directed graph：在有向图中，任意顶通过边到达任意顶。

　　　　

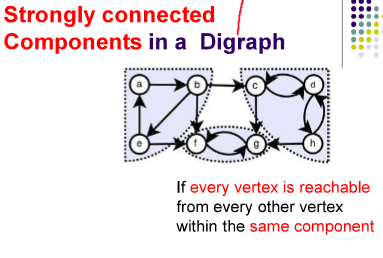
• • • Strongly connected components in a directed graph:在同一区域(component)的顶可以到达所有同一区域的顶。

　　　　　　　　

• 　　无向图(undirected graph)：边(edge)没有方向。
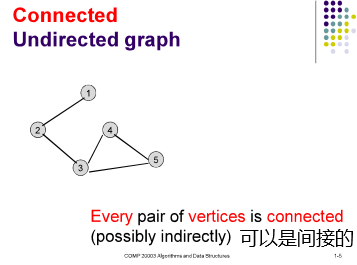
  • 无向连通图Connected Undirected graph: 任意的顶均可通过边连接到其他顶，包括间接。

　　　　

• • 无向非连通图Unconnected Undirected graph:即不是无向连通图Connected Undirected graph。

　　　　

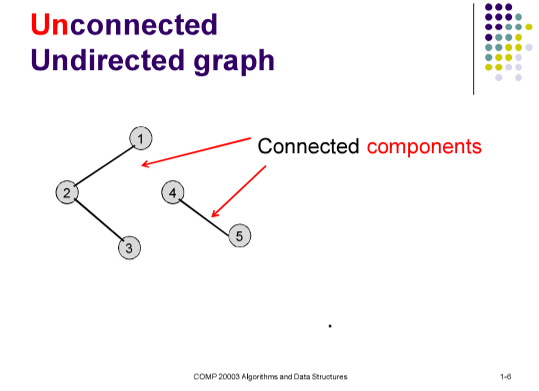
完全图Complete graph:每个顶能直接到其他顶。对于无向图至少需要V(V-1)/2个顶，有向图至少需要V（V - 1）个顶。

---

用数据结构表示：

用二维数组（Matrix）表示：

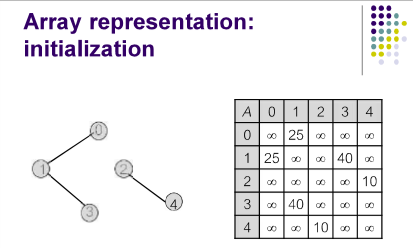
注意：未连接用无穷大表示，而不是用0表示。

复杂度O(V²)

用链表表示：

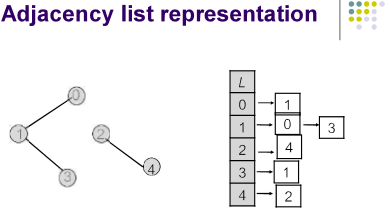
复杂度O(V + E)

---

图的遍历Traversal

Depth-first search(DFS)深度优先搜索，使用stack实现，基于stack先进后出的特性。

Breadth first search(BFS)广度优先搜索，使用queue实现，基于queue先进先出的特性。

---

图的拓扑：应用于有向无环图（Directed Acyclic Graphs，简称DAG）

　　Topological sort: a partial ordering that fulfils certain constraints. All edges e(i, j) go in horizontal i -> j direction

　　                          变成水平排列，只能从左边指向右边。

　　

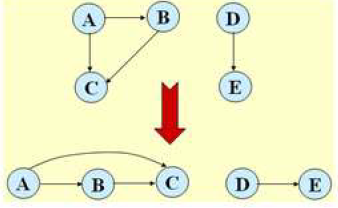
　　拓扑涉及的概念：

　　　　indegree：该顶被边到达的次数。

　　　　outdegree：由该顶开始边连接的次数。

　　能有拓扑结构，DAG图必须满足有一个source(indegree为0)和sink(outdegree为0)。

　　如果在DAG图中存在汉密尔顿路径(Hamiltonian path，即从某个顶开始通过边不重复的经过所有点的路径，想想游戏一笔画)，则该拓扑是唯一的。

　　代码：https://github.com/Will-Zhu-27/Algorithms-and-Data-Structures/tree/master/graph/Topological%20sort

---

算法：

Dijkstra's algorithm for single source shortest path

Dijkstra单源最短路径算法：一个顶到其他顶的最短路径。

基于Greedy algorithm: 最短路径中的子路径也是最短路径，即A到Y的最短路径经过X，那么该路径中从A到X的部分是A到X的最短路径。

假定没有负值的边。

使用优先队列priority queue。

步骤：

　　使用变量数组dist记录从目标定到该顶的最短距离，数组pred记录经过该顶的前一个顶，edgeWeight(a, b)：顶a到顶b边的值。

1. 1. 将dist自己到自己为0，其余最大(MAX_INT)。pred均为NULL。
   2. 将所有顶装入优先队列，按照对应的dist值的大小为优先度。
   3. 当优先队列不为空时，pop一个顶a，为空则结束。
   4. LOOP：如果dist[a] + edgeWeight(a, b) < dist[b]，b为跟顶a有边连接的顶，则更新顶b的信息：dist[b] = dist[a] + edgeWeight(a, b)，pred[b] = a，更新优先队列中的顺序(也可pop时再根据有限度pop)。
   5. 步骤3。

　　　　复杂度分析：

　　　　

　　　　实现代码：https://github.com/Will-Zhu-27/Algorithms-and-Data-Structures/tree/master/graph/shortestPaths/dijkstra

Warshall algorithm for transitive closure -- unconnected directed graph

Warshall算法：用于判断有向图中顶与顶之间是否能通过边联通（包括间接的）。

　　用二维数组储存基础（直接）边连接的信息，使用三次循环。

　　

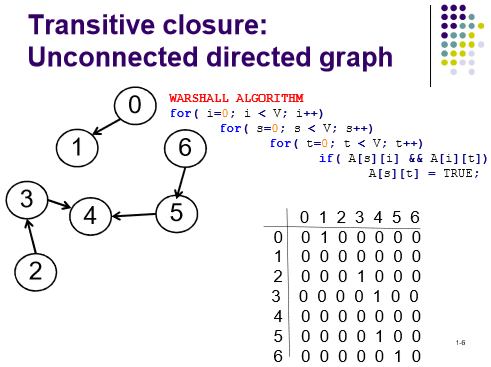
　　　　其中i for intermediate, s for source, t for to，循环变量怎么命名的并不重要，重要的是最外圈的循环变量i必须作为判断的中间变量，改变它的位置会导致算法出错。我的理解为：算法是基于贪心算法，

　　　　当循环到 i 时，就要得到通过 0 到 i 是否有最短路径，然后逐渐增大i达到在全部顶中的最短路径。此问题也可看在知乎上的这个问题的回答：https://www.zhihu.com/question/30955032

Floyd-Warshall algorithm for all pairs shortest paths

Floyd-Warshall算法：图中每个顶到其他顶的最短路径。

　　在Warshall的基础上稍作改变，二维数组储存的是顶之间weight的信息。

　　

同样的，最外圈的循环变量i必须作为判断的中间变量！另外用C实现时，虽然图里不连接用了∞表示， C中用 INT_MAX / 2 表示， 因为if 判断时会产生数据溢出问题。

要记录路径也只要加个二维数组记录即可。

复杂度：θ(V³)

代码：https://github.com/Will-Zhu-27/Algorithms-and-Data-Structures/tree/master/graph/AllPairsShorestPaths/Floyd-Warshall

Floyd-Warshall和dijkstra在计算all pairs shorest paths上的优劣：

　　循环V次dijkstra也可得到全部顶的最短路径，复杂度为：O((V² + V * E)logV)

　　Floyd-Warshall复杂度为θ(V³)。

　　对于sparse graph with positive edge weights（V>>E），Dijkstra用于all pair shortest path更好

　　　　对于dense graph with positive edge weights(E>>V) Floyd-Warshall更好

　　

---

最小生成树 Minimum Spanning Tree, MST

　　要求：

　　　　undirected weighted graphs

　　　　Graph must be connected   无向非连通图

　　MST特点：

　　　　包括所有的顶

　　　　minimum sum of edge weights，包含连接顶的边和最小，数量为V-1

　　　　MST中没有循环（cycles）。

　　简言之，使用最小weight的edge将所有顶连接到。

　　

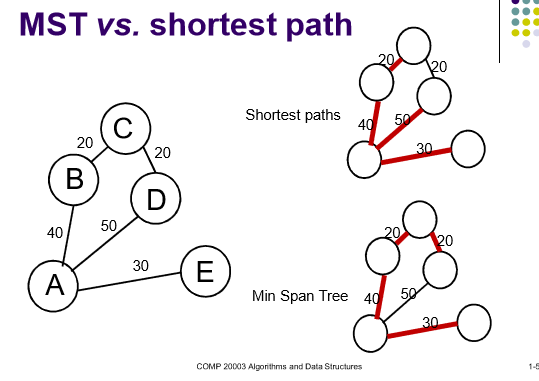
　　如果所有的edge的weight不同，那么MST是唯一的。

　　计算MST的算法有Prim和Kruskal。

　　Prim：通过添加下一个最近的顶完成MST。

　　　　需要使用优先队列。

　　　　

　　　　准备：dist[V]初值MAX，pred[V]初值NULL，inMst[V]初值FALSE。

　　　　步骤：

1. 1. 将某一顶 （随便那个）作为起始点root，dist[ root ] = 0。将全部顶enqueue优先队列，以dist为优先级。
   2. pop一个顶a，所有与a直接相连的顶b：如果inMst[b]==FALSE && a到b的edge < dist[b]，则更新dist[b]等于该edge，更新pred[b]=a，调整优先队列中的顺序。
   3. inMst[a] = TRUE;
   4. 优先队列为空->结束， 不为空->步骤2

　　　　若手工计算，以a为起始点为例，与a相连的有b和c，到b更短，选b。

　　　　

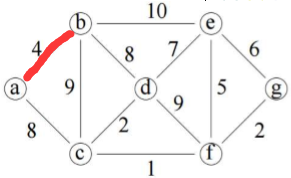
　　　　将a和b作为一个整体，与整体相连的有c、d、e，c和d到整体(最短)都是8，随便选一个，选c。

　　　　

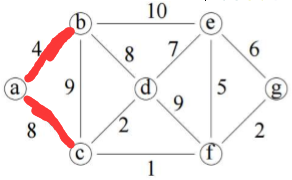
　　　　将a和b和c作为一个整体，与整体相连的有e、d、f，到整体最短的是f，选f。

　　　　

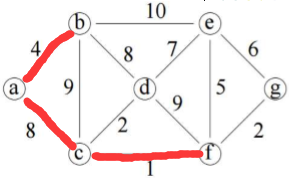
　　　　将a和b和c和f作为一个整体，与整体相连的有e、d、g，到整体最短的是d，选d。

　　　　

　　　　

　　　　将a和b和c和f和d作为一个整体，与整体相连的有e、g，到整体最短的是g，选g。

　　　　

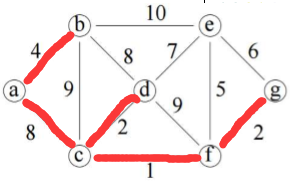
　　　　将a和b和c和f和d和g最为一个整体，与整体相连的有e，选e。

　　　　

　　　　复杂度分析：

　　

　　　　从算法步骤可以看出复杂度是与V有关的，所以Prim更适合dense graph（E>>V）。

　　　　代码：https://github.com/Will-Zhu-27/Algorithms-and-Data-Structures/tree/master/graph/Minimum%20Spanning%20Tree/Prim

　　Kruskal：通过添加最短的且不构成回路的边完成MST

　　　　需要使用优先队列和Union-find 结构。

　　　　Union-find 结构：所有的顶都各自为一个集合，如果因为E[a][b]（连接顶a和顶b）是mst中的话，则a和b所在的集合合并，可以以数组表示如下图。

　　　　

　　　　也可以用树的形式表示，以树的形式表示的话，在进行union合并操作时，注意时将小的树并入大的树中。

　　　　步骤：

　　　　　　1.将所有边根据weight入列优先队列。将所有顶装入union-find结构。

　　　　　　2.从优先队列中取出一条边E[a][b]（weight最小的）。

　　　　　　3.如果a和b在同一集合中，则步骤2。如果不再同一集合中，则a和b所在的集合合并，E是mst的一条边。

　　　　　　4.当mst边的数量< V - 1，步骤2。

　　　　若手工计算，以下图为例：

　　　　

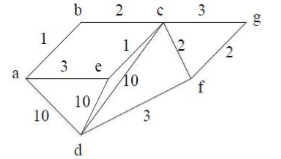
　　　　　　E[a][b](或者是E[c][e]，只要不构成回路，选哪个都行)为mst中的边。

　　　　　　

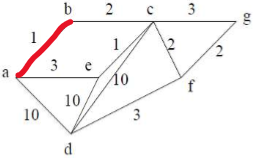
　　　　　　E[c][e]为mst中的边。

　　　　　　

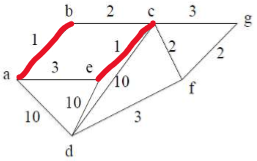
　　　　　　E[b][c]为mst中的边。

　　　　　　

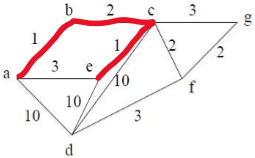
　　　　　　E[c][f]为mst中的边。

　　　　　　

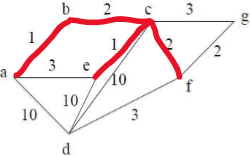
　　　　　　E[g][f]为mst中的边。

　　　　　　

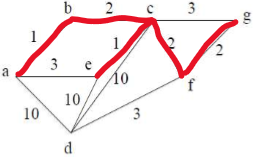
　　　　　　E[d][f]为mst中的边，不能是E[c][g]或E[a][e]会构成回路。

　　　　　　

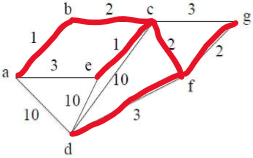
　　　　　　已经过所有的顶，mst完成。

　　　　代码：https://github.com/Will-Zhu-27/Algorithms-and-Data-Structures/tree/master/graph/Minimum%20Spanning%20Tree/Kruskal