利用PCA降维

参考：《机器学习实战》- Machine Learning in Action

一、 基本思想

 PCA(Principal Component Analysis)，主成分分析。是目前应用最为广泛的降维技术。

 什么是降维？举个例子：假设我们正通过电视观看体育比赛，显示器大概包含了100万像素，而球则可能是由较少的像素组成的，比如一千个像素。大部分体育比赛中，我们关注的是给定时刻球的位置。这个过程，人们就已经将数据从一百万维降低到了三维。

 考虑下图的大量数据点，如果要我们画一条直线，这条线要尽量可能覆盖这些点，很明显是直线B。

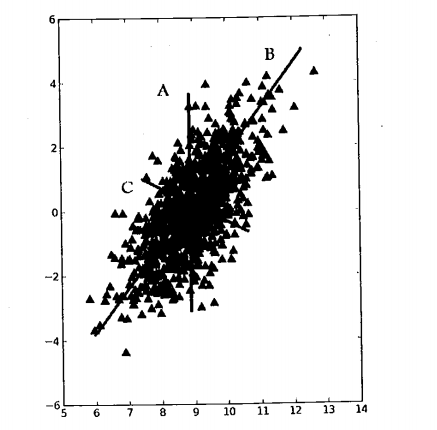
 现在，我们将坐标轴旋转，使得X轴平行于B直线，接下来是进行降维操作，结果如下：

 我们来分析下大致的流程：第一个主成分是从数据差异性最大的方向提取出来的，第二个主成分则来自于数据差异性次大的方向，并且该方向与第一个主成分方向正交。而通过数据集的协方差矩阵及其特征值分析，我们就可以求得这些主成分的值。

 大致流程如下：

• 去除平均值
• 计算协方差矩阵
• 计算协方差矩阵的特征值和特征向量
• 将特征值从大到小排序
• 保留最上面的N个特征向量
• 将数据转换到上述N个特征向量构建的新空间

二、 代码

# -*- coding:utf8 -*-
from numpy import *

def loadDataSet(fileName, delim='\t'):
	fr = open(fileName)
	stringArr = [line.strip().split(delim) for line in fr.readlines()]
	dataArr = [map(float, line) for line in stringArr]
	return mat(dataArr)

def pca(dataMat, topNfeet=9999999):
	meanVals = mean(dataMat, axis=0)
	meanRemoved = dataMat - meanVals
	covMat = cov(meanRemoved, rowvar=0)
	eigVals, eigVects = linalg.eig(mat(covMat))
	eigValInd = argsort(eigVals)
	eigValInd = eigValInd[:-(topNfeet+1):-1]
	redEigVects = eigVects[:,eigValInd]
    lowDDataMat = meanRemoved * redEigVects
    reconMat = (lowDDataMat * redEigVects.T) + meanVals
    return lowDDataMat, reconMat