【Codeforces 851D Arpa and a list of numbers】

Arpa的数列要根据GCD变成好数列。

·英文题，述大意：
      给出一个长度为n(n<=5000000)的序列,其中的元素a[i]<=10⁶,然后输入两个数x,y(x,y<=10⁹)现在有两种操作：①支付x的代价删除一个数。②支付y的代价将一个数加1。题目要求支付最少的代价，使得原序列所有元素的GCD不为1。

·分析：
      GCD不为1?那么就是说每个数至少有一个共同的非1因子。使所有数拥有同一个因子一定比使它们拥有两个相同因子容易，所以题目其实要求我们完成这个任务：对于某个因子a(就是一个数a)，若将原序列所有的数，通过上述操作，使得它们都含有a这个因子的代价和为W,求出所有a中W的最小值。

      根据上文结论，一个相同比两个相同容易，所以呢这个最优解的因子x一定是一个素数(如果是合数就拆成两个或两个以上的素数因子了啊)。

      观察数据，考虑怎样的时间复杂度能够承受：
      从这题来看，相比于元素个数5*10⁶,元素的范围10⁶是一个较小的值，这个值有两种时间复杂度思考：一种是O(N),一种是O(NlogN)对吧？对！

      我们来细看每个元素，如果我们当前枚举因子x(即目标是让所有元素都能够被它整除),对于它只有两种选择：(1)删除(2)通过加1操作使它变成最近的那个a的倍数。很明显，我们需要取舍一番。怎样正确而快速地决策呢？

       由于我们已知了x,y。那么一个数加几个1能够满足比删除这个数的代价小呢？当然是最多加[x/y]次啦 ，这里设T=[x/y](向下取整)。所以我们不妨枚举每一个x的倍数区间，下图所示：

那么对于每一个区间里的元素：

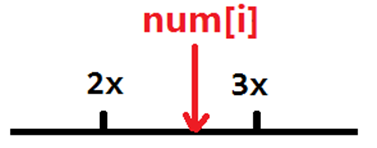
如果它向前走T步以内能够到达3*x，那么我们选择加1绝对比删除它的代价小。反之，我们就删除这个数。下面分别计算两种方案下代价：

       ①通过加一操作:(kx-num[i])*y

       ②通过删除操作:x

       因此，推广地说，如果这个区间[(k-1)*x,kx]内有e1个元素选择方案一,e2个元素选择方案二，那么代价W为:

  W=(kx*e1-Sum(num[i]))*x+e2*y(其中,Sum表示一方案的所有元素的和)

      据此，维护两个前缀数组：

      (1)sum[i]: 表示小于i的元素的个数

      (2)tot[i]:  表示小于i的元素的和

然后整个过程就是：预处理素数和前缀和，然后枚举计算每个素数x的最优代价。由于每次区间的长度变化，所以时间复杂度为O(nlogn)   

      代码在这里：    

 #include<stdio.h>
 #include<algorithm>
 #define ll long long
 #define go(i,a,b) for(int i=a;i<=b;i++)
 const int N=;int t,prime[N],n,a,sum[N],lim,T;
 ll x,y,ans,tot[N];
 void Prime()
 {
     bool no[N]={};lim=;
     go(i,,lim){if(!no[i])prime[++t]=i;
     go(j,,t)if(1ll*prime[j]*i<=lim){no[prime[j]*i]=;}else break;}
 }
 int main()
 {
     scanf("%d%I64d%I64d",&n,&x,&y);T=x/y;
     go(i,,n)scanf("%d",&a),sum[a]++,tot[a]+=a;Prime();
     go(i,,lim+prime[t])sum[i]+=sum[i-],tot[i]+=tot[i-];ans=1e18;
     go(j,,t)
     {
         int l,r=;ll res=;while(r<=lim)
         {
             l=r;r+=prime[j];int p=std::max(l,r-T-);
             res+=1ll*(sum[p]-sum[l])*x+(1ll*r*(sum[r]-sum[p])-(tot[r]-tot[p]))*y;
             if(r>lim)break;
         }
         ans=std::min(ans,res);
     }
     printf("%I64d\n",ans);return ;
 }//Paul_Guderian

有一天这首歌会变老就像老杨树上的枝芽

可我还会一遍遍歌唱它如同我的生命。————汪峰《我爱你中国》