应用统计学：

s检验是检验否符合正态，而k-S检验是检验否符合一种分布。

已知分布便知道参数，知道参数不知道分布。

适应性检验

多项式分布的情况如下例：

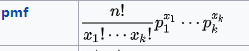
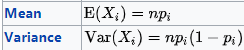
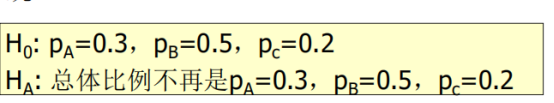
二项分布是多项式分布一种情况，所以就是上式中只有两个概率

独立性检验：PAB=PAPB

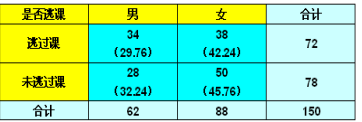
其中，29.76由假设独立后比例算得。

格式：

是右尾检验，但是因为SPSS中只提供双尾检验所以显示如下图，但是还是可以从双尾的角度考虑：

Person Chi-Square适用情况是N>40 person ei>1

Cintinuity correction 适用:2X2

Likelihood Ratio 适用N<40

Fisher‘s Exact Test’适用N<40 2X2

两个因素的相关性度量：

φ系数的范围是（0,1），并且越接近1关系越强

对于非2X2做修正使用Cramer’s V检验，且（0,1）越接近1关系越强

列联系数：2X2：

 

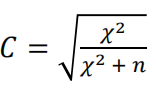
s检验|k-S检验|适应性检验|独立性检验|Cintinuity correction |Fisher‘s Exact Test|Likelihood Ratio|Person Chi-Square|φ系数|Cramer’s V|列联系数的更多相关文章

  1. Fisher's exact test( 费希尔精确检验)

    Fisher's exact test[1][2][3] is a statistical significance test used in the analysis ofcontingency t ...

  2. SAS学习笔记25 t检验（单个样本t检验、配对样本t检验、两个独立样本t检验及方差不齐时的t'检验）

    根据研究设计和资料的性质有单个样本t检验.配对样本t检验.两个独立样本t检验以及在方差不齐时的t'检验 单样本t检验 单样本t检验(one-sample t-test)又称单样本均数t检验,适用于样本 ...

  3. spss-非参数检验-K多个独立样本检验（ Kruskal-Wallis检验）案例解析

    今天和大家一起探讨和分下一下SPSS-非参数检验--K个独立样本检验 ( Kruskal-Wallis检验). 还是以SPSS教程为例: 假设:HO:   不同地区的儿童,身高分布是相同的 H1: 不 ...

  4. SPSS-Friedman 秩和检验-非参数检验-K个相关样本检验 案例解析

    三人行,必有我师,是不是真有我师?三种不同类型的营销手段,最终的营销效果是否一样,随即区组秩和检验带你进入分析世界 今天跟大家讨论和分享一下:spss-Friedman 秩和检验-非参数检验-K个(多 ...

  5. 《R语言实战》读书笔记 第七章--基本统计分析

    在导入数据并且将数据进行组织和初步可视化以后,需要对数据进行分布探索和两两关系分析等.主要内容有描述性统计分析.频数表和列联表.相关系数和协方差.t检验.非参数统计. 7.1描述性统计分析 7.1.1 ...

  6. T检验与F检验的区别_f检验和t检验的关系

    1,T检验和F检验的由来 一般而言,为了确定从样本(sample)统计结果推论至总体时所犯错的概率,我们会利用统计学家所开发的一些统计方法,进行统计检定. 通过把所得到的统计检定值,与统计学家建立了一 ...

  7. 通俗理解T检验和F检验

    来源: http://blog.sina.com.cn/s/blog_4ee13c2c01016div.html   1,T检验和F检验的由来 一般而言,为了确定从样本(sample)统计结果推论至总 ...

  8. 通俗理解T检验与F检验的区别【转】

    转自:http://blog.sina.com.cn/s/blog_4ee13c2c01016div.html1,T检验和F检验的由来一般而言,为了确定从样本(sample)统计结果推论至总体时所犯错 ...

  9. 统计学常用概念：T检验、F检验、卡方检验、P值、自由度

    1,T检验和F检验的由来 一般而言,为了确定从样本(sample)统计结果推论至总体时所犯错的概率,我们会利用统计学家所开发的一些统计方法,进行统计检定. 通过把所得到的统计检定值,与统计学家建立了一 ...

随机推荐

  1. Java学习十七

    学习内容: 1.Java字符串类 1.在utf-8编码下,每个汉字占三个字节 2.字符串和byte数组之间的相互转换 将字符串转换为byte数组 byte[] arrs = str.getBytes( ...

  2. Spring Cloud Zuul 网关服务的fallback

    当我们的zuul进行路由分发时,如果后端服务没有启动,或者调用超时,这时候我们希望Zuul提供一种降级功能,而不是将异常暴露出来. Spring cloud zuul提供这种降级功能,操作步骤如下: ...

  3. 6.react 基础 - 关于 react 开发 的原则

    1. 声明式开发 通过绑定元素 在数据变更时 对元素进行动态渲染 2. 可以与其他框架并存 不在React的绑定元素内, 可以使用其他框架 如 ( vue jQuery 等 ) 进行元素操作 3. 组 ...

  4. PHP学习之-文件上传

    一.PHP文件上传 HTML部分 <form action="file_big.php" method="post" enctype="mult ...

  5. jQuery如何给DOM添加ID

    ID每个元素只能有一个,ID名同一页面也不能重复,addID方法是不需要的,和其他属性一样用attr方法就行了, $(singleTarget).attr('id','idName'); 更简单的 $ ...

  6. Mac技巧-如何切换至 Mac 地图应用的卫星视图模式

    如何切换至Mac地图应用的卫星视图模式?很多刚接触MAC电脑的小伙伴并不是很清楚,今天MACW小编就教教大家切换至 Mac 地图应用的卫星视图模式该怎么做.原文:https://www.macw.co ...

  7. EXCEL启动慢

    启动太慢,一般是加载项的问题. 1.点击文件-EXCEL选项 2. 找到加载项,一般是COM加载项 3.选择com加载项 4.然后我出现了无法更改的情况,于是,我做了以下调整,进入office安装目录 ...

  8. 吴裕雄--天生自然 PHP开发学习：MySQL 预处理语句

    <?php $servername = "localhost"; $username = "root"; $password = "admin& ...

  9. ubuntu 编译VLC3.0.0

    参考链接 https://blog.csdn.net/u014755412/article/details/78874038 https://www.cnblogs.com/wpjamer/p/919 ...

  10. [Algo] 253. Longest Substring Without Repeating Characters

    Given a string, find the longest substring without any repeating characters and return the length of ...