java实现第四届蓝桥杯公式求值

公式求值

输入n, m, k，输出图1所示的公式的值。其中C_n^m是组合数，表示在n个人的集合中选出m个人组成一个集合的方案数。组合数的计算公式如图2所示。

输入的第一行包含一个整数n；第二行包含一个整数m，第三行包含一个整数k。

计算图1所示的公式的值，由于答案非常大，请输出这个值除以999101的余数。

【样例输入1】

3

1

3

【样例输出1】

162

【样例输入2】

20

10

10

【样例输出2】

359316

【数据规模与约定】

对于10%的数据，n≤10，k≤3；

对于20%的数据，n≤20，k≤3；

对于30%的数据，n≤1000，k≤5；

对于40%的数据，n≤10^7，k≤10；

对于60%的数据，n≤10^15，k ≤100；

对于70%的数据，n≤10^100，k≤200；

对于80%的数据，n≤10^500，k ≤500；

对于100%的数据，n在十进制下不超过1000位，即1≤n<10^1000，1≤k≤1000，同时0≤m≤n，k≤n。

【提示】

999101是一个质数；

当n位数比较多时，绝大多数情况下答案都是0，但评测的时候会选取一些答案不是0的数据；

资源约定：

峰值内存消耗（含虚拟机） < 128M

CPU消耗 < 2000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意：不要使用package语句。不要使用jdk1.6及以上版本的特性。

注意：主类的名字必须是：Main，否则按无效代码处理。

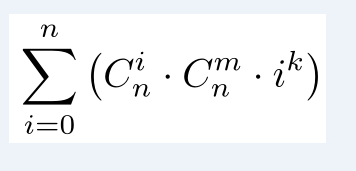
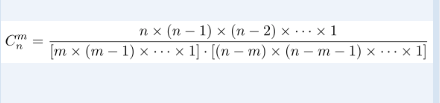
这道题附上一个思路方便读者了解

Lucas定理加上一些数学处理转换。直接给大家个链接吧http://tieba.baidu.com/p/2832505865。重点可以看看

十四楼对这道题的处理方法，还是不太懂的话可以草稿纸上演算演算。注意dp[i][j]代表第i次求导后(x^j)*(1+x)(n-j)的系数。然后具体写代码的时候，方法返回类型尽量处理为long，能取模就取模，尽量少用大数直接加减乘除运算操作，不然后面的数据会超时（我一开始就直接用大数写，最后两个点超时了，前面几个点也比较灵异地出现了错误答案）。其他标程逆元部分似乎是利用费马小定理，然后a^(p-2)模p为a模p的逆元，而我是直接利用扩展欧几里得求a模p的逆元。对了，还要注意lucas定理利用时，如果c(n%p,m%p)中n%p<m%p，则值应直接返回0而不是1(这就是那个测试点的问题所在)

import java.math.BigInteger;
import java.util.Scanner;
class Number {
	long x,y,dd;

	/**
	 * @param x
	 * @param y
	 * @param dd
	 */
	public Number(long x, long y, long dd) {
		super();
		this.x = x;
		this.y = y;
		this.dd = dd;
	}

	/**
	 *
	 */
	public Number() {
		super();
		// TODO Auto-generated constructor stub
	}

}
public class Main {
	static BigInteger n, m;
	static int k;
	static long monum = 999101;
	static BigInteger mobig = new BigInteger("999101");
	static BigInteger big2 = new BigInteger("2");
	static long ansnum1,ans;
	static long dp[][], bignum[], subnum[];
	static long fact[];
    private static Number gcd(long a,long b) {
	  if (b==0) return new Number(1,0,a);
	  Number number=gcd(b, a%b);
	  long x=number.y;
	  long y=number.x-(a/b)*number.y;
	  long dd=number.dd;
	  return new Number(x,y,dd);
    }
    private static long mod_inverse(long num) {
    	if (num==0) return 0;
    	Number number=gcd(num, monum);
    	long x=(number.x+monum)%monum;
    	return x;
    }
	private static long cal(BigInteger num) {
		if (num.equals(BigInteger.ZERO)) return 1;
		if (num.equals(BigInteger.ONE)) return 2;
		long mnum = cal(num.divide(big2));
		mnum = mnum*mnum%monum;
		BigInteger mo = num.mod(big2);
		if (mo.equals(BigInteger.ONE))
			mnum=mnum*2%monum;
		return mnum;
	}

	private static void init() {
		fact = new long[(int) (monum + 1)];
		fact[0] = 1;
		for (int i = 1; i <= monum; i++)
			fact[i]=(fact[i-1]*(long)i)%monum;
	}
	private static long calc(int n,int m) {
		if (n<m) return 0;
		long mo=fact[m]*fact[n-m]%monum;
		long divnum=mod_inverse(mo);
		long res=fact[n]*divnum%monum;
		return res;
	}
    private static long lucas(BigInteger n,BigInteger m){
    	if (m.equals(BigInteger.ZERO)) return 1;
    	int nmo=n.mod(mobig).intValue();
    	int mmo=m.mod(mobig).intValue();
    	return calc(nmo, mmo)*lucas(n.divide(mobig),m.divide(mobig))%monum;
    }
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner reader = new Scanner(System.in);
		n = reader.nextBigInteger();
		m = reader.nextBigInteger();
		k = reader.nextInt();
		BigInteger kbig=new BigInteger(String.valueOf(k));
		dp = new long[k + 1][k + 1];
		dp[0][0]=1;
		long mon=n.mod(mobig).longValue();
		for (int i = 0; i <= k - 1; i++)
			for (int j = 0; j <= i; j++) {
				dp[i + 1][j] = (dp[i+1][j]+(long)j*dp[i][j])%monum;
				dp[i + 1][j + 1] =(dp[i+1][j+1]+(long)(mon-j+monum)*dp[i][j])%monum;
			}
		long mulnum =cal(n.subtract(kbig));
		for (int i = k; i >= 0; i--) {
			ansnum1 =(ansnum1+dp[k][i]*mulnum)%monum;
			mulnum = (mulnum*2)%monum;
		}
		init();
		ans=ansnum1*lucas(n, m)%monum;
		System.out.println(ans);
	}

}