题解 P2070 【刷墙】

前言

\(ZHK\)私人博客体验更佳

这道题目，\(n<=10^5\)，显然在暗示我们使用\(n \log n\)的做法，我就是用了一个简单的贪心，通过了此题。

正文

在这道题中，我们发现，可以把 \(Bessie\) 每次走的路看成是对序列的一段区间染色。

for(int i=1;i<=n;i++){
	int x;char y;
	read(x);cin>>y;
	a[i].l=position;
	if(y=='L')position-=x;//Bessie往左走
	else position+=x;//Bessie往右走
	a[i].r=position;
	if(a[i].l>a[i].r)swap(a[i].l,a[i].r);
}

这里的 \(a\)数组是一个结构体——\(node\)

const int MAXN=1e5+10;
struct node{
	int l,r;//每次染色的左端点和右端点
	bool operator<(const node&b)const{
		return l<b.l;//按左端点从小到大排序
	}
}a[MAXN];

之后，我们就要说真正的思路了，我们对于 \(a\) 序列排序后，会有这样一个画面。

我们定义两个变量——\(lft\)和\(rgt\)，记录可能区间的左端点和右端点。

这里面我们记录的是有可能和下面相交的区间，什么意思？比如那张图，我们标一下号

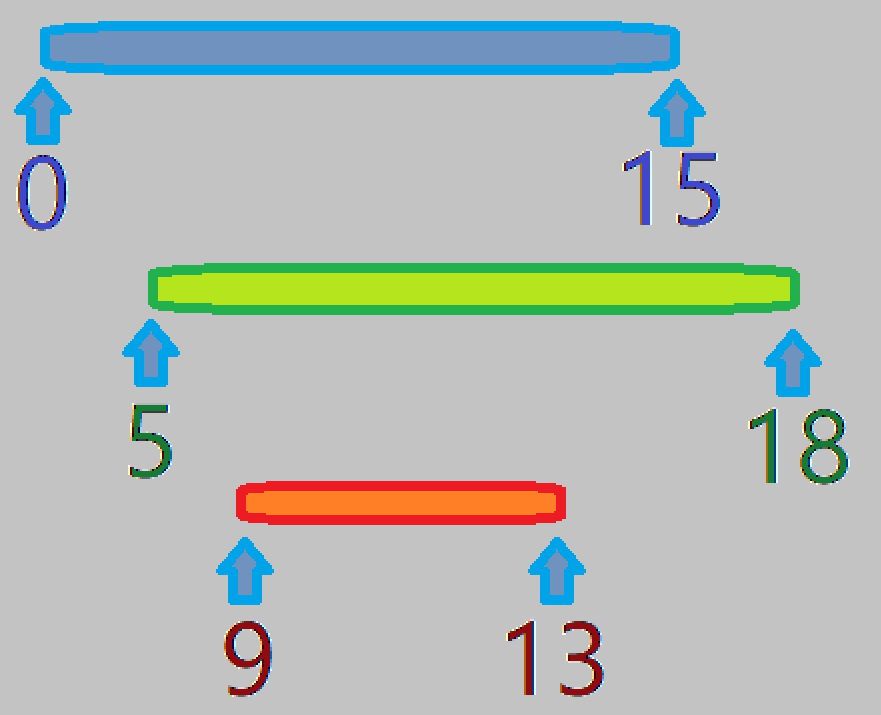
当我么扫描第 \(1\) 个区间时，我们发现，之后有可能被覆盖到的区间是 \(lft=0,rgt=15\)。

当我们继续扫描，到第 \(2\) 个区间时，我们发现，之后可能被覆盖到的区间是 \(lft=15,rgt=18\)。

可能有人会问，\(5\)~\(15\) 这段消失，我们还能理解，但是为什么 \(0\)~\(5\) 这段也没了呢，因为第 \(2\) 个区间的\(l\)都大约 \(0\) 了，之后的区间肯定就更大于 \(0\) 了，我们是按 \(l\) 从小到大排序的啊。

所以，我可以放一下代码了：

for(int i=2;i<=n;i++)
	if(a[i].r>lft){//如果跟可能被覆盖到的区间有交
		a[i].l=max(a[i].l,lft);//这里是使得之后的代码可以少写一点，因为显然，a[i].l<lft，a[i].l~lft这1段也没有用了
		if(a[i].r>rgt){//比之前的右端点大
			ans+=rgt-a[i].l;//从rgt到a[i].l
			lft=rgt;//之前的右端点显然就是左端点，显然，新的可能被覆盖到的区间就是之前的rgt~a[i].r
			rgt=a[i].r;//更新右端点
		}else{//比之前的右端点小
			ans+=a[i].r-a[i].l;//从a[i].r到a[i].l
			lft=a[i].r;//更新左端点
		}
	}

总结

我们先来看一下完整的代码：

#include <bits/stdc++.h>
using namespace std;
template<typename T>inline void read(T &FF){
    T RR=1;FF=0;char CH=getchar();
    for(;!isdigit(CH);CH=getchar())if(CH=='-')RR=-1;
    for(;isdigit(CH);CH=getchar())FF=(FF<<1)+(FF<<3)+(CH^48);
    FF*=RR;
}//快读
template<typename T>void write(T x){
    if(x<0)putchar('-'),x*=-1;
    if(x>9)write(x/10);
    putchar(x%10+48);
}//快写
const int MAXN=1e5+10;
struct node{
	int l,r;//每次染色的左端点和右端点
	bool operator<(const node&b)const{
		return l<b.l;//按左端点从小到大排序
	}
}a[MAXN];
int position,ans,lft,rgt,n;
int main(){
	read(n);
	for(int i=1;i<=n;i++){
		int x;char y;
		read(x);cin>>y;
		a[i].l=position;
		if(y=='L')position-=x;//Bessie往左走
		else position+=x;//Bessie往右走
		a[i].r=position;
		if(a[i].l>a[i].r)swap(a[i].l,a[i].r);
	}sort(a+1,a+n+1);//排序
	lft=a[1].l;rgt=a[1].r;//给lft和rgt赋上初值
	for(int i=2;i<=n;i++)
		if(a[i].r>lft){//如果跟可能被覆盖到的区间有交
			a[i].l=max(a[i].l,lft);//这里是使得之后的代码可以少写一点，因为显然，a[i].l<lft，a[i].l~lft这1段也没有用了
			if(a[i].r>rgt){//比之前的右端点大
				ans+=rgt-a[i].l;//从rgt到a[i].l
				lft=rgt;//之前的右端点显然就是左端点，显然，新的可能被覆盖到的区间就是之前的rgt~a[i].r
				rgt=a[i].r;//更新右端点
			}else{//比之前的右端点小
				ans+=a[i].r-a[i].l;//从a[i].r到a[i].l
				lft=a[i].r;//更新左端点
			}
		}
	write(ans);//输出
	return 0;
}

补充一下正确性证明：

实际上作者想到这个方法的时候觉得显然是对的

其实主要就是为什么要 \(lft=a[i].r\) 可能有人对此有点问题，我来解释一下

\(\therefore\) 我们是按从小到大对 \(a\) 数组进行排序，也就是 \(a[i+1].l \geq a[i].l\)，而 \(a[i].l>lft\)

\(\because\) \(a[i+1].l>lft\)。