凸包问题 Graham Scan

2020-01-09 15:14:21

凸包问题是计算几何的核心问题，并且凸包问题的研究已经持续了好多年，这中间涌现出了一大批优秀的算法。

凸包问题的最优解法是Graham Scan算法，该算法可以保证在最差情况下也能在O(nlogn)的时间复杂度求出结果。

Graham Scan算法的核心思路有两个步骤：

1. 预处理：将所有的点按照某个给定的点根据夹角进行排序；

2. 在排序好的结果上，按照顺序逆时针依次进行判断（to left test），将符合条件的节点加入栈中；

在具体实现的时候有一个非常好用的trick，就是不直接对夹角进行排序，而是假定在 +inf 和 -inf 有两个点，那么我们只需要根据x轴进行排序，就可以得到它们相对于两个无穷远点的夹角排序。

这样我们就可以直接使用第二步的递推迭代得到upper hull和lower hull，最后将这两个结果拼接起来就是最终的结果。

下面根据一条leetcode的题目来具体看下代码实现。

问题描述：

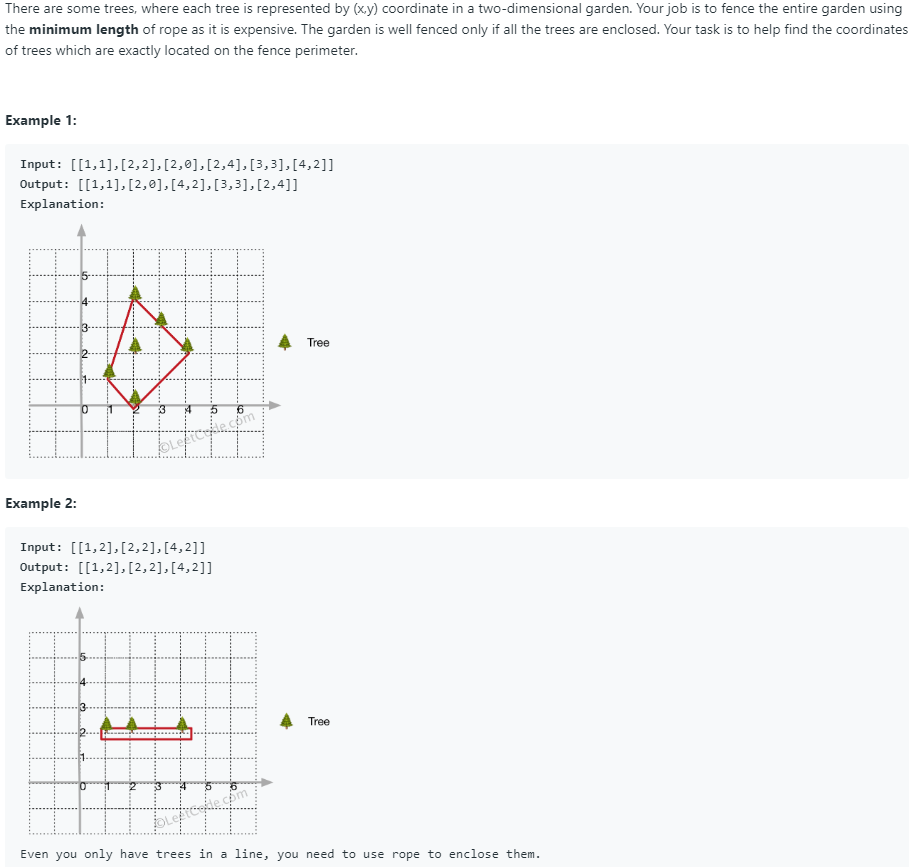
问题求解：

    public int[][] outerTrees(int[][] points) {
        if (points.length <= 3) return points;
        int n = points.length;
        Arrays.sort(points, new Comparator<int[]>(){
            public int compare(int[] o1, int[] o2) {
                return o1[0] == o2[0] ? o1[1] - o2[1] : o1[0] - o2[0];
            }
        });
        Stack<int[]> upper = new Stack<>();
        Stack<int[]> lower = new Stack<>();
        Stack<int[]> left = new Stack<>();

        upper.add(points[n - 1]);
        upper.add(points[n - 2]);
        lower.add(points[0]);
        lower.add(points[1]);

        for (int i = 0; i < n - 2; i++) left.add(points[i]);
        while (!left.isEmpty()) {
            int[] curr = left.pop();
            if (upper.size() == 1) {
                upper.add(curr);
                continue;
            }
            int[] p2 = upper.pop();
            int[] p1 = upper.pop();
            if (to_left_test(p1, p2, curr)) {
                upper.add(p1);
                upper.add(p2);
                upper.add(curr);
            }
            else {
                upper.add(p1);
                left.add(curr);
            }
        }

        for (int i = n - 1; i > 1; i--) left.add(points[i]);
        while (!left.isEmpty()) {
            int[] curr = left.pop();
            if (lower.size() == 1) {
                lower.add(curr);
                continue;
            }
            int[] p2 = lower.pop();
            int[] p1 = lower.pop();
            if (to_left_test(p1, p2, curr)) {
                lower.add(p1);
                lower.add(p2);
                lower.add(curr);
            }
            else {
                lower.add(p1);
                left.add(curr);
            }
        }

        Set<int[]> set = new HashSet<>();
        set.addAll(upper);
        set.addAll(lower);
        int[][] res = new int[set.size()][2];
        int idx = 0;
        for (int[] p : set) {
            res[idx][0] = p[0];
            res[idx][1] = p[1];
            idx += 1;
        }
        return res;
    }

    private boolean to_left_test(int[] p1, int[] p2, int[] p3) {
        return p1[0] * p2[1] + p1[1] * p3[0] + p2[0] * p3[1] -
        p2[1] * p3[0] - p1[1] * p2[0] - p1[0] * p3[1] >= 0;
    }