「HNOI2003」消防局的设立

题目

【内存限制：$256 MiB$】【时间限制：$1000 ms$】

【标准输入输出】【题目类型：传统】【评测方式：文本比较】

---

题目描述

2020 年，人类在火星上建立了一个庞大的基地群，总共有 $n$ 个基地。起初为了节约材料，人类只修建了 $n-1$ 条道路来连接这些基地，并且每两个基地都能够通过道路到达，所以所有的基地形成了一个巨大的树状结构。如果基地 $A$ 到基地 $B$ 至少要经过 $d$ 条道路的话，我们称基地 $A$ 到基地 $B$ 的距离为 $d$。

由于火星上非常干燥，经常引发火灾，人类决定在火星上修建若干个消防局。消防局只能修建在基地里，每个消防局有能力扑灭与它距离不超过 $2$ 的基地的火灾。

你的任务是计算至少要修建多少个消防局才能够确保火星上所有的基地在发生火灾时，消防队有能力及时扑灭火灾。

---

输入格式

输入文件的第一行为 $n$，表示火星上基地的数目。

接下来的 $n-1$ 行每行有一个正整数，其中文件第 $i$ 行的正整数为 $a_i$，表示从编号为 $i$ 的基地到编号为 $a_i$ 的基地之间有一条道路，为了更加简洁的描述树状结构的基地群，有 $a_i<i$。

---

输出格式

输出文件仅有一个正整数，表示至少要设立多少个消防局才有能力及时扑灭任何基地发生的火灾。

---

样例

样例输入

6
1
2
3
4
5

样例输出

2

---

数据范围与提示

$n\le 1000$

---

题解

做题经历

刚开始看，感觉这道题是一道较简单的树 $dp$ ，于是我想练练我贫穷的 $dp$ 技巧......结果花了差不多一个半小时得到了 $10pts$ ，然后在 $zxy$ 大佬的帮助下我当场 $AC$。

首先我的 $dp$ 定义：$dp[u][0|1]$：第 $u$ 个点建立/不建立消防站

于是我连 $dp$ 式都写不出来.....

---

正解

法Ⅰ：贪心的 $zxy$ 大佬

每访问到一个 $u$ 节点时，找一个二元组 $(minn,maxx)$ 表示在 $u$ 这棵子树中，建了消防站的点距离 $u$ 的距离最小值与在 $u$ 这棵子树上，还未被覆盖的点距离 $u$ 的距离最大值。

先贴一张图片，方便说明：

（这张图只是方便说明，可能与此题无关）

我们先来考虑这个二元组 $(minn,maxx)$ 。

首先我们需要保证的是，每个 $u$ 节点的儿子 $v$ ，对于以 $v$ 为根的子树都是已经被处理好的，即这个二元组 $(minn,maxx)$ 中的两个元素不能出现在同一棵子树中。

那么，这个已经被建立了消防站的点距离还未建立消防站的店的距离就是 $minn+maxx$。

假设我们访问到上图中的 $u=4$ 号节点，再假设距离其最近的且是其子树中的消防站是 $5$ ，而还未被覆盖的点是 $7$

那么可以计算数数得到 $minn=1,maxx=2$

那么节点 $5$ 与节点 $7$ 的距离就是 $dis=minn+maxx=1+2=3$

通过题目，我们知道一个消防站的染色范围是 $2$ ，也就是说如果这个 $dis≤2$ ，则说明这一整棵子树都已经被覆盖了（此处细想）

而如果 $dis>2$ ，则说明这个消防站无法覆盖完这棵树，那么就可能需要这个节点 $u$ 来建消防站来染色

为什么是可能呢？

我们来分析这样一种情况：$minn=4,maxx=1$

那么我们是不是必须在 $u$ 节点建消防站呢？

答案是不必须的，而且为了满足答案最优，我们还不能在此建立消防站。

为什么？

因为在 $maxx=1$ 时，说明如果我们在 $u$ 的父亲建立消防站，也是一样可以覆盖到这个尚未被覆盖的点。

而且可以保证，在 $u$ 的父亲建消防站是一定比在 $u$ 建消防站优的。

为什么？

还是同一张图：

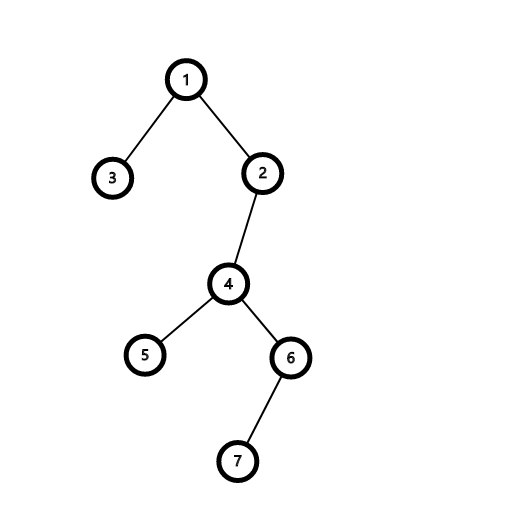
如果我们选择在节点 $4$ 建立消防站，而尚未被覆盖的点是 $6$ 。

想一想，在 $2$ 建立消防站是否一定比在 $4$ 更优？

我们来看一看，如果在 $4$ 建立消防站，可以覆盖的点就只有 $6、4$ 和 $2、1$（假设 $5、7$ 是已经被覆盖了的）

但是如果我们在 $2$ 建立消防站，可以覆盖的点就有 $3、1、2、4、6$

所以，在其他的节点都已被处理好的前提下，将消防站尽量往高处建是最优的。

但是什么时候不得不建呢？

那么就是当$maxx+minn>2且maxx=2$时，如果我们再往上回溯，那么 $maxx$ 是会大于 $2$ 的，就是说在其父亲节点建消防站时，是已经够不到那个离得最远的点的。

时间复杂度$O(能过)$，代码如下：

#include<bits/stdc++.h>
using namespace std;
template<class T>inline void qread(T& x){
    char c;bool f=false;x=0;
    while((c=getchar())<'0'||'9'<c)if(c=='-')f=true;
    for(x=(c^48);'0'<=(c=getchar())&&c<='9';x=(x<<1)+(x<<3)+(c^48));
    if(f)x=-x;
}
template<class T,class... Args>inline void qread(T& x,Args&... args){qread(x),qread(args...);}
inline int rqread(){
    char c;bool f=false;int x=0;
    while((c=getchar())<'0'||'9'<c)if(c=='-')f=true;
    for(x=(c^48);'0'<=(c=getchar())&&c<='9';x=(x<<1)+(x<<3)+(c^48));
    return f?-x:x;
}
template<class T>inline T Max(const T x,const T y){return x>y?x:y;}
template<class T>inline T Min(const T x,const T y){return x<y?x:y;}
template<class T>inline T fab(const T x){return x>0?x:-x;}
const int MAXN=1000;
const int INF=0x3f3f3f3f;
struct edge{
    int to,nxt;
    edge(){}
    edge(const int T,const int N):to(T),nxt(N){}
}e[(MAXN<<1)+5];
int tail[MAXN+5],edgeind;
inline void add_edge(const int u,const int v){
    e[++edgeind]=edge(v,tail[u]);tail[u]=edgeind;
    e[++edgeind]=edge(u,tail[v]);tail[v]=edgeind;
}
int N,dep[MAXN+5],tot;
struct node{
    int minn,maxx;
    node(){}
    node(const int N,const int X):minn(N),maxx(X){}
};//定义的二元组
void buildtre(const int u,const int pre){
    dep[u]=dep[pre]+1;
    for(int i=tail[u],v;i;i=e[i].nxt)if((v=e[i].to)!=pre)
        buildtre(v,u);
}
node dfs(const int u,const int pre){
    node t,ret=node(INF,0);
    for(int i=tail[u],v;i;i=e[i].nxt)if((v=e[i].to)!=pre){
        t=dfs(v,u);
        ret.minn=Min(ret.minn,t.minn);
        ret.maxx=Max(ret.maxx,t.maxx);
    }
    if(ret.minn+ret.maxx<=2)return node(ret.minn+1,0);
    if(ret.maxx==2)return ++tot,node(1,0);//除非不得不建，否则尽量往上走
    return node(ret.minn+1,ret.maxx+1);
}
signed main(){
    qread(N);
    for(int i=2;i<=N;++i)add_edge(i,rqread());
    buildtre(1,0);
    node t=dfs(1,0);
    if(t.maxx)++tot;//特殊处理根节点未覆盖的情况
    printf("%d\n",tot);
    return 0;
}

---

法Ⅱ：$lj$ 大佬的树 $dp$

我们分析这个消防站对于当前点的影响.

先来看这样一棵树：

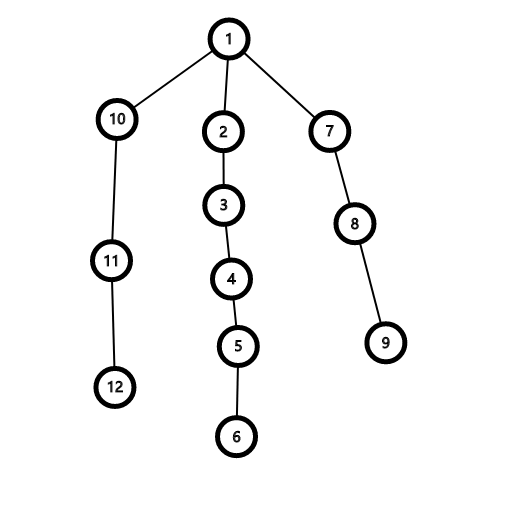
假设我们已经访问到节点 $1$。

我们先考虑在节点 $2$ 建立消防站，那么它可以覆盖到 $10、1、7$ 和 $3、4$

如果在节点 $3$ 建立消防站，可覆盖 $1、2、4、5$

不难发现，如果我们建立的消防站的深度不同，其覆盖的节点构成（我在前文用‘和’分开了不同的构成，自己区分）（区分节点）也是不同的

那么，这个 $dp$ 的定义是不是会和建立消防站的深度或者距离有关。

那么定义二维状态：

$dp[u][x]$：在节点 $u$ 的子树中，所建立的消防站离它的距离为 $x$ 时，所建立的最少的消防站。

那么又有一个问题，这个 $x$ 的取值为多少呢？

先将一棵树拆成一条单链来看

• 当 $x=0$ 时，毫无疑问，是在 $1$ 建立的消防站
• 当 $x=1$ 时，在 $2$ 建消防站，那么 $1、3、4$都是被覆盖的
• 当 $x=2$ 时，同上
• 当 $x=3$ 时，在 $4$ 建消防站。那么有一个问题，节点 $1$ 好像没有被覆盖？那么 $1$ 怎么覆盖呢？只有可能是其爷爷或者其父亲。
• 当 $x=4$ 时，在 $5$ 建消防站，同样有个问题， $1、2$ 没有被覆盖，那么就需要 $1$ 的父亲来覆盖了
• 当 $x=5$ 时，在 $6$ 建消防站。这下问题就变大了， $1、2、3$ 都没有被覆盖，无论是在爷爷还是父亲节点都无法覆盖 $3$ 了，这下就必须在 $1$ 建立节点（尽量将消防站建高）才能覆盖 $3$ ，那么与 $x=0$ 重复

我们发现，当 $x=5$ 时，状态已经重复，说明 $x$ 最大的取值就为 $5$。

现在开始考虑状转：

• 当 $x=0$ 时，$dp[u][0]=\sum dp[v][4]$
• 当 $x=1$ 时，$dp[u][1]=\sum dp[v][3]+min\{dp[v][0]-dp[v][3]\}$
• 当 $x=2$ 时，$dp[u][2]=\sum dp[v][1]$
• 当 $x=3$ 时，$dp[u][3]=\sum dp[v][2]$
• 当 $x=4$ 时，$dp[u][4]=\sum dp[v][3]$
• 当 $x=5$ 时，不用管 $dp[u][5]$，因为上面的状态已经不可能用到它了（仔细观察所调用到的 $dp[v][x]$ ，都没有发现 $dp[v][5]$ 的出现）

再加以修饰，又是一份 $AC$ 代码：摘自 $trymyedge(lj)$ 大佬：

#include <bits/stdc++.h>
#define mz 1000000007
using namespace std;

vector<int> vec[10005];
int dp[10005][5];

void dfs(int x, int fa) {
    dp[x][0] = 1;
    int minn = 9999;
    for (int i = 0; i < vec[x].size(); i++) {
        if (vec[x][i] != fa) {
            dfs(vec[x][i], x);
            dp[x][0] += dp[vec[x][i]][4];
            dp[x][1] += dp[vec[x][i]][3];
            minn = min(minn, dp[vec[x][i]][0] - dp[vec[x][i]][3]);
            dp[x][2] += dp[vec[x][i]][1];
            dp[x][3] += dp[vec[x][i]][2];
            dp[x][4] += dp[vec[x][i]][3];
        }
    }
    dp[x][1] += minn;
    if (dp[x][2] == 0)
        dp[x][2] = 9999;
    for (int i = 1; i <= 4; i++) dp[x][i] = min(dp[x][i - 1], dp[x][i]);
}

int main() {
    int n, x;
    scanf("%d", &n);
    for (int i = 2; i <= n; i++) {
        scanf("%d", &x);
        vec[x].push_back(i);
        vec[i].push_back(x);
    }
    dfs(1, 0);
    printf("%d\n", min(dp[1][0], min(dp[1][1], dp[1][2])));
    return 0;
}