简述树,Trie,Avl,红黑树

树的表示方法

　　在平时工作中通常有2种方式来表示树状结构，分别是孩子链表示法和父节点表示法。光说名词可能无法让人联系到实际场景中，但是写出代码之后大家一定就明白了。

　　孩子链表示法，即将树中的每个结点的孩子结点排列成一个线性表，用链表存储起来。对于含有 n 个结点的树来说，就会有 n 个单链表，将 n 个单链表的头指针存储在一个线性表中，这样的表示方法就是孩子表示法。

　　用代码展示即：

#define TElemType int
#define Tree_Size 100
//孩子表示法
typedef struct CTNode{
    int child;//链表中每个结点存储的不是数据本身，而是数据在数组中存储的位置下标
    struct CTNode * next;
}*ChildPtr;
typedef struct {
    TElemType data;//结点的数据类型
    ChildPtr firstchild;//孩子链表的头指针
}CTBox;
typedef struct{
    CTBox nodes[Tree_Size];//存储结点的数组
    int n,r;//结点数量和树根的位置
}CTree;

　　在存储方式上类似于

　　

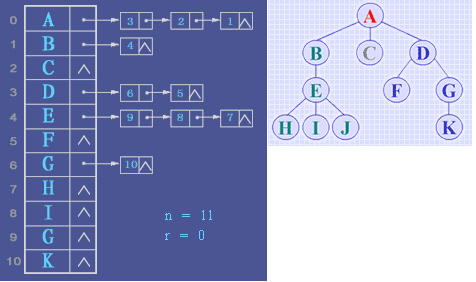
　　此种结构适合用于场景为：需要先出现父节点的场景，如：显示菜单，显示组织架构等。

　　父节点表示法，即取一块连续的内存空间，在存储每个结点的同时，各自都附加一个记录其父结点位置的变量。

　　用代码展示，即：

/* 树节点的定义 */
#define MAX_TREE_SIZE 100
typedef struct
{
  TElemType data;
  int parent; /* 父节点位置域 */
} PTNode;
typedef struct
{
  PTNode nodes[MAX_TREE_SIZE];
  int n; /* 节点数 */
} PTree;

　　在存储方式上类似于：

　　

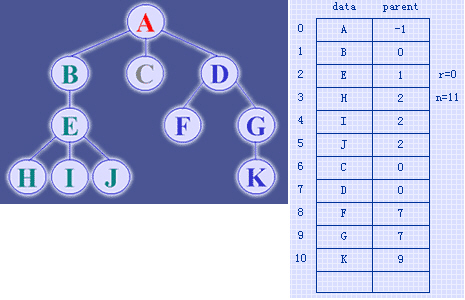
　　此结构适用于用在频繁查找父级节点的时候，如 溯源等。

　　在落地时，与写库相关用父级表示法，与读库相关用子级表示法，分库后用子级表示法。

简述线段树

　　定义：线段树是一个二叉树形状的数据结构，用于存储区间或者线段，并且允许快速查询结构内包含某一点的所有区间。

　　需要了解线段树，首先需要对前缀和，区间覆盖，区间加法，区间求和这几个概念有所了解。

　　简单来说，有这么两个线段，我要求7+8+9的时候只需要把上面这一条与下面这一条相减即可。

　　

　　当然上面这个比较简单，下面进行一点升级，如图：

　　

　　存储规则为第一项存第一项的值，第二项存前二项和，第三项存前三项和，以此类推。

　　这个时候当我要求7+8+9的时候 依然只需要将整条的值减去前6项和即可，即45-21。

　　简单白话来说即每一项内容都是一个集合，类似于上学期间学习的交并差集的感觉。

简述TRIE

　　TRIE,又称前缀树或字典树。是一种有序树，用于保存关联数组。详细定义参考维基百科定义，传送门

　　其形态类似于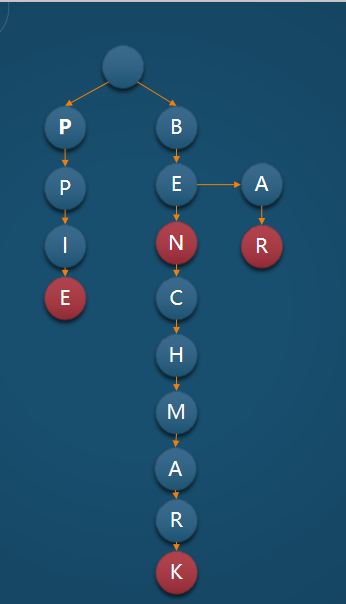 

　　比如说要将以下文字构造为Trie

　　add a count for the part-include for example

　　核心规则如图所示：

　　

　　文字版总结即：

　　1.添加一个空的root节点

　　2.从第一个单词第一个字母开始挨个排队从root穿过

　　3.当发现没有叫同一个字母的节点则开辟一条新的子节点

　　4.在单词最后一个字母的时候给节点打上标记，并记录次数

　　常用于词频分析，搜索提示等场景。

　　

简述AVL

　　定义：在计算机科学中，AVL树是最早被发明的自平衡二叉查找树。在AVL树中，任一节点对应的两棵子树的最大高度差为1，因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是{\displaystyle O(\log {n})}。增加和删除元素的操作则可能需要借由一次或多次树旋转，以实现树的重新平衡。

　　节点带有平衡因子0，1，-1的节点可以认为满足了AVL。平衡因子为：左边与右边子树的高度/深度差就是这个节点的平衡因子。

　　 

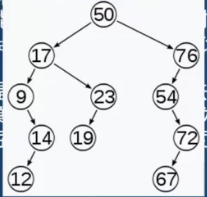
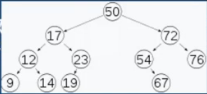
　　 如图所示，左边为非平衡树，右边为平衡树。

　　AVL平衡方式分为左旋和右旋。

　　左旋概念：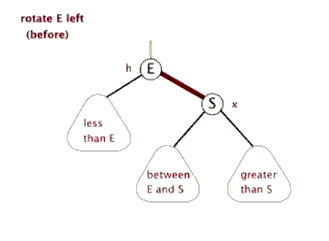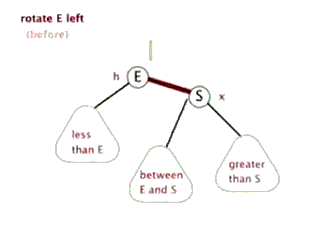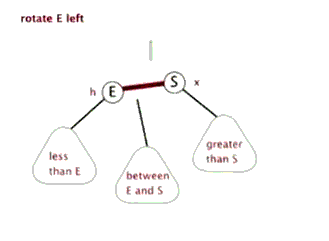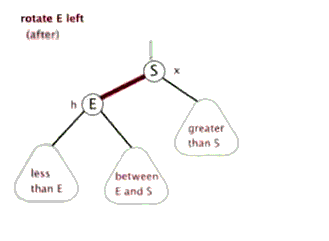

　　右旋概念：

　　简单理解就是向那边旋转就哪边的节点向下沉。

　　接下来稍微进阶一点点

　　

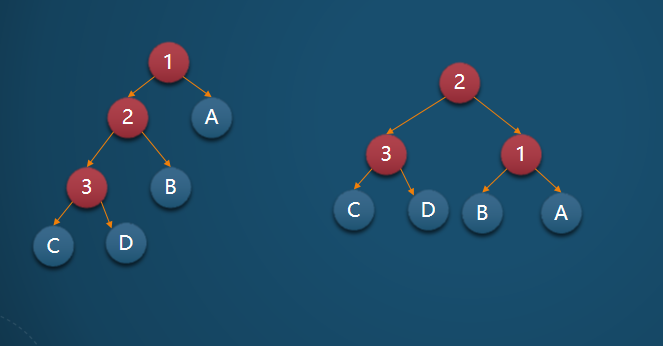
　　此为右旋 ，操作可以类比为将2拽起来 ，将1沉下去， 在过程中 2与b的结构发生断裂 b变成了单身狗正好看见了A于是b为了脱单于是和1连上了。

　　同样的还有左旋如下图所示。

　　

　　

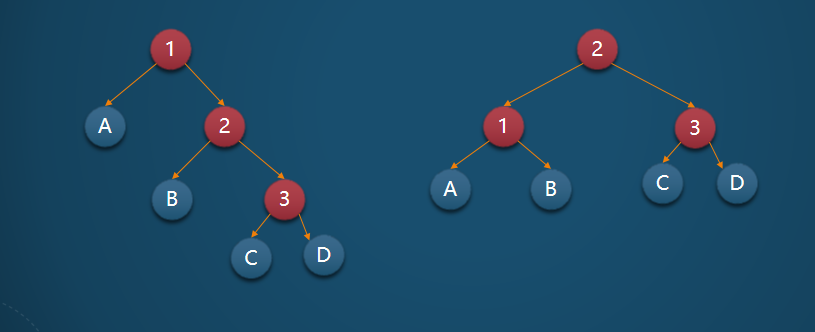
简述红黑树

　　红黑树（英语：Red–black tree）是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。维基百科传送门

　　规则如下：

　　1.节点是红色或者黑色.

　　2.根是黑色.

　　3.所有的叶子都是黑色

　　4.每个红色节点必须有两个黑色的子节点(其实就是3的一个推演)

　　5.从任意一个节点到每个叶子的所有简单路径都包含相同数目的黑色节点.(这一条涉及了图论..嗯..你简单认为就是,除了起点跟终点没有重复定点的道路就叫做简单道路)

　　6.每个叶子节点到根的我所有路径上不能有两个连续的红色节点

　　如图：

　　

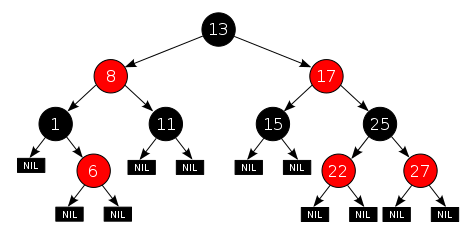
　　适合进行统计时使用。

落地举例

　　假定123456对应为月份的消费金额，节点上每一个代表下标区间

　　

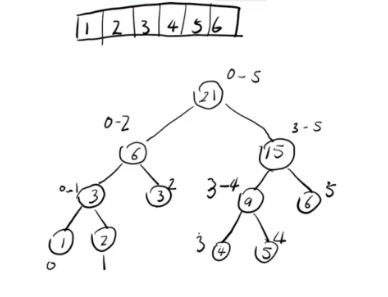
　　则可以很容易的统计出 这个用户在0-1月份消费了多少钱 ，3-5月份消费了多少钱等，应用线段树的概念可以很方便的统计出想统计的范围的结果。

　　如果使用红黑树的结构 则黑色的叶子节点可以认为是原始数据，红色节点可以认为是统计数据。