线性代数 -- Linear Algebra with Applications

@、如果线性方程组无解，则称该方程组是不相容的（inconsistent）。

@、如果线性方程组至少存在一个解，则称该方程组是相容的（consistent）。

@、等价方程组（equivalent systems）。

@、定义：若两个含有相同变量的方程组具有相同的解集，则称它们是等价的（equivalent）。

@、得到等价的方程组：

1、交换任意两个方程的顺序。

2、任一方程两边同乘一个非零的实数。

3、任一方程的倍数加到另一方程上。

@、定义：若方程组中，第k个方程的前k-1个变量的系数均为零，且x_k(k=1, ..., n)的系数不为零，则称该方程组为严格三角形的（strict triangular form）。

@、求解严格三角形方程组的方法：回代（back substitution）。

@、方程组的系数矩阵（coefficient matrix）。

@、方程组的增广矩阵（augmented matrix）。

@、初等行运算：

1、交换两个。

2、以非零实数乘以某行。

3、将某行替换为它与其他行的倍数的和。

@、主行（pivotal row）：用来消去其他行元素。

@、主元（pivot）：主行的第一个非零元素。

@、首变量（lead variables）：化简后增广矩阵每一行第一个非零元对应的变量。

@、自由变量（free variables）：化简过程中跳过的列对应的变量（即除了首变量的变量）。

@、定义：若一个矩阵满足

1、每一非零行中的第一个非零元为1；

2、第k行的元不全为零时，第k+1行首变量之前的零的个数多于第k行首变量之前零的个数；

3、所有元素均为零的行必在不全为零的行之后。

则称为行阶梯形矩阵（row echelon form）。

@、高斯消元法（Gaussian elimination）：定义： 利用行运算1、2和3，将线性方程组的增广矩阵化为行阶梯形的过程称为高斯消元法。

@、超定方程组：若一个线性方程组中方程的个数多于未知量的个数，则称其为超定的（overdetermined）。超定方程组通常是（但不总是）不相容的。

@、亚定方程组：若一个线性方程组中方程的个数(n)多于未知量的个数(m)，则称其为亚定的（underdetermined）。亚定方程组有可能不相容，但通常是相容的，其有无穷多个解。因为行阶梯形式均有r（r<=m）个首变量，那么必有n-r（n-r>=n-m>0）个自由变量，当自由变量取不同值时，可得到不同的解。

@、定义 若一个矩阵满足

1、 矩阵是行阶梯形的；

2、每一行的第一个非零元是该列惟一的非零元，

则称该矩阵为行最简形（reduced row echelon form）。

@、高斯 - 若尔当消元法（Gauss-Jordan reduction）：采用基本行运算将矩阵化为行最简形的过程。

@、齐次方程组：如果线性方程组的右端项全为零，则称其为齐次的（homogeneous）。齐次方程组总是相容的，至少有一个平凡解。

@、平凡解：(0, 0, ..., 0)。即所有变量的值都为零。

@、非平凡解：不是(0, 0, ..., 0)的解。

@、定理1.2.1 若n>m，则m * n的齐次线性方程组有非平凡解。

@、矩阵中的元素称为标量（scalar）。通常是实数或复数。

@、一般若用A表示矩阵，则a_ij表示矩阵A的第i行第j列的元素。矩阵简记为：A = (a_ij)。

@、向量（vector）：由实数组成的n元组。

@、行向量（row vector）：用一个1*n的矩阵来表示n元组。

@、列向量（column vector）：用一个n*1的矩阵来表示n元组。

@、在使用矩阵方程时，用列向量表示解较为方便，所以n*1的实矩阵构成的几何称为n维欧几里得空间（Euclidean n-space），通常记为Rⁿ。

@、定义 若两个m*n矩阵A和B对任一i和j均满足a_ij = b_ij，则称它们相等（equal）。

@、标量乘法：定义：设A为m*n的矩阵，且α为一标量，则αA为一m*n的矩阵，其(i, j)元素为αa_ij。

@、矩阵加法：定义：设A=(a_ij)及B=(b_ij)都是m*n矩阵，则它们的和(sum)A+B也为一个m*n的矩阵，对每一个有序对(i, j)，它的(i, j)元素为a_ij + b_ij。

@、零矩阵（zero matirx）：元素全为零的矩阵。用O表示。

@、A与O都是m*n的矩阵，O是零矩阵，则：

1、A + O = O + A = A；

2、A + (-1)A = O = (-1)A + A;

@、定义 若a₁, a₂, ..., a_n 为R^m中的向量，且c₁, c₂, ..., c_n为标量，则和式 c₁a₁ + c₂a₂ + ... + c_na_n 称为向量 a₁, a₂, ..., a_n 的一个线性组合（linear combination）。

@、定理1.3.1（线性方程组的相容性定理） 一个线性方程组 Ax = b 相容的充要条件是向量 b 可写为矩阵 A 列向量的一个线性组合。

@、定义 若 A=(a_ij)为一个 m*n 的矩阵，且B=(b_ij)为一个 n*r 的矩阵，则乘积AB=C=(c_ij)为一个 m*r 的矩阵，它的元素定义为：c_ij = a^→_ib_j = ∑a_ikb_kj
。（注：a^→_i表示矩阵A的第i个行向量）

@、矩阵乘法不满足交换率，即 AB != BA。

@、定义 一个 m*n 矩阵A的转置（transpose）为 n*m 矩阵B，定义为 b_ji = a_ij 其中j=1, ..., n 和 i=1, ..., m. A的转置记为A^T。

@、定义 一个 n*n 的矩阵A， 若满足A^T=A，则称为对称的（symmetric）。

@、矩阵代数的法则：

@、单位矩阵（identity matrix）: I = (δ_ij)，其中δ_ij = 1（当 i = j）或者 0 （当 i ≠ j）。 BI = B， IC = C。

@、使用列向量表示I， I = (e₁, e₂, ..., e_n)，不使用 i_j。

@、定义 若存在一个矩阵B使得AB=BA=I，则称 n*n 矩阵A为非奇异的（nonsingular）或可逆的（invertible）。矩阵B称为A的乘法逆元（multiplication inverse）。

@、若B和C均为A的乘法逆元，则 B = BI = B(AC) = (BA)C = IC = C，因此，一个矩阵最多有一个乘法逆元。A的逆元记作A^-1。

@、定义 一个 n*n 矩阵若不存在乘法逆元，则称为奇异的（singular）。

@、只有方阵(即矩阵行数等于列数)有乘法逆元。对于非方阵，不应使用术语奇异或非奇异。

@、定理1.4.2 若A和B为非奇异的n*n矩阵，则AB也为非奇异的，且(AB)^-1 = B^-1A^-1。

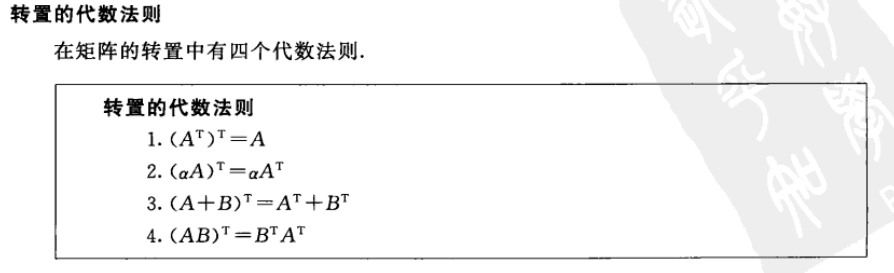
@、转置的代数法则：

@、定理1.4.3 设A为某图的n*n邻接矩阵，且a^(k)_ij表示A^k的(i, j)元素，则a^(k)_ji等于顶点V_i和V_j间长度为k的路的条数。