深入理解KMP算法之续篇

前言：

纠结于KMP已经两天了，相较于本人之前博客中提到的几篇博文，本人感觉这篇文章更清楚地说明了KMP算法的来龙去脉。

http://www.cnblogs.com/goagent/archive/2013/05/16/3068442.html

1、传统的字符串匹配算法

/*
 * 从s中第sIndex位置开始匹配p
 * 若匹配成功，返回s中模式串p的起始index
 * 若匹配失败，返回-1
 */
int index(const std::string &s, const std::string &p, const int sIndex = 0)
{
    int i = sIndex, j = 0;

    if (s.length() < 1 || p.length() < 1 || sIndex < 0)
    {
        return -1;
    }

    while (i != s.length() && j != p.length())
    {
        if (s[i] == p[j])
        {
            ++i;
            ++j;
        }
        else
        {
            i = i - j + 1;
            j = 0;
        }
    }
    return j == p.length() ? i - j: -1;
}

2、传统字符串匹配算法的性能问题

用模式串P去匹配字符串S，在i=6,j=4时发生失配：

i=6

S: a   b   a   b   c   a   d   c   a   c   b   a   b

P:           a   b   c   a   c

j=4

此时，按照传统算法，应当将P的第 1 个字符 a(j=0) 滑动到与S中第4个字符 b(i=3) 对齐再进行匹配：

i=3

S: a   b   a   b   c   a   a   d   a   c   b   a   b

P:               a   b   c   a   c

j=0

这个过程中，对字符串S的访问发生了“回朔”（从 i=6 移回到 i=3）。

我们不希望发生这样的回朔，而是试图通过尽可能的“向右滑动”模式串P，让P中index为 j 的字符对齐到S中 i=5 的字符，然后试图匹配S中 i=6 的字符与P中index为 j+1 的字符。

在这个测试用例中，我们直接将P向右滑动3个字符，使S中 i=5 的字符与P中 j=0 的字符对齐，再匹配S中 i=6 的字符与P中 j=1 的字符。

i=6

S: a   b   a   b   c   a   d   c   a   c   b   a   b

P:                        a   b   c   a   c

j=0

3、kmp算法的一般性讨论

下面讨论在一般性的情况下，如何实现在“不回朔”访问S、仅依靠“滑动”P的前提下实现字符串匹配，即“kmp算法”。

i=6

S: a   b   a   b   c   a   d   c   a   c   b   a   b

P:                        a   b   c   a   c

k=1

i=6

S: a   b   a   b   c   a   d   c   a   c   b   a   b

P:           a   b   c   a   c

j=4

对于任意的S和P，当S中index为 i 的字符和P中index为 j 的字符失配时，我们假定应当滑动P使其index为 k 的字符与S中index为 i 的字符“对齐”并继续比较。

那么，这个 k 是多少？

我们知道，所谓的对齐，就是要让S和P满足以下条件（上图中的蓝色字符）：

……（1）

另一方面，在失配时我们已经有了一些部分匹配结果（上图中的绿色字符）：

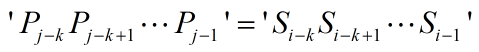……（2）

由（1）、（2）可以得到：

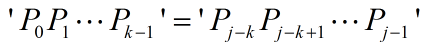……（3）

即如下图所示效果：

定义next[j]=k，k表示当模式串P中index为 j 的字符与主串S中index为 i 的字符发生失配时，应将P中index为 k 的字符继续与主串S中index为 i 的字符比较。

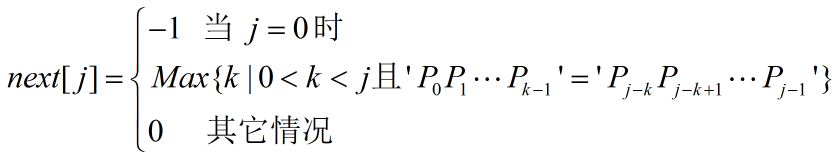……（4）

按上述定义给出next数组的一个例子：

j         0  1  2  3  4  5  6  7

P        a   b  a  a  b  c  a   c

next[j]  -1  0  0  1  1  2  0  1

在已知next数组的前提下，字符串匹配的步骤如下：

i 和 j 分别表示在主串S和模式串P中当前正待比较的字符的index，i 的初始值为sIndex，j 的初始值为0。

在匹配过程中的每一次循环，若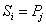，i 和 j 分别增 1，

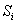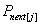else，j 退回到 next[j]的位置，此时下一次循环是与相比较。

4、kmp算法的实现

在已知next函数的前提下，根据上面的步骤，kmp算法的实现如下：

int kmp(const std::string& s, const std::string& p, const int sIndex = 0)
{
    std::vector<int>next(p.size());
    getNext(p, next);//获取next数组，保存到vector中

    int i = sIndex, j = 0;
    while(i != s.length() && j != p.length())
    {
        if (j == -1 || s[i] == p[j])
        {
            ++i;
            ++j;
        }
        else
        {
            j = next[j];
        }
    }

    return j == p.length() ? i - j: -1;
}

ok，下面的问题是怎么求模式串 P 的next数组。

next数组的初始条件是next[0] = -1，设next[j] = k，则有：

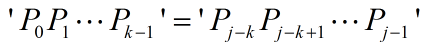
那么，next[j+1]有两种情况：

①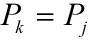，则有：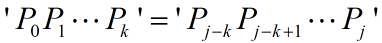

此时next[j+1] = next[j] + 1 = k + 1

②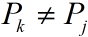， 如图所示：

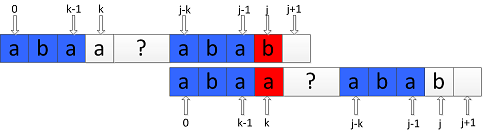
此时需要将P向右滑动之后继续比较P中index为 j 的字符与index为 next[k] 的字符：

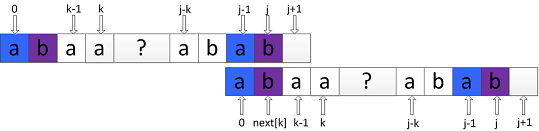
值得注意的是，上面的“向右滑动”本身就是一个kmp在失配情况下的滑动过程，将这个过程看 P 的自我匹配，则有：

如果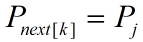，则next[j+1] = next[k] + 1；

否则，继续将 P 向右滑动，直至匹配成功，或者不存在这样的匹配，此时next[j+1] = 0。

getNext函数的实现如下：

void getNext(const std::string &p, std::vector<int> &next)
{
    next.resize(p.size());
    next[0] = -1;

    int i = 0, j = -1;

    while (i != p.size() - 1)
    {
        //这里注意，i==0的时候实际上求的是next[1]的值，以此类推
        if (j == -1 || p[i] == p[j])
        {
            ++i;
            ++j;
            next[i] = j;
        }
        else
        {
            j = next[j];
        }
    }
}

至此，一个完整的kmp已经实现。

5、getNext函数的进一步优化

注意到，上面的getNext函数还存在可以优化的地方，比如：

i=3

S: a   a   a   b   a   a   a   a   b

P: a   a   a   a   b

j=3

此时，i=3、j=3时发生失配，next[3]=2，此时还需要进行 3 次比较：

i=3, j=2;

i=3, j=1;

i=3, j=0。

而实际上，因为i=3, j=3时就已经知道a!=b，而之后的三次依旧是拿 a 和 b 比较，因此这三次比较都是多余的。

此时应当直接将P向右滑动4个字符，进行 i=4， j=0的比较。

一般而言，在getNext函数中，next[i]=j，也就是说当p[i]与S中某个字符匹配失败的时候，用p[j]继续与S中的这个字符比较。

如果p[i]==p[j]，那么这次比较是多余的（如同上面的例子），此时应该直接使next[i]=next[j]。

完整的实现代码如下：

void getNextUpdate(const std::string& p, std::vector<int>& next)
{
    next.resize(p.size());
    next[0] = -1;

    int i = 0, j = -1;

    while (i != p.size() - 1)
    {
        //这里注意，i==0的时候实际上求的是nextVector[1]的值，以此类推
        if (j == -1 || p[i] == p[j])
        {
            ++i;
            ++j;
            //update
            //next[i] = j;
            //注意这里是++i和++j之后的p[i]、p[j]
            next[i] = p[i] != p[j] ? j : next[j];
        }
        else
        {
            j = next[j];
        }
    }
}

对应的，只需要在kmp算法中将 getNext(p, next); 替换成 getNextUpdate(p, next); 即可。

6、时间复杂度分析

下面以getNext函数为例，分析kmp算法的时间复杂度。

 1 void getNext(const std::string& p, std::vector<int>& next)
 2 {
 3     next.resize(p.size());
 4     next[0] = -1;
 5
 6     int i = 0, j = -1;
 7
 8     while (i != p.size() - 1)
 9     {
10         if (j == -1 || p[i] == p[j])
11         {
12             ++i;
13             ++j;
14             next[i] = j;
15         }
16         else
17         {
18             j = next[j];
19         }
20     }
21 }

假定p.size()为m，分析其时间复杂度的困惑在于，在while里面不是每次循环都执行 ++i 操作，所以整个while的执行次数不一定为m。

换个角度，注意到在每次循环中，无论 if 还是 else 都会修改 j 的值且每次循环仅对 j 进行一次修改，所以在整个while中 j 被修改的次数即为getNext函数的时间复杂度。

每次成功匹配时，++i; ++j; , 由于 ++i 最多执行 m-1 次，故++j也最多执行 m-1 次，即 j 最多增加m-1次；

对应的，只有在 j=next[j]; 处 j 的值一定会变小，由于 j 最多增加m-1次，故 j 最多减小m-1次。

综上所述，getNext函数的时间复杂度为O(m)，若带匹配串S的长度为n，则kmp函数的时间负责度为O(m+n)。

7、kmp的应用优势

①快，O(m+n)的线性最坏时间复杂度；

②无需回朔访问待匹配字符串S，所以对处理从外设输入的庞大文件很有效，可以边读入边匹配。