洛谷P1140 相似基因（线性DP)

题目背景

大家都知道，基因可以看作一个碱基对序列。它包含了444种核苷酸，简记作A,C,G,TA,C,G,TA,C,G,T。生物学家正致力于寻找人类基因的功能，以利用于诊断疾病和发明药物。

在一个人类基因工作组的任务中，生物学家研究的是：两个基因的相似程度。因为这个研究对疾病的治疗有着非同寻常的作用。

题目描述

两个基因的相似度的计算方法如下：

对于两个已知基因，例如AGTGATGAGTGATGAGTGATG和GTTAGGTTAGGTTAG，将它们的碱基互相对应。当然，中间可以加入一些空碱基-，例如：

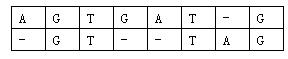
这样,两个基因之间的相似度就可以用碱基之间相似度的总和来描述，碱基之间的相似度如下表所示：

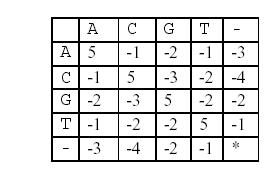
那么相似度就是：(−3)+5+5+(−2)+(−3)+5+(−3)+5=9(-3)+5+5+(-2)+(-3)+5+(-3)+5=9(−3)+5+5+(−2)+(−3)+5+(−3)+5=9。因为两个基因的对应方法不唯一，例如又有：

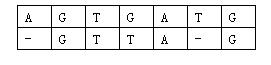
相似度为：(−3)+5+5+(−2)+5+(−1)+5=14(-3)+5+5+(-2)+5+(-1)+5=14(−3)+5+5+(−2)+5+(−1)+5=14。规定两个基因的相似度为所有对应方法中，相似度最大的那个。

输入格式

共两行。每行首先是一个整数，表示基因的长度；隔一个空格后是一个基因序列，序列中只含A,C,G,TA,C,G,TA,C,G,T四个字母。1≤1 \le 1≤序列的长度≤100 \le 100≤100。

输出格式

仅一行，即输入基因的相似度。

输入输出样例

输入 #1

7 AGTGATG
5 GTTAG

输出 #1

14
首先放上一篇超棒的题解：https://www.luogu.com.cn/paste/u7l8dqnn
这是一道线性DP题，蓝书上说得好，如果一个动态规划的算法包含多个维度，但在每个维度上都具有线性变化的阶段，这同样称为线性DP。这道题一看有两个字符串，联想到另一道题“编辑距离”，可以想到要开一个二维数组来存储，即dp[i][j]表示a串的1到i个碱基与b串的1到j个碱基的相似度。状态找到后开始写转移方程。由题意得，不考虑边界的话一共有三种情况，即dp[i][j]可能等于：
1.dp[i-1][j-1]+rela(a[i],b[j]).这表示a[i]与b[j]两个碱基彼此配对，其中rela(p,q)表示碱基p和碱基q的相似度。
2.dp[i-1][j]+rela(a[i],' ').这表示a[i]与空碱基配对。这里要注意到动态规划里无后效性的概念，不用去管a的前i-1个碱基与b的前j个碱基如何配对，只需要分析眼前情况。
3.dp[i][j-1]+rela(b[j],' ').这表示b[j]与空碱基配对。
最终要在这三者中取最大就得到转移方程。输出的答案存在dp[lena][lenb]中。lena，lenb分别表示a，b串的长度。

#include <bits/stdc++.h>
using namespace std;
char a[],b[];
int lena,lenb;
int dp[][]={-}; //dp[i][j]表示a的第i个与b的第j个到之前的相似度
map<char,int>m;
int pos=;
int rela[][]=//二维数组存储碱基与碱基之间的相似度
{
    {,-,-,-,-},
    {-,,-,-,-},
    {-,-,,-,-},
    {-,-,-,,-},
    {-,-,-,-,}
};
int mmax(int a,int b,int c)
{
    return max(max(a,b),c);
}
int main()
{
    scanf("%d%s",&lena,a);
    scanf("%d%s",&lenb,b);
    int i,j;
    m['A']=;//字典映射碱基到对应的下标，方便获得相似度
    m['C']=;
    m['G']=;
    m['T']=;
    m[' ']=;
    dp[][]=;
    for(i=;i<=lena;i++)//边界只有一种情况
    {
        dp[i][]=dp[i-][]+rela[m[a[i-]]][];
    }
    for(j=;j<=lenb;j++)
    {
        dp[][j]=dp[][j-]+rela[][m[b[j-]]];
    }
    for(i=;i<=lena;i++)
    {
        for(j=;j<=lenb;j++)
        {
            if(i&&j)
            {
                dp[i][j]=mmax(//手写的三个数取最大的mmax函数
                dp[i-][j-]+rela[m[a[i-]]][m[b[j-]]],
                dp[i-][j]+rela[m[a[i-]]][],
                dp[i][j-]+rela[][m[b[j-]]]
                        );
            }
        }
    }
    cout<<dp[lena][lenb];//输出答案。这里注意不要习惯性的写成dp[lena-1][lenb-1]，再次回顾dp[i][j]的定义，是“第i个”
    return ;
 }