md详解和rd详解：一次性创建多个目录和多级子目录

md 命令：

官方解释：

E:\ABC>md /?

创建目录。

MKDIR [drive:]path

MD [drive:]path

如果命令扩展被启用，MKDIR 会如下改变:

如果需要，MKDIR 会在路径中创建中级目录。例如: 假设 \a 不

存在，那么:

mkdir \a\b\c\d

与:

mkdir \a

chdir \a

mkdir b

chdir b

mkdir c

chdir c

mkdir d

相同。如果扩展被停用，则需要键入 mkdir \a\b\c\d。

E:\ABC>

rd命令

官方解释：

E:\ABC>rd /?

删除一个目录。

RMDIR [/S] [/Q] [drive:]path

RD [/S] [/Q] [drive:]path

/S      除目录本身外，还将删除指定目录下的所有子目录和

文件。用于删除目录树。

/Q      安静模式，带 /S 删除目录树时不要求确认

E:\ABC>

一、一次性建立多级子目录

输入命令“md r1\r2\r3”，创建一个多级子目录r1\r2\r3

例如：E:\ABC\Data\Y2018\M01\D01

cd E:\ABC\Data\Y2018\M01\D01

md r1\r2\r3

效果如下：

E:\ABC\Data\Y2018\M01\D01\r1\r2\r3

二、一次创建多个目录

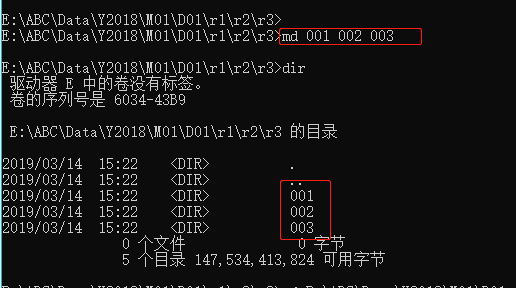
输入命令“md 001 002 003”,创建001 002 003目录，001 002 003属于同一级目录

例如：E:\ABC\Data\Y2018\M01\D01\r1\r2\r3

cd E:\ABC\Data\Y2018\M01\D01\r1\r2\r3

md 001 002 003

效果如下：

E:\ABC\Data\Y2018\M01\D01\r1\r2\r3\001

E:\ABC\Data\Y2018\M01\D01\r1\r2\r3\002

E:\ABC\Data\Y2018\M01\D01\r1\r2\r3003

三、rd删除目录

例如：删除r1\r2\r3 多级目录

cd E:\ABC\Data\Y2018\M01\D01

1.删除r1\r2\r3 多级目录

rd /s .\r1

或者rd /s .\r1\r2\r3

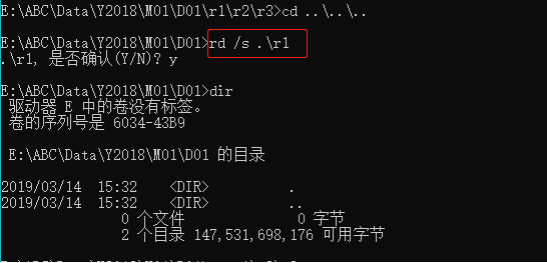
2.不使用/s 是删除不了多级目录的，提示r2目录不为空

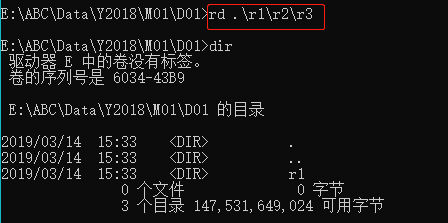
3.rd .\r1\r2\r3 仅仅删除了r3目录，r2和r1依然存在

附语：当然也可以使用xcopy命令来创建多级子目录

复制text.txt文件到E:\ABC\Data\Y2018\M01\D01\rzl20180101目录下，假如Y2018\M01\D01\rzl20180101\这些目录之前没有，使用以下命令后也会自动创建
xcopy /Q /Y E:\test.txt E:\ABC\Data\Y2018\M01\D01\rzl20180101\
xcopy /Q /Y E:\test.txt E:\ABC\Data\Y2018\M01\D02\rzl20180102\
xcopy /Q /Y E:\test.txt E:\ABC\Data\Y2018\M01\D03\rzl20180103\
xcopy /Q /Y E:\test.txt E:\ABC\Data\Y2018\M01\D04\rzl20180104\
xcopy /Q /Y E:\test.txt E:\ABC\Data\Y2018\M01\D05\rzl20180105\

效果如下：

E:\ABC\Data\Y2018\M01\D01\rzl20180101\test.txt

E:\ABC\Data\Y2018\M01\D02\rzl20180102\test.txt

 rzl_20190314记录