objectarx 多段线自交检查

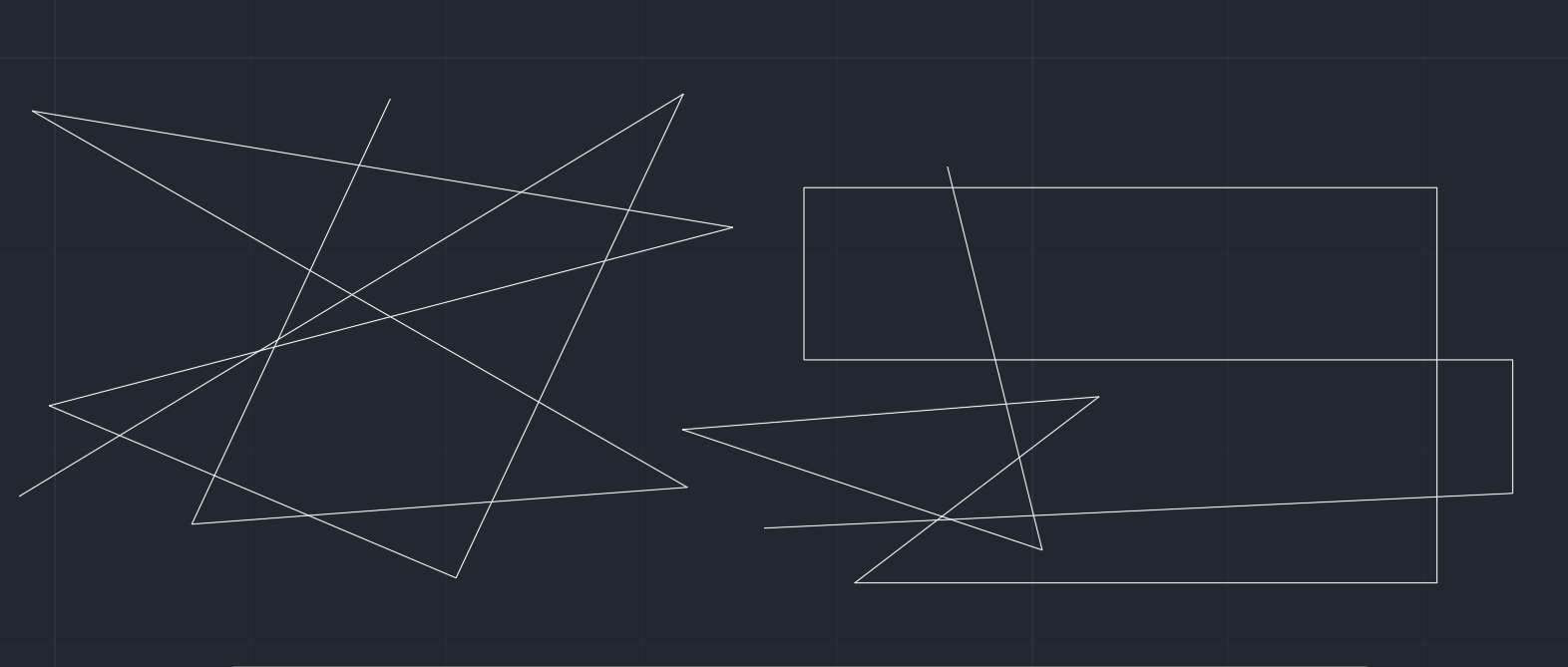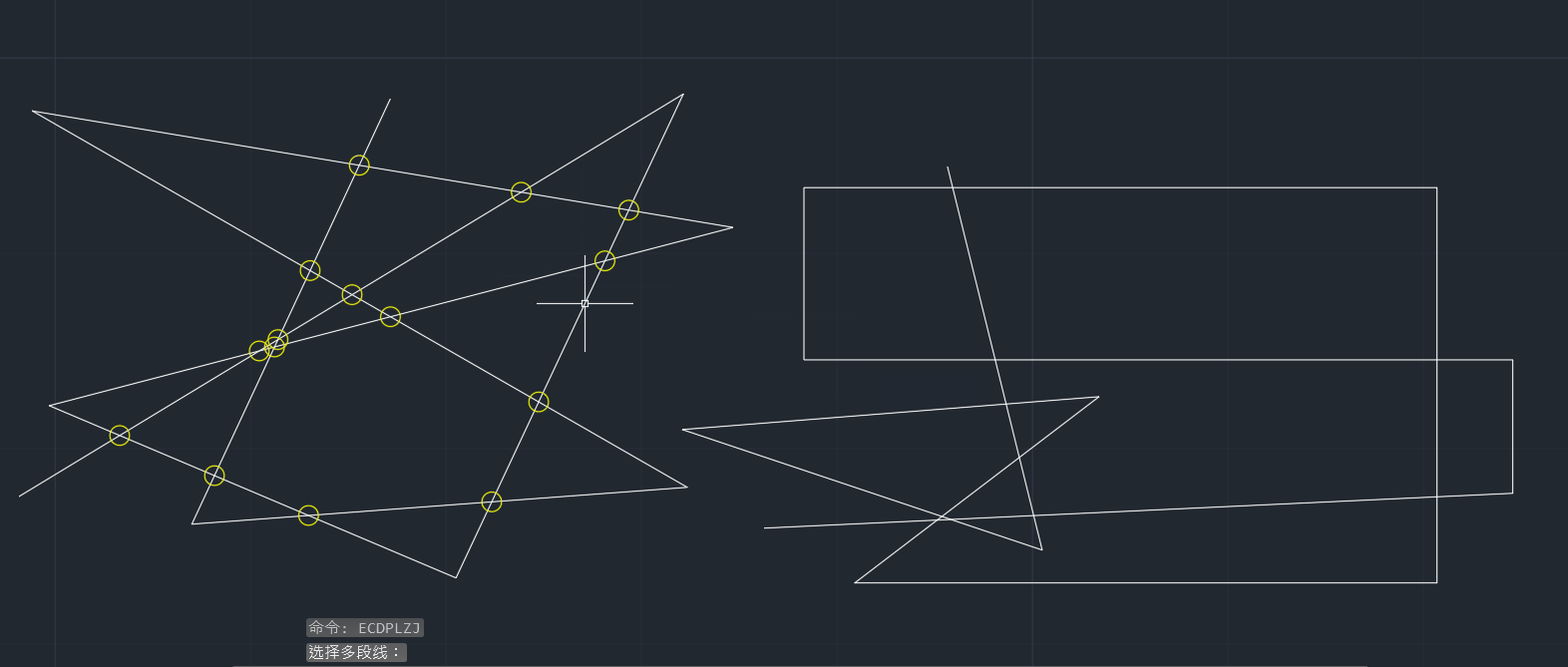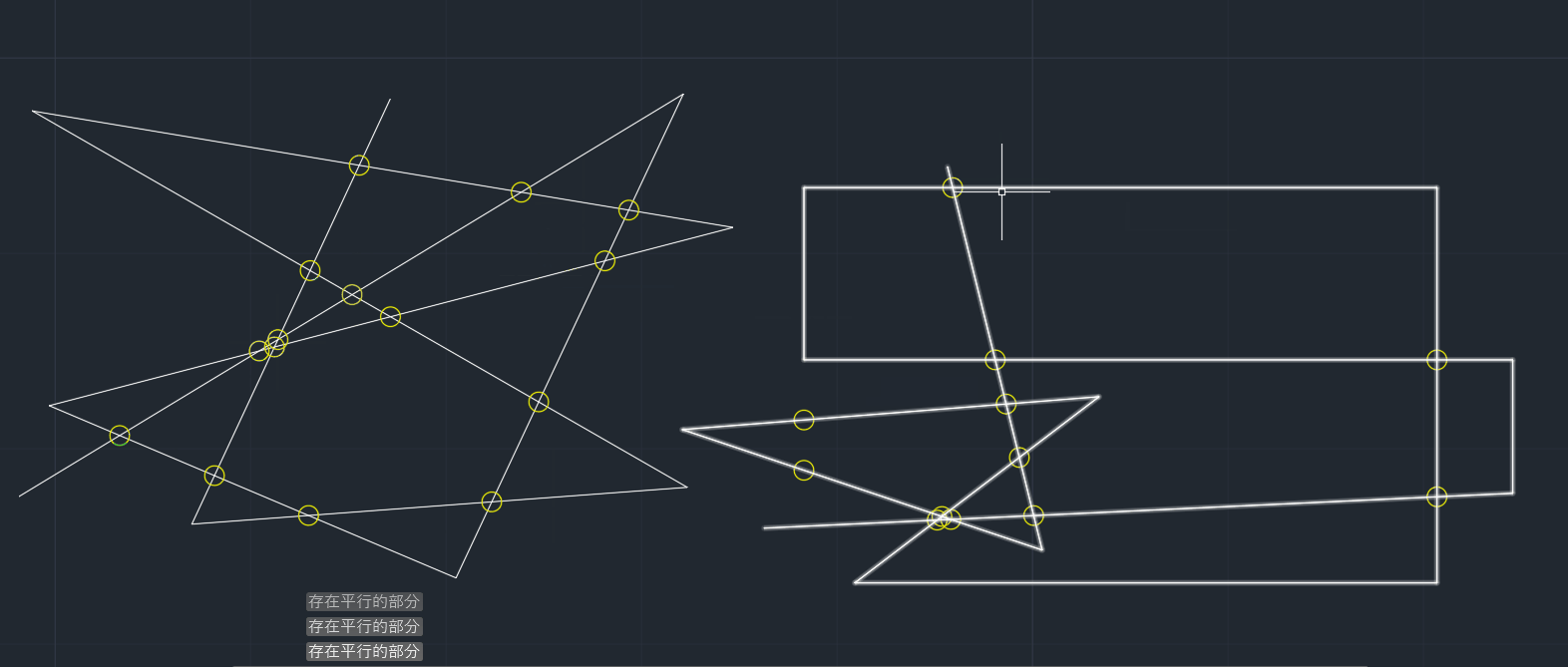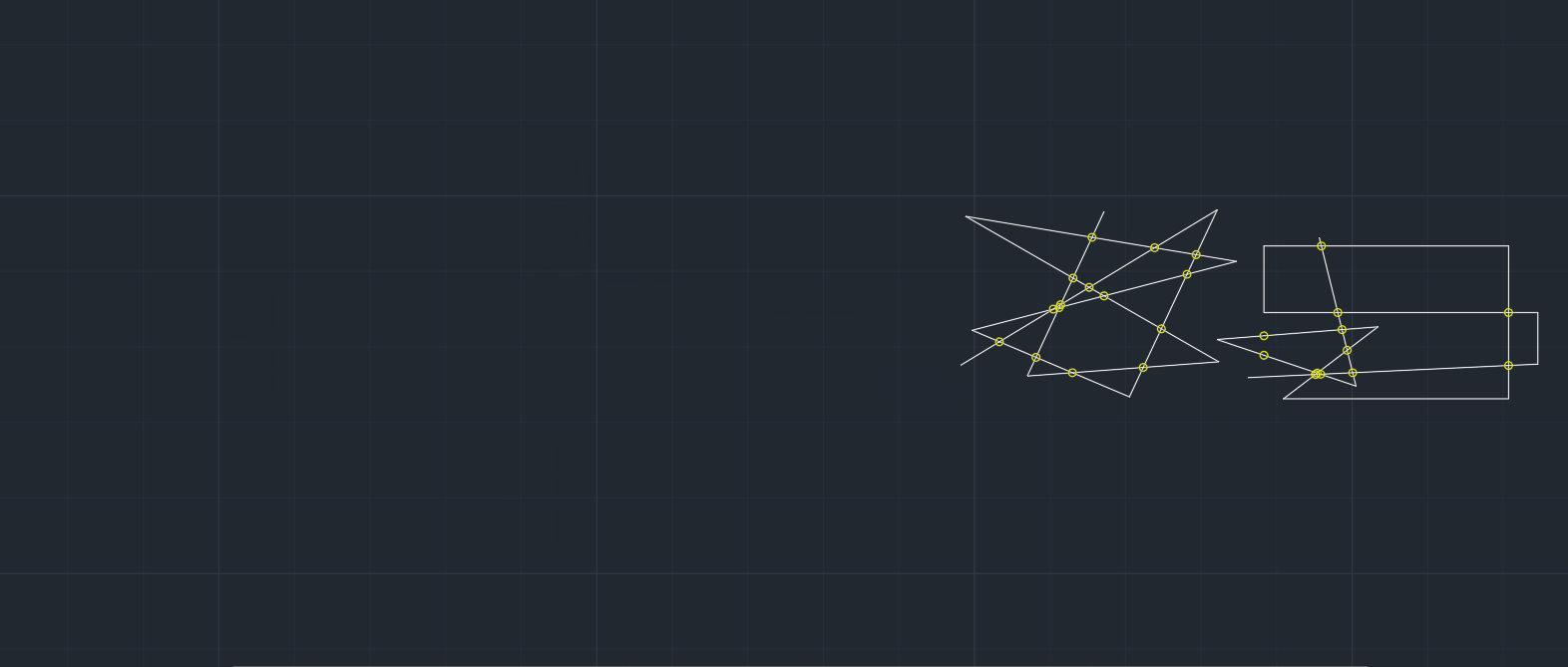
只支持直线段的多段线检查，因为主要用了初中的知识，一元一次方程求交点，详细的说就是，把多段线上相邻的两个点构成一条直线段，然后每条直线段与剩余的直线段求交点，一条直线段就代表一个一元一次方程，知道两点就知道这个方程是什么样的。
求出交点之后得判断这个点是否是多段线上本身的点，判断方法是判断求出来的交点与构成交点的两条直线段的4个点做比较，如果点的误差在1e-4之内，就认为这个交点是在多段线的端点上，不作为要求的交点。
除了这种可能之外，所求交点有可能是在直线段的延长线上，通过观察可以知道，如果交点在任意一条直线段两个端点之间，则可以知道这个交点到这条直线段两个端点的距离都要小于这个直线段两个端点的距离，如果交点到两个端点的距离大于了两个端点的距离，则说明这个交点是在线段的延长线上，也不作为要求的交点。
还需要注意的地方是，要考虑直线段垂直于x轴的情况，因为要求直线方程时的斜率时，分母不能为0，需要把直线垂直于x轴的情况单独考虑。

除了这种思路外，还可以直接使用intersectwith函数来做，相交类型是都不延长，（不知是直接炸开这个多段线好，还是分割这个多段线好）。总之首先得得到两个端点之间的线段。这样作，不仅支持直线段的多段线，还支持带凸度的，带圆弧的多段线了。
下面放出使用到的函数：

static    bool IsEqual(const AcGePoint2d & firstPoint, const AcGePoint2d & secondPoint, double tol)
    {
        return (fabs(firstPoint.x - secondPoint.x) < tol&&
            fabs(firstPoint.y - secondPoint.y) < tol);
    }

struct StLine
{
	AcGePoint2d ptPre;

	AcGePoint2d ptNext;

};

static bool JiaoDian(StLine &l1, StLine &l2, AcGePoint3d& ptCenter) {

        double x0, y0, x1, y1, x2, y2, x3, y3;

        x0 = l1.ptPre.x;
        y0 = l1.ptPre.y;

        x1 = l1.ptNext.x;
        y1 = l1.ptNext.y;

        x2= l2.ptPre.x;
        y2 = l2.ptPre.y;

        x3 = l2.ptNext.x;
        y3 = l2.ptNext.y;

        if (x0 - x1 == ) {
            if (x2 - x3 == )
            {
                if (IsEqual(l1.ptPre, l2.ptPre, 1e-) ||
                    IsEqual(l1.ptPre, l2.ptNext, 1e-) ||
                    IsEqual(l1.ptNext, l2.ptPre, 1e-) ||
                    IsEqual(l1.ptNext, l2.ptNext, 1e-)) {

                    acutPrintf(L"存在重叠的部分\n");
                    return false;
                }
                else {
                    acutPrintf(L"存在平行的部分\n");
                    return false;

                }
            }
            else {

                double k2 = (y3 - y2) / (x3 - x2);

                double b2 = (y2 - k2*x2);

                AcGePoint2d jd;

                jd.x = x0;
                jd.y = k2*x0 + b2;

                double distance = l1.ptPre.distanceTo(l1.ptNext);
                double dis1 = jd.distanceTo(l1.ptPre);
                double dis2 = jd.distanceTo(l1.ptNext);

                if (dis1 < distance&&dis2 < distance) {

                    if (IsEqual(l1.ptPre, jd, 1e-) ||
                        IsEqual(jd, l2.ptNext, 1e-) ||
                        IsEqual(l1.ptNext, jd, 1e-) ||
                        IsEqual(jd, l2.ptPre, 1e-)) {

                        return false;
                    }

                    ptCenter.x = jd.x;
                    ptCenter.y = jd.y;
                    ptCenter.z = ;

                    return true;

                }
                else {
                    return false;
                }
            }
        }
        else if (x3 - x2 == ) {
        if (x0 - x1 != )
        {
            double k2 = (y1 - y0) / (x1 - x0);

            double b2 = (y1 - k2*x1);

            AcGePoint2d jd;

            jd.x = x3;
            jd.y = k2*x3 + b2;

            double distance = l1.ptPre.distanceTo(l1.ptNext);
            double dis1 = jd.distanceTo(l1.ptPre);
            double dis2 = jd.distanceTo(l1.ptNext);

            if (dis1 < distance&&dis2 < distance) {

                if (IsEqual(l1.ptPre, jd, 1e-) ||
                    IsEqual(jd, l2.ptNext, 1e-) ||
                    IsEqual(l1.ptNext, jd, 1e-) ||
                    IsEqual(jd, l2.ptPre, 1e-)) {

                    return false;
                }

                ptCenter.x = jd.x;
                ptCenter.y = jd.y;
                ptCenter.z = ;

                return true;

            }
            //交点在延长线上
            else {
                return false;
            }

        }
        else {
            if (IsEqual(l1.ptPre, l2.ptPre, 1e-) ||
                IsEqual(l1.ptPre, l2.ptNext, 1e-) ||
                IsEqual(l1.ptNext, l2.ptPre, 1e-) ||
                IsEqual(l1.ptNext, l2.ptNext, 1e-)) {

                acutPrintf(L"存在重叠的部分\n");
                return false;
            }
            else {
                acutPrintf(L"存在平行的部分\n");
                return false;
            }
        }
        }
        else {

            double k1 = (y1 - y0) / (x1 - x0);

            double b1 = (y1 - k1*x1);

            double k2 = (y3 - y2) / (x3 - x2);

            double b2 = (y2 - k2*x2);

            AcGePoint2d jd;

            if (k1 == k2) {
                return false;
            }

            double x0 = (b2 - b1) / (k1 - k2);
            jd.x = x0;

            jd.y = k1*x0 + b1;

            double distance = l1.ptPre.distanceTo(l1.ptNext);
            double dis1 = jd.distanceTo(l1.ptPre);
            double dis2 = jd.distanceTo(l1.ptNext);

            if (dis1 < distance&&dis2 < distance) {

                if (IsEqual(l1.ptPre, jd, 1e-) ||
                    IsEqual(jd, l2.ptNext, 1e-) ||
                    IsEqual(l1.ptNext, jd, 1e-) ||
                    IsEqual(jd, l2.ptPre, 1e-)) {

                    return false;
                }
                ptCenter.x = jd.x;
                ptCenter.y = jd.y;
                ptCenter.z = ;

                return true;
            }
            else {
                return false;
            }
        }
  }