324. 摆动排序 II（三路划分算法）

题目：

给定一个无序的数组 nums，将它重新排列成 nums[0] < nums[1] > nums[2] < nums[3]... 的顺序。

示例 1:

输入: nums = [1, 5, 1, 1, 6, 4]
输出: 一个可能的答案是 [1, 4, 1, 5, 1, 6]
示例 2:

输入: nums = [1, 3, 2, 2, 3, 1]
输出: 一个可能的答案是 [2, 3, 1, 3, 1, 2]
说明:
你可以假设所有输入都会得到有效的结果。

进阶:
你能用 O(n) 时间复杂度和 / 或原地 O(1) 额外空间来实现吗？

O(nlogn)的解法：

想到了先排序然后取前半部后半部交叉赋值，但第41个用例过不去，是一个[4,5,5,6]，看了大佬的解答，将两部分倒置再穿插赋值，这样就可以避免中间相邻的两个元素（前半部最大的数a和后半部最小的数b）相等的情况，因为两边分别倒置后，a在最前，b在最后，不会再组成一对插入新数组，很巧妙，另外还要注意c+的reverse是[begin,end)半闭半开区间，

 1 void wiggleSort(vector<int>& nums)
 2 {
 3     int siz = nums.size();
 4     sort(nums.begin(), nums.end());
 5     vector<int>temp(nums.size(),0);
 6     reverse(nums.begin(), nums.begin() + (siz - 1) / 2+1);
 7     reverse(nums.begin() + (siz - 1) / 2+1, nums.end());
 8     int i=0,m = 0, n = (siz - 1) / 2 + 1;
 9     for (;n<siz;++m,++n)
10     {
11         temp[i++] = nums[m];
12         temp[i++] = nums[n];
13     }
14     if (m == (siz - 1) / 2)
15     {
16         temp[i] = nums[m];
17     }
18     nums = temp;
19 }

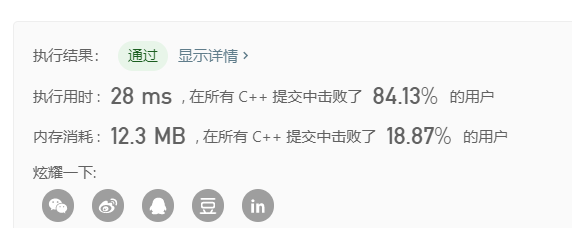
O(n)的解法：

前面排序后交叉赋值的方法做完后，应该可以想到前半段和后半段中并不要求严格有序，只要前面比后面的数都小就行，内部顺序其实无所谓。

那么就考虑用划分的方法，只要前面比后面小即可。

但普通快排用的划分是不行的，我们需要把数组分为恰好两半以交叉赋值回原数组。所以我们先要找中位数，再把这个中位数作为划分的基准数进行划分，这样划分出来的数组左右长度就应该是一样的。

中位数可以利用STL的nth_element()函数，时间O(N)。

然后简单的一次划分就行了吗？答案是某些情况可以（即中位数只出现一次的情况），但多数情况不可以。比如这个数组：[1,3,2,2,3,1]

其长度为6，中位数是2，对其做一次正常划分，下面这段代码是算法导论上的partition函数：

//之前先swap(nums[n/2],nums[ri])，以将基准数换为求好的中位数(n为数组长度）
 1 int partition_2(vector<int>& nums,int le,int ri){   //算法导论的方法
 2     int stable=nums[ri];
 3     int i=le-1,j=le;
 4     while(j<ri){
 5         if(nums[j]<stable){
 6             swap(nums[j],nums[++i]);
 7         }
 8         ++j;
 9     }
10     swap(nums[i+1],nums[ri]);
11     return i+1;
12 }

对其划分之后，数组为：1 1 2 3 3 2

可以看到，如果取该结果数组的前后各一半，进行交叉赋值是得不到摆动排序的数组的。原因是中位数2存在多个，我们的划分算法中对于nums[j]<=stable的处理（第6行）是简单的把小于基准数的数字都放到数组前面。最终的效果就是中位数和小于中位数的数字可能会乱序交叉在一起（例子中2，2，1，1就乱序了）。（当然如果我们划分算法里把小于等于基准数的数字都放到数组前面的话，那最终中位数同样的会可能和大于中位数的数字乱序交叉在一起。）我们希望的是中位数全部好好待在数组中部，左侧的数字都小于中位数，右侧的数字都大于中位数。那么就引出了一个新概念：三路划分，即将小于某个数的数字都排在左边，大于的都排在右边，中间的是该数字，不论它有几个。这个问题也就是https://leetcode-cn.com/problems/sort-colors/

下面是本题正确划分的代码：

其中i是最后一个小于中位数的数字的右侧，j是第一个小于中位数的数字的左侧，换句话：[0,i)是小于中位数的，[i,j]是等于中位数的，(j,n-1]是大于中位数的

经过如下划分算法，我们就可以避免上述的问题，还是上面的数据，经过一次划分后，数组为：1 1 2 2 3 3

int i=0,j=n-1,cur=0;
        while(cur<j){
            if(nums[cur]<mid){
                swap(nums[i++],nums[cur]);
            }
            else if(nums[cur]>mid){
                swap(nums[j--],nums[cur]);
            }
            ++cur;
        }

完整代码为：

 1 class Solution {
 2 public:
 3     void wiggleSort(vector<int>& nums) {
 4         int n=nums.size();
 5         nth_element(nums.begin(),nums.begin()+n/2,nums.end());
 6         int mid=nums[n/2];
 7         //划分
 8         int i=0,j=n-1,cur=0;
 9         while(cur<j){
10             if(nums[cur]<mid){
11                 swap(nums[i++],nums[cur]);
12             }
13             else if(nums[cur]>mid){
14                 swap(nums[j--],nums[cur]);
15             }
16             ++cur;
17         }
18         int l=n%2?n/2+1:n/2;
19         vector<int> p1(nums.begin(),nums.begin()+l);
20         vector<int> p2(nums.begin()+l,nums.end());
21         for(int i=0;i<p1.size();++i){
22             nums[2*i]=p1[p1.size()-i-1];
23         }
24         for(int i=0;i<p2.size();++i){
25             nums[2*i+1]=p2[p2.size()-i-1];
26         }
27     }
28 };

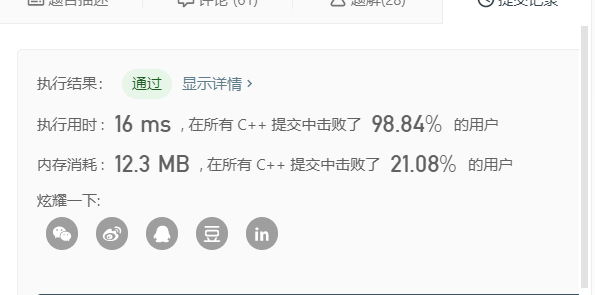
可以看到，划分算法更快：

完结撒花