多项式对数函数 - NTT

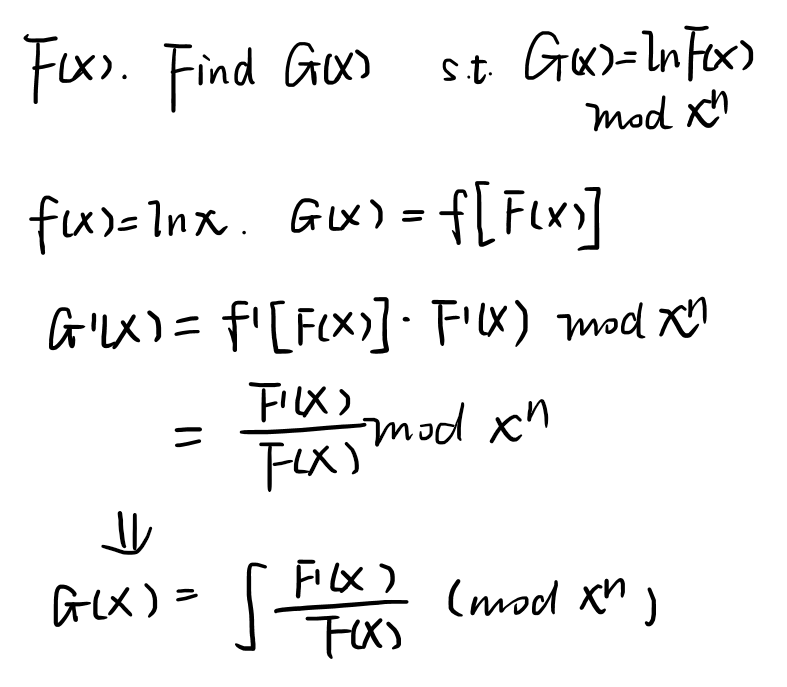
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=4000005; // 4 times!
const int mod=998244353,g=3;
int qpow(int p,int q) {
    int r = 1;
    for(; q; p*=p, p%=mod, q>>=1) if(q&1) r*=p, r%=mod;
    return r;
}
int inv(int p) {
    return qpow(p, mod-2);
}
namespace NTT {
    #define pw(n) (1<<n)
    const int N=4000005; // 4 times!
    const int mod=998244353,g=3;
    int n,m,bit,bitnum,a[N+5],b[N+5],rev[N+5];
    void getrev(int l){
        for(int i=0;i<pw(l);i++){
            rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
        }
    }
    int fastpow(int a,int b){
        int ans=1;
        for(;b;b>>=1,a=1LL*a*a%mod){
            if(b&1)ans=1LL*ans*a%mod;
        }
        return ans;
    }
    void NTT(int *s,int op){
        for(int i=0;i<bit;i++)if(i<rev[i])swap(s[i],s[rev[i]]);
        for(int i=1;i<bit;i<<=1){
            int w=fastpow(g,(mod-1)/(i<<1));
            for(int p=i<<1,j=0;j<bit;j+=p){
                int wk=1;
                for(int k=j;k<i+j;k++,wk=1LL*wk*w%mod){
                    int x=s[k],y=1LL*s[k+i]*wk%mod;
                    s[k]=(x+y)%mod;
                    s[k+i]=(x-y+mod)%mod;
                }
            }
        }
        if(op==-1){
            reverse(s+1,s+bit);
            int inv=fastpow(bit,mod-2);
            for(int i=0;i<bit;i++)a[i]=1LL*a[i]*inv%mod;
        }
    }
    void solve(vector <int> A,vector <int> B,vector <int> &C) {
        n=A.size()-1;
        m=B.size()-1;
        for(int i=0;i<=n;i++) a[i]=A[i];
        for(int i=0;i<=m;i++) b[i]=B[i];
        m+=n;
        bitnum=0;
        for(bit=1;bit<=m;bit<<=1)bitnum++;
        getrev(bitnum);
        NTT(a,1);
        NTT(b,1);
        for(int i=0;i<bit;i++)a[i]=1LL*a[i]*b[i]%mod;
        NTT(a,-1);
        C.clear();
        for(int i=0;i<=m;i++) C.push_back(a[i]);
        for(int i=0;i<=min(m*2,N-1);i++) a[i]=b[i]=0;
    }
}
struct poly {
    vector <int> a;
    void cut(int n) {
        while(a.size()>n) a.pop_back();
    }
    poly getcut(int n) {
        poly A=*this;
        A.cut(n);
        return A;
    }
    void read() {
        int n;
        cin>>n;
        for(int i=0;i<n;i++) {
            int t;
            cin>>t;
            a.push_back(t);
        }
    }
    void print() {
        for(int i=0;i<a.size();i++) cout<<a[i]<<" ";
        cout<<endl;
    }
    poly operator *(int b) {
        poly c=*this;
        for(int i=0;i<a.size();i++) (((c.a[i]*=b)%=mod)+=mod)%=mod;
        return c;
    }
    poly operator *(const poly &b) {
        poly c;
        NTT::solve(a,b.a,c.a);
        return c;
    }
    poly operator +(poly b) {
        int len=max(a.size(),b.a.size());
        a.resize(len);
        b.a.resize(len);
        poly c;
        for(int i=0;i<len;i++) c.a.push_back((a[i]+b.a[i])%mod);
        return c;
    }
    poly operator -(poly b) {
        int len=max(a.size(),b.a.size());
        a.resize(len);
        b.a.resize(len);
        poly c;
        for(int i=0;i<len;i++) c.a.push_back(((a[i]-b.a[i])%mod+mod)%mod);
        return c;
    }
    poly getinv(poly A, int n) {
        A.cut(n);
        poly B;
        if(n==1) {
            B.a.push_back(inv(A.a[0]));
        }
        else {
            poly Bi = getinv(A,(n-1)/2+1);
            B = Bi*2 - A*Bi*Bi;
            B.cut(n);
        }
        return B;
    }
    poly getinv() {
        int n=a.size();
        poly A=*this;
        return getinv(A,n);
    }
    poly getderi() {
        poly A=*this;
        poly B;
        for(int i=1;i<A.a.size();i++) B.a.push_back(A.a[i]*i%mod);
        return B;
    }
    poly getinte() {
        poly A=*this;
        poly B;
        B.a.push_back(0);
        for(int i=0;i<=A.a.size();i++) B.a.push_back(A.a[i]*inv(i+1)%mod);
        return B;
    }
    poly getln() {
        poly A=*this;
        int n=a.size();
        return (A.getderi()*A.getinv()).getinte().getcut(n);
    }
};
int n,a[N];
signed main() {
    ios::sync_with_stdio(false);
    poly A;
    A.read();
    A.getln().print();
}