记忆化搜索（DFS）--How many ways

How many ways

这是一个简单的生存游戏，你控制一个机器人从一个棋盘的起始点(1,1)走到棋盘的终点(n,m)。游戏的规则描述如下：
1.机器人一开始在棋盘的起始点并有起始点所标有的能量。
2.机器人只能向右或者向下走，并且每走一步消耗一单位能量。
3.机器人不能在原地停留。
4.当机器人选择了一条可行路径后，当他走到这条路径的终点时，他将只有终点所标记的能量,注意。

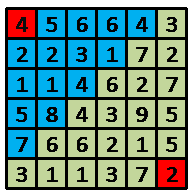
如上图，机器人一开始在(1,1)点，并拥有4单位能量，蓝色方块表示他所能到达的点，如果他在这次路径选择中选择的终点是(2,4)

点，当他到达(2,4)点时将拥有1单位的能量，这就是一种方式，并开始下一次路径选择，直到到达(6,6)点。
我们的问题是机器人有多少种方式从起点走到终点。这可能是一个很大的数，输出的结果对10000取模。

 

输入

第一行输入一个整数T,表示数据的组数。
对于每一组数据第一行输入两个整数n,m(1 <= n,m <= 100)。表示棋盘的大小。接下来输入n行,每行m个整数e(0 <= e < 20)。

 

输出

对于每一组数据输出方式总数对10000取模的结果.

 

样例输入

1
6 6
4 5 6 6 4 3
2 2 3 1 7 2
1 1 4 6 2 7
5 8 4 3 9 5
7 6 6 2 1 5
3 1 1 3 7 2

样例输出

每次的搜索函数dfs（）原理是一样的

附代码：

 #include <iostream>
 #include <cstring>
 #include <cstdio>
 #include <algorithm>
 using namespace std;
 int dp[][];
 int book[][];
 int m,n;

 int dfs(int x,int y)
 {
     int s=;
     if(x == n- && y == m-)
     {//如果到了终点返回1给s，让 s 加一
         return ;
     }
     if(book[x][y]>=)
     {//如果这个点已经走过了，并且知道从这个点到终点所有的路的总条数
         return book[x][y];//再次经过这个点的时候不用再搜索从这个点到终点路的条数，直接返回从这个点到终点所有的路的总条数
     }
     for(int i=;i<=dp[x][y];i++)//当作X的坐标
     {
         for(int j=;j<=dp[x][y];j++)//当作Y的坐标
         {
         //x 和 y 的变化量的总和不能大于当前位置的总能量
         //不能出界并且不搜索第一个位置
             if(i+j<=dp[x][y] && i+j!= && dp[x][y]> && x+i<n && y+j<m)
             {
                 s += dfs(x+i,y+j);//返回的是当前的点的下一个点所有的到终点的总路数
                 s %= ;//取后四位
             }
         }
     }
     book[x][y] = s;//当前点的总条数
     return s;//返回给调用此次搜索的地方
 }

 int main()
 {
     int T;
     cin >> T;
     while(T--)
     {
         cin >> n >> m;
         for(int i=;i<n;i++){
             for(int j=;j<m;j++){
                scanf("%d",&dp[i][j]);//dp[i][j]的值是每一格的能量
             }
         }
         memset(book,-,sizeof(book));
         //int total = dfs(0,0);//起始位置
         cout << dfs(,)% << endl;
     }
     return ;
 }