机器学习实战之k-近邻算法（3）---如何可视化数据

关于可视化：

《机器学习实战》书中的一个小错误，P22的datingTestSet.txt这个文件，根据网上的源代码，应该选择datingTestSet2.txt这个文件。主要的区别是最后的标签，作者原来使用字符串‘veryLike’作为标签，但是Python转换会出现ValueError: invalid literal for int() with base 10: 'largeDoses'的错误。所以改成后面的文件就可以了。后面直接用1 2 3 代表not like， general like, very like。这个错误一开始用百度查不到，改用Google（反向代理），第二个链接就是。哎。。。国内啊。。。

1. from numpy import *
2. import operator
3. #创建数据集
4. def createDataSet():
5. group = array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]])
6. labels = ['A', 'A', 'B', 'B']
7. return group, labels
8. #根据输入测试实例进行k-近邻分类
9. def classify0(inX, dataSet, labels, k):
10. dataSetSize = dataSet.shape[0]
11. diffMat = tile(inX, (dataSetSize, 1)) - dataSet
12. sqDiffMat = diffMat ** 2
13. sqDistances = sqDiffMat.sum(axis=1)
14. distances = sqDistances**0.5
15. sortedDistIndicies = distances.argsort()
16. classCount = {}
17. for i in range(k):
18. voteIlabel = labels[sortedDistIndicies[i]]
19. classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
20. sortedClassCount = sorted(classCount.iteritems(), key = operator.itemgetter(1), reverse=True)
21. return sortedClassCount[0][0]
22. #处理输入格式问题，从文件中读取数据
23. def file2matrix(filename, dim2):
24. fr = open(filename)
25. arrayOLines = fr.readlines()
26. numberOfLines = len(arrayOLines)
27. returnMat = zeros((numberOfLines, dim2))
28. classLabelVector = []
29. index = 0
30. for line in arrayOLines:
31. line = line.strip()
32. listFromLine = line.split('\t')
33. returnMat[index, :] = listFromLine[0:dim2]
34. classLabelVector.append(int(listFromLine[-1]))
35. index += 1
36. return returnMat, classLabelVector

1. >>>import kNN
2. >>> reload(kNN)
3. <module 'kNN' from 'kNN.pyc'>
4. >>> datingDataMat, datingLabels = kNN.file2matrix('datingTestSet2.txt', 3)

得到了约会网站的数据之后，我们可以可视化出来。

利用Matplotlib创建散点图，python(x, y)内嵌这个，直接import即可。

1. >>> mimport matplotlib.pyplot as plt
2. >>> fig = plt.figure()
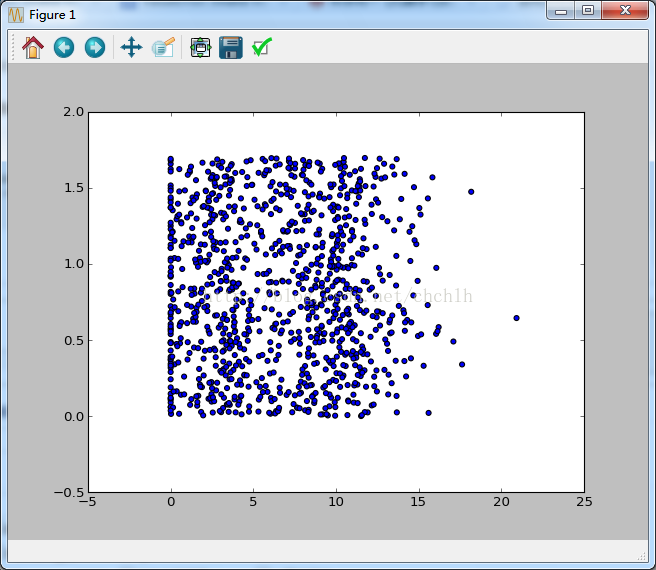
3. >>> ax = fig.add_subplot(111) >>> ax.scatter(datingDataMat[:,1], datingDataMat[:,2])
4. >>> plt.show()

这个是“玩视频游戏消耗时间比”和“每周所消费的冰淇淋公升数”的二维图。

需要不同的颜色来得到更好的可视化效果。

scatter函数的使用。

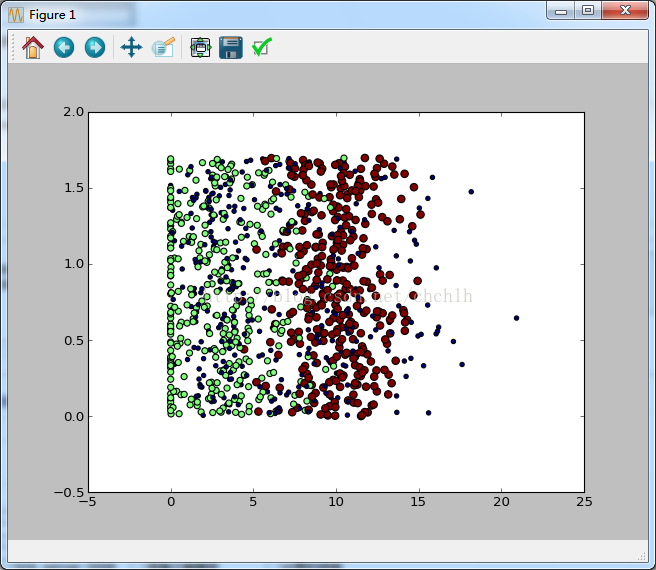
1. ax.scatter(datingDataMat[:,1], datingDataMat[:, 2], 15.0*array(datingLabels), 15.0*array(datingLabels))

这句代码替换前面的对应代码，如果出现name 'array' is not defined ,请在前面加这句:

1. from numpy import *

下面是青色，暗红色，黑色三种点，是利用了15 *　datingLabels的1， 2， 3作为不同点的颜色和尺寸。