转载：reverb

https://blog.csdn.net/qiumingjian/article/details/43938687

https://blog.csdn.net/jsjwangmingmin/article/details/58095888

https://wenku.baidu.com/view/547cb701a6c30c2259019e64.html

https://wenku.baidu.com/view/a856682bf4335a8102d276a20029bd64783e6297.html

所谓混响就是声音的直达声与反射声很紧凑的重合在一起时人耳所听到的声音，这个效果在语音的后期处理时特别有用。能产生混响最常见的场景就是房间内，尤其是空旷的房间中。

混响有直达声，早期反射和后期反射声组成。其中直达声是声源信号不经过任何障碍物直接到达人耳的那部分、早期反射声由一次或者几次反射的声音信号组成、后期反射声由随后更多次的反射声音信号组成。混响效果的空间感主要由早期反射声决定。

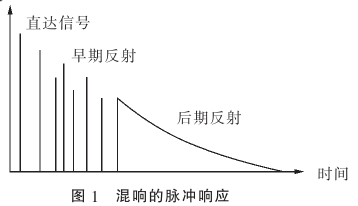
1.梳状滤波器

由于每次反射都会因为墙壁、障碍物等吸收一部分能量，所以声音信号的能量呈指数衰减。因此混响信号可以看成由直达声与许多逐步衰减、不断延迟的回声信号叠加而成，很自然的想到可以利用等比数列求和来进行模拟混响:

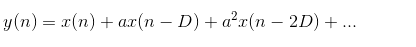
这里x(n)为原始声音信号、y(n)为混响信号、a为衰减系数、D为延迟时间。写成传递函数为：

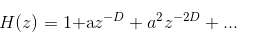
由等比数列求和公式，传递函数可以转换为：

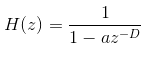
熟悉信号处理的朋友可能会比较眼熟，这不正是梳状滤波器吗？一点没错！正是IIR梳状滤波器。

如果写成差分方程，可表示为：

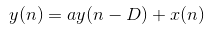
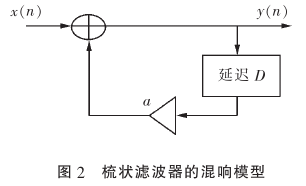
其典型的频谱特性为：

a=0.5, D=8.

B=[1 zeros(1, 7)];

A=[1 zeros(1, 6) -0.5];

[H, w]= freqz(B, A, 400, 'whole');

Hf=abs(H)

Hx=angle(H)

clf

figure(1)

plot(w, Hf)

figure(2)

plot(w, Hx)

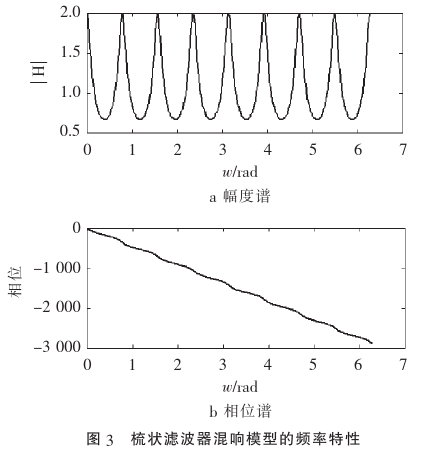
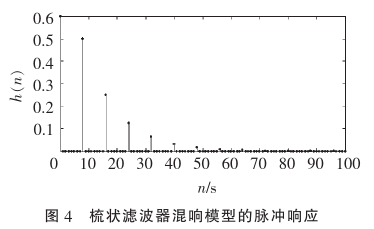
梳状滤波器频谱曲线不平坦，呈现明显的梳状效应，从而对不同的频率成分幅度产生波动，导致有金属声染色效应，听起来不够自然，另外，单纯使用梳状滤波器，其回声密度还是不够多。

2.全通滤波器

全通滤波器既有信号的延时效应，频谱又比较平坦。全通滤波器模型是在梳状滤波器模型的基础上，通过增加一条前向反馈支路实现的。

一阶全通传递函数可以表示为：

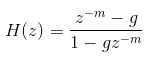
差分方程：

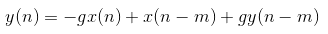
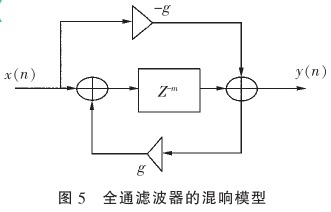
m=8, g=0.5，其频谱特性：

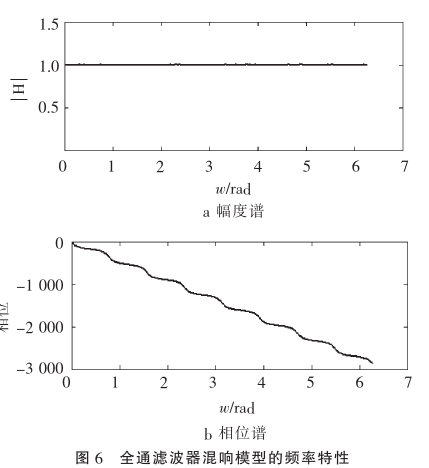
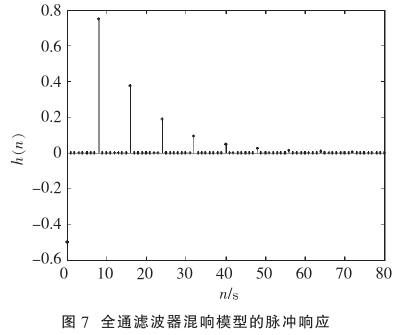
由全通滤波器的幅频特性可知，其频域相应幅度呈现直通分布；从梳状滤波器的脉冲响应可知，其冲击响应点离散的以m为间隔延续，且能量逐渐减小，因此与Reverb物理特性相一致。但是其回声密度同样受限于延迟时间，因此回声密度较低。

3 Schroeder混合模型
 综合梳状滤波器和全通滤波器，为了实现较高的回声密度，将4个梳状滤波器进行并联，然后通过2个级联的全通滤波器，实现Schroder混合模型。

梳状滤波器提供了混响效果中延时较长的回声，而延时较短的全通滤波器则起到了增加反射回声的密度的作用。在不同的滤波器中采用不同的延时可以使回声密度加大，并产生典型的具有早期反射和后期反射声的脉冲响应。通过将梳状滤波器的延时取得不规则，各个滤波器的频谱的峰谷不重叠，又避免了由于梳状滤波频谱不平坦造成的金属染色效应。

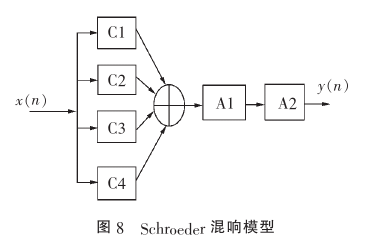
C1~C4为梳状滤波器，其延时时间取29.23ms, 37.67ms, 41.49ms, 44.31.ms

A1~A2为全通滤波器，延时取5ms， 1.7ms， 反馈增益取0.7， 0.7.

其频率响应如下

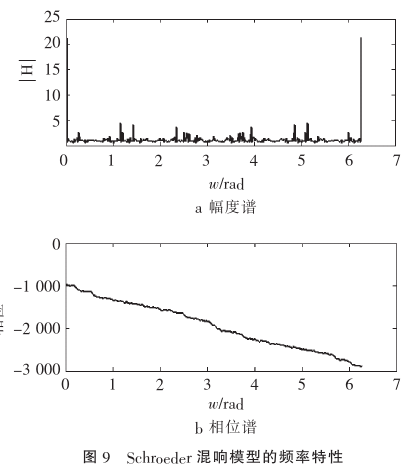
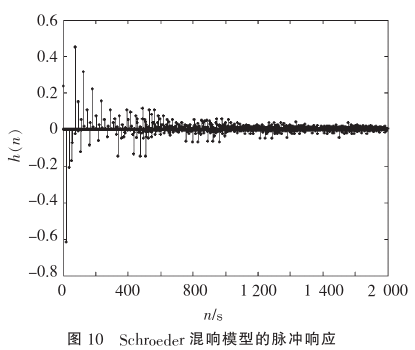
根据“Natural Sounding Artificial Reverberation”原文，混响时间与延时和衰减系数的关系为：T60=3*Td / (-log(a)).

混响时间定义为衰减60db的时间，Td为延时时间，a为衰减系数。

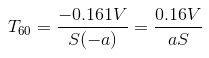
V　　　　　房间的体积，单位为立方米

S　　　　 房间的总表面积，单位为平方米

a为墙壁的吸声系数，那么则有（1-a）部分的声能被反射回来，并作用于下一次反射，且每一次都有a部分声能被吸收