转载:Laplace 变换
转自:
https://www.zhihu.com/question/22085329
https://wenku.baidu.com/view/691d4629640e52ea551810a6f524ccbff121cac4.html
https://wenku.baidu.com/view/fc07dd563b3567ec102d8a52.html
https://wenku.baidu.com/view/501b7d11336c1eb91a375dbe.html?from=search
定义:
连续时间傅里叶变换的公式是:
这里的是实数。
傅里叶变换要求时域信号绝对可积,即
为了让不符合这个条件的信号,也能变换到频率域,我们给x(t)乘上一个指数函数,
为任意实数。
可以发现,这个函数,就满足了绝对可积的条件,即
关于为什么
满足绝对可积条件,这里提一下,感性地说,我们知道负指数函数随t的增大,趋于零的速度是所有函数中最快的,这也是为什么我们描述某个现象暴涨的时候会说指数上升。因此大多数一般的函数
乘上某个负指数函数之后,一定绝对可积。
用更加严谨的数学表达,对于大多数,
,使得
是
的高阶无穷小。即
。因此在
的压迫下,
就满足了绝对可积的条件。
于是这个新函数的傅立叶变换就是:
化简得
显然是一个复数,我们把这个复数定义为一个新的变量——复频率,记为s。
于是便得到了拉普拉斯变换的公式:
所以拉普拉斯变换与连续时间傅里叶变换的关系是:拉普拉斯变换将频率从实数推广为复数,因而傅里叶变换变成了拉普拉斯变换的一个特例。当s为纯虚数时,x(t)的拉普拉斯变换,即为x(t)的傅里叶变换。
传递函数:
对于最简单的连续时间输入信号 x(t), 和输出信号 y(t)来说传递函数 H(s)所反映的就是零状态条件下输入信号的拉普拉斯变换X(s) 与输出信号的拉普拉斯变换 Y(s) 之间的线性映射关系:

系统收敛条件:
传递函数可以分解为以下形式:

Sp为r重极点,Si为一阶极点。
反变换得到系统冲激响应:

当极点在jw左半平面时,系统是稳定的(收敛)。










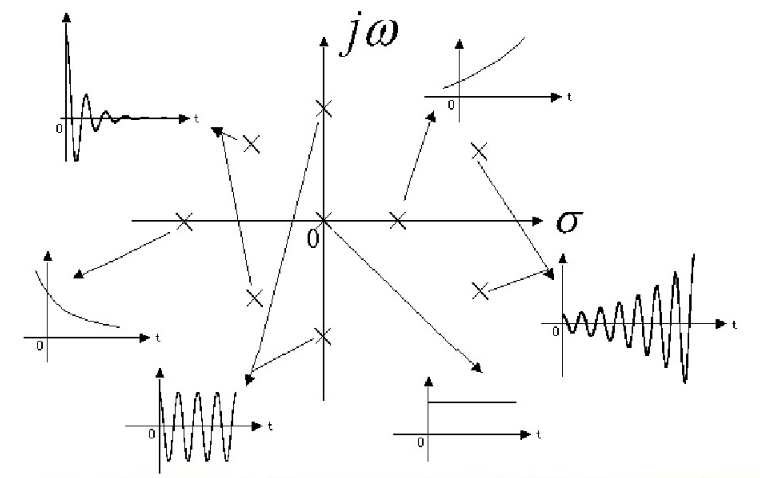
系统频率响应:
s=jw,即为系统的傅里叶变换,即为系统的频率响应。频率响应函数可以表示成零极点的形式。
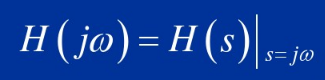


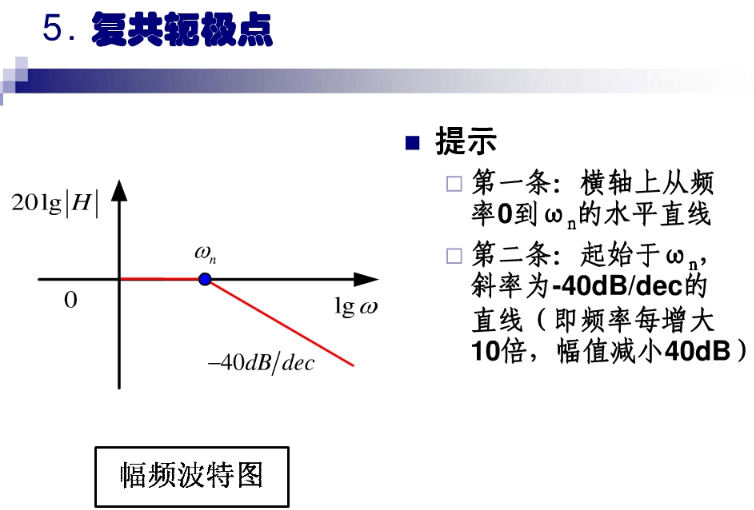
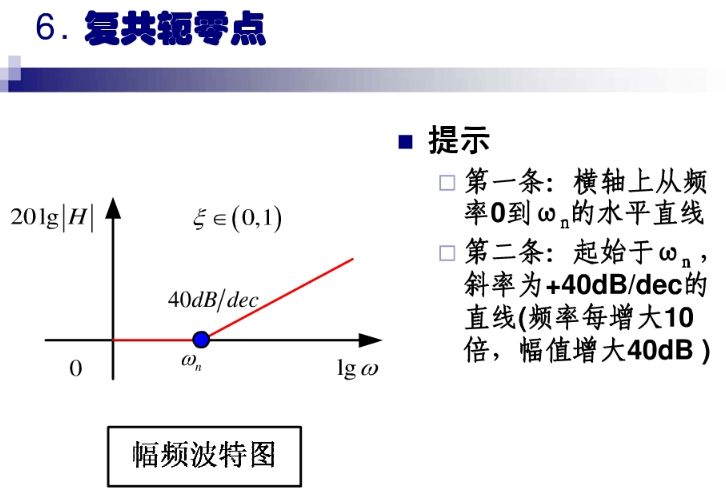
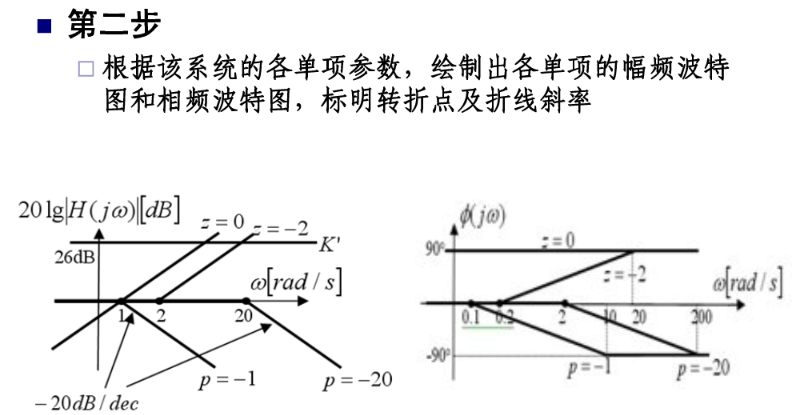
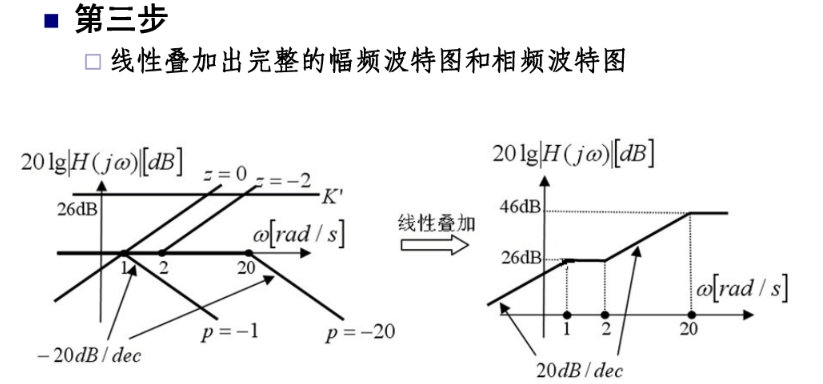
波特图:

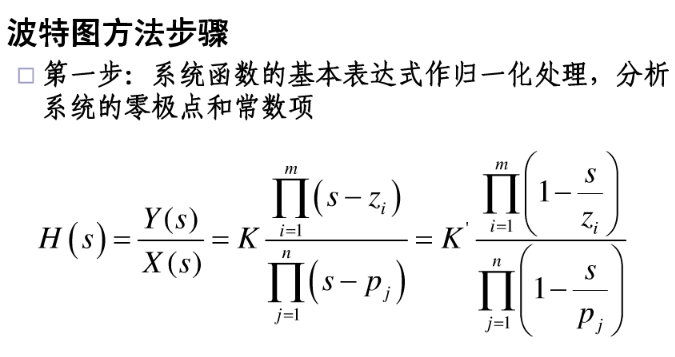
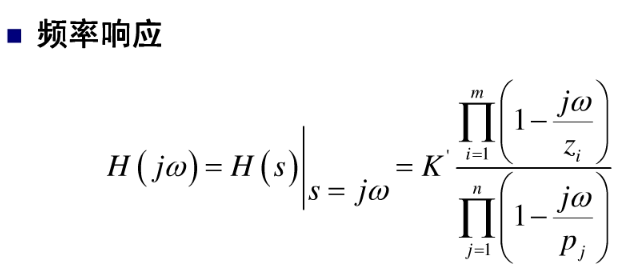


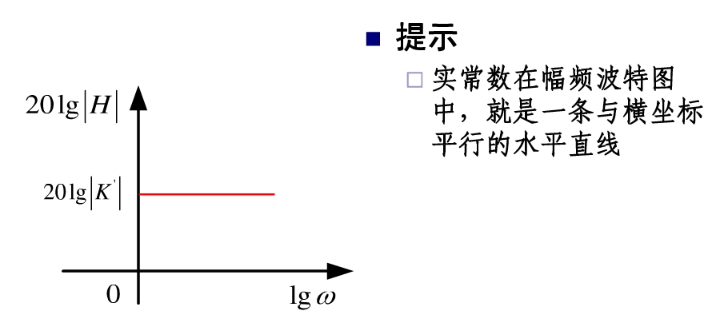

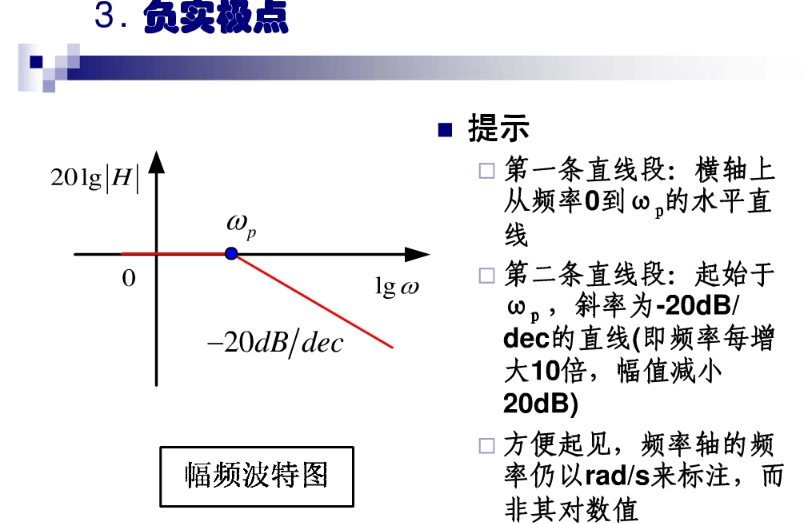
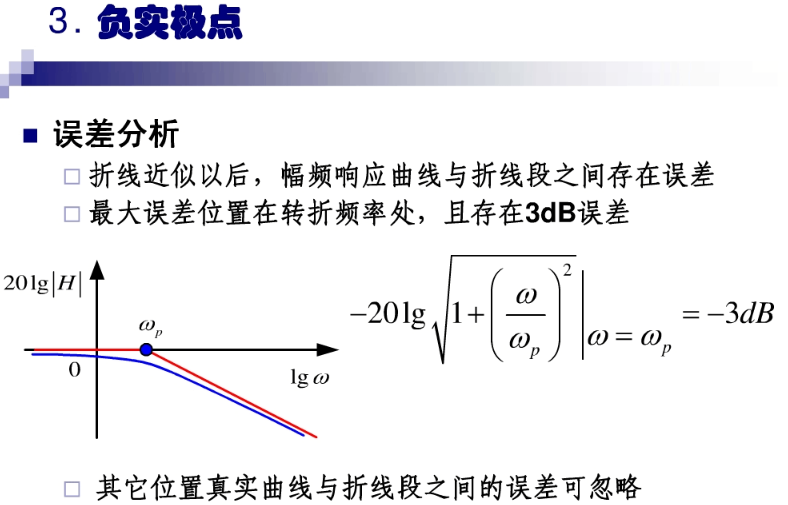


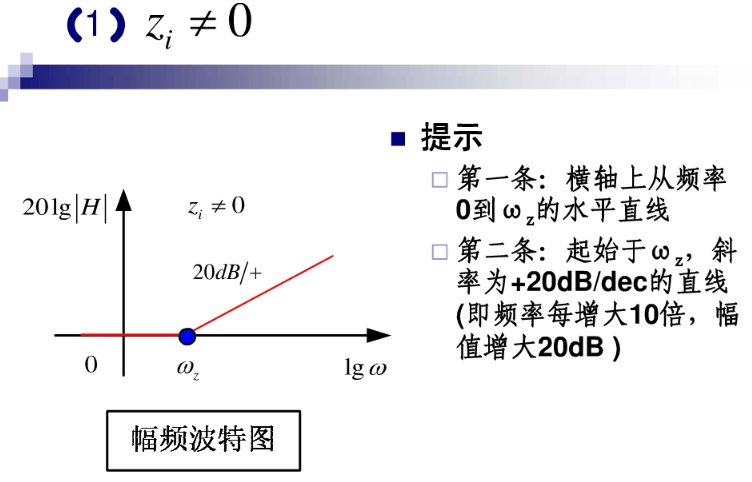
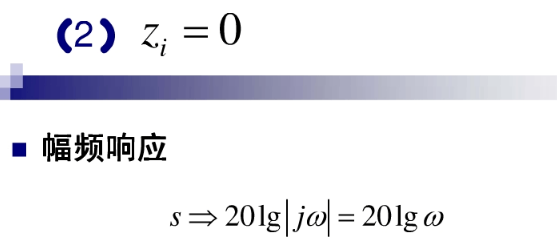





转载:Laplace 变换的更多相关文章
- 数理方程:Laplace变换 & 留数(更新中)
更新:25 APR 2016 Laplace变换 设函数\(f(t)\)在\(t>0\)时有定义,积分 \(F(s)=\int_0^{+\infty}f(t)e^{-st}dt \qquad ( ...
- Laplace变换要点
Laplace变换在求解微分方程.信号系统.自动控制领域都有重要作用.阅读<复变函数与积分变换>华中科大第三版,小结要点. 方便应用,最先给出变换表: 定义: 性质: 周期函数与卷积:
- 【OpenCV新手教程之十二】OpenCV边缘检測:Canny算子,Sobel算子,Laplace算子,Scharr滤波器合辑
本系列文章由@浅墨_毛星云 出品,转载请注明出处. 文章链接:http://blog.csdn.net/poem_qianmo/article/details/25560901 作者:毛星云(浅墨) ...
- [OpenCV入门教程之十二】OpenCV边缘检测:Canny算子,Sobel算子,Laplace算子,Scharr滤波器合辑
http://blog.csdn.net/poem_qianmo/article/details/25560901 本系列文章由@浅墨_毛星云 出品,转载请注明出处. 文章链接:http://blog ...
- 13. 用Roberts、Sobel、Prewitt和Laplace算子对一幅灰度图像进行边缘检测。观察异同。
#include <opencv2/opencv.hpp> #include<opencv2/highgui/highgui.hpp> #include<opencv2/ ...
- [转载] MATLAB快捷键
原文地址,点此查看 一.常用对象操作 除了一般windows窗口的常用功能键外. 1.!dir 可以查看当前工作目录的文件. !dir& 可以在dos状态下查看. 2.who 可以查看当前 ...
- 学习 opencv---(11)OpenC 边缘检测:Canny算子,Sobel算子,Laplace算子,Scharr滤波器
本篇文章中,我们将一起学习OpenCV中边缘检测的各种算子和滤波器——Canny算子,Sobel算子,Laplace算子以及Scharr滤波器.文章中包含了五个浅墨为大家准备的详细注释的博文配套源代码 ...
- [转] MATLAB快捷键
原文地址:MATLAB快捷键大全 (转载)作者:掷地有声 一.索引混排版 备注:删除了如F1(帮助)等类型的常见快捷命令 SHIFT+DELETE永久删除 DELETE删除 ALT+ENTER属性 A ...
- MATLAB命令大全
一.常用对象操作:除了一般windows窗口的常用功能键外.1.!dir 可以查看当前工作目录的文件. !dir& 可以在dos状态下查看.2.who 可以查看当前工作空间变量名, whos ...
随机推荐
- Oracle 12c 如何在 PDB 中添加 SCOTT 模式(手工方式)
Oracle 12c 建库后,没有 scott 模式,本篇使用手工脚本方式,在12c版本中创建 scott 模式及相关表. 目录 1. PDB中创建用户 2. PDB中用户授权 3. PDB中创建表空 ...
- pip问题:Traceback (most recent call last): File "/usr/bin/pip", line 9, in
源作者blog https://blog.csdn.net/vmxhc1314/article/details/81869676 编辑提示的文件,进行更改即可. 解决方法: 将 /usr/bin/pi ...
- source insight增加tab标签页的方法之sihook
1.效果如下 2.方法见如下博客 http://www.cnblogs.com/Red_angelX/archive/2013/01/23/2873603.html
- Windows2008r2、正版安装包
最近发现有很多人找我要Windows 2008的安装包,为了方便,就分享在这儿一下,有需要的自行下载. 链接:https://pan.baidu.com/s/1YZFE7FxL8O_gtfAftcX ...
- laravel框架api路由
Route::group(['namespace' => 'Api'], function (){ Route::any('send','SmsController@send'); }); gr ...
- MySQL的修改和删除数据表字段
MySQL的修改和删除数据表字段 写在前面: 数据库存在的意义:数据存储和数据管理. 数据库:行(数据),列(字段) 注意:本页是解决了列的字段问题.下一页是解决行的数据问题. 注意,所有的字段名,最 ...
- Application Characteristics Of LED Keychain
LED keychains are essential camping and travel accessories. Very useful as a light source. There are ...
- 常用的H5代码
1.返回上一页第一次在手机端用到返回上一页的时候,只写了window.history.go(-1):这一句.但是只在安卓手机有效果,兼容苹果手机需要在跳转代码后加上return false:这句.跳转 ...
- Spring-session+Redis解决Session共享
1. 保证Redis启动 2. 导入依赖 SpringBoot+Spring-Session+Redis <!--spring boot 与re ...
- MySql 存储大量长字节 Text报错处理办法
今天线上版本的错误: Caused by: com.mysql.jdbc.exceptions.jdbc4.MySQLSyntaxErrorException: Row size too large ...
