OpenCASCADE 平面求交

OpenCASCADE 平面求交

eryar@163.com

OpenCASCADE提供了类IntAna_QuadQuadGeo用来计算两个二次曲面quadric（球面、圆柱面、圆锥面及平面，平面是二次曲面的特例）之间的交线。他们之间可能的结果有：

l 一个点

l 一条或两条直线

l 一个点和一条直线

l 圆

l 椭圆

l 抛物线

l 双曲线

将源码结合《高等数学》、《解析几何》等书，可以来学习如何将理论付诸实践。本文主要介绍这个类中两个平面求交的源码实现。从源码中也可以看出OpenCASCADE官方开发人员的编码习惯。

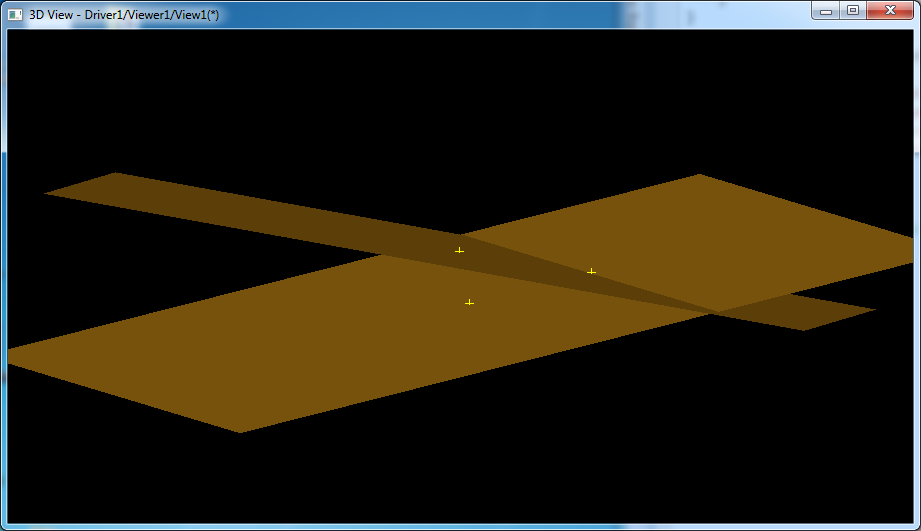
将源码列出如下：

void IntAna_QuadQuadGeo::Perform (const gp_Pln& P1,
                                  const gp_Pln& P2,
                                  const Standard_Real TolAng,
                                  const Standard_Real Tol)
{
  Standard_Real A1, B1, C1, D1, A2, B2, C2, D2, dist1, dist2, aMVD;
  //
  done=Standard_False;
  param2bis=.;
  //
  P1.Coefficients(A1,B1,C1,D1);
  P2.Coefficients(A2,B2,C2,D2);
  //
  gp_Vec aVN1(A1,B1,C1);
  gp_Vec aVN2(A2,B2,C2);
  gp_Vec vd(aVN1.Crossed(aVN2));
  //
  const gp_Pnt& aLocP1=P1.Location();
  const gp_Pnt& aLocP2=P2.Location();
  //
  dist1=A2*aLocP1.X() + B2*aLocP1.Y() + C2*aLocP1.Z() + D2;
  dist2=A1*aLocP2.X() + B1*aLocP2.Y() + C1*aLocP2.Z() + D1;
  //
  aMVD=vd.Magnitude();
  if(aMVD <=TolAng) {
    // normalles are collinear - planes are same or parallel
    typeres = (Abs(dist1) <= Tol && Abs(dist2) <= Tol) ? IntAna_Same
      : IntAna_Empty;
  }
  else {
    Standard_Real denom, denom2, ddenom, par1, par2;
    Standard_Real X1, Y1, Z1, X2, Y2, Z2, aEps;
    //
    aEps=.e-;
    denom=A1*A2 + B1*B2 + C1*C2;
    denom2 = denom*denom;
    ddenom = . - denom2;

    denom = ( Abs(ddenom) <= aEps ) ? aEps : ddenom;

    par1 = dist1/denom;
    par2 = -dist2/denom;

    gp_Vec inter1(aVN1.Crossed(vd));
    gp_Vec inter2(aVN2.Crossed(vd));

    X1=aLocP1.X() + par1*inter1.X();
    Y1=aLocP1.Y() + par1*inter1.Y();
    Z1=aLocP1.Z() + par1*inter1.Z();
    X2=aLocP2.X() + par2*inter2.X();
    Y2=aLocP2.Y() + par2*inter2.Y();
    Z2=aLocP2.Z() + par2*inter2.Z();

    pt1=gp_Pnt((X1+X2)*0.5, (Y1+Y2)*0.5, (Z1+Z2)*0.5);
    dir1 = gp_Dir(vd);
    typeres = IntAna_Line;
    nbint = ;
    //
    //-------------------------------------------------------
    // When the value of the angle between the planes is small
    // the origin of intersection line is computed with error
    // [ ~0.0001 ] that can not br considered as small one
    // e.g.
    // for {A~=2.e-6, dist1=4.2e-5, dist2==1.e-4} =>
    // {denom=3.4e-12, par1=12550297.6, par2=32605552.9, etc}
    // So,
    // the origin should be refined if it is possible
    //
    Standard_Real aTreshAng, aTreshDist;
    //
    aTreshAng=.e-; // 1.e-4 deg
    aTreshDist=.e-;
    //
    if (aMVD < aTreshAng) {
      Standard_Real aDist1, aDist2;
      //
      aDist1=A1*pt1.X() + B1*pt1.Y() + C1*pt1.Z() + D1;
      aDist2=A2*pt1.X() + B2*pt1.Y() + C2*pt1.Z() + D2;
      //
      if (fabs(aDist1)>aTreshDist || fabs(aDist2)>aTreshDist) {
        Standard_Boolean bIsDone, bIsParallel;
        IntAna_IntConicQuad aICQ;
        //
        // 1.
        gp_Dir aDN1(aVN1);
        gp_Lin aL1(pt1, aDN1);
        //
        aICQ.Perform(aL1, P1, TolAng, Tol);
        bIsDone=aICQ.IsDone();
        if (!bIsDone) {
          return;
        }
        //
        const gp_Pnt& aPnt1=aICQ.Point();
        //----------------------------------
        // 2.
        gp_Dir aDL2(dir1.Crossed(aDN1));
        gp_Lin aL2(aPnt1, aDL2);
        //
        aICQ.Perform(aL2, P2, TolAng, Tol);
        bIsDone=aICQ.IsDone();
        if (!bIsDone) {
          return;
        }
        //
        bIsParallel=aICQ.IsParallel();
        if (bIsParallel) {
          return;
        }
        //
        const gp_Pnt& aPnt2=aICQ.Point();
        //
        pt1=aPnt2;
      }
    }
  }
  done=Standard_True;
}

要理解这个源码，需要知道平面的一般方程：Ax+By+Cz+D=0，两个平面之间的夹角等概念。通过源码，可以看出计算两个平面之间的交线的步骤如下：

l 获取两个平面的一般方程的系数：A、B、C、D，其中平面的法向量（A,B,C)为单位向量；

l 将两个平面的法向量叉乘得到的向量vd为平面交线的方向；

l 分别计算一个平面上的点到另外一个平面的距离：dist1和dist2；

l 如果向量vd的大小小于指定的精度TolAng，则认为两个平面平行没有交线；如果两个距离dist1和dist2小于指定的精度Tol，则认为两个平面是相同的（重合）；

l 计算两个平面的夹角denom；

l 根据两个平面的夹角计算交线上的点；

l 后面是处理两个平面夹角很小的情况；

l 最后得到交线上的点pt1和方向dir1

其实上面求交线上点的代码不好理解，可以换成三个平面求交点的处理更好理解，如将交线的方向作为法向得到的一个平面与那两个平面一起计算交点，这个交点就一定在交线上，相关代码如下：

gp_Pln P3(vd.X(), vd.Y(), vd.Z(), 0.0);

IntAna_Int3Pln aTool(P1, P2, P3);
if (aTool.IsDone())
{
    pt1 = aTool.Value();
}

因为三个平面求交点是用高斯消元法解三元一次方程组，性能没有上面的代码好。生活中到处都是选择题，如何抉择是个问题啊。