MCMC&Gibbs sampling
Note of Markov Chain Monte Carlo and Gibbs Sampling : http://pan.baidu.com/s/1jHpWY1o
序:A major limitation towards more widespread implementation of Bayesian approaches is that obtaining thee posterior distribution often requires the integration of high-dimensional functions. Here the MCMC is used to solve this problem. There are two major method in the using of MCMC ---- Metropolis algorithm and Gibbs sampling.
- Monte Carlo Integration
问题:计算一个复杂积分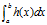
解决方案:把 分解成
分解成 和
和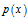 ,要求
,要求 是概率密度函数,得到
是概率密度函数,得到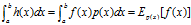 ,将函数积分转换为随机变量函数的期望进行计算。
,将函数积分转换为随机变量函数的期望进行计算。 ,这里的xi是服从概率分布密度为
,这里的xi是服从概率分布密度为 的随机变量x的取值。
的随机变量x的取值。
应用在贝叶斯理论中,后验概率 。
。
- Introduction to Markov Chain
介绍了马尔科夫过程,马尔可夫链,状态空间,转移概率,转移矩阵,以及切普曼-柯尔莫哥洛夫方程,平稳分布等概念。这里提及了从离散的平稳分布向连续状态进行过渡: à
à
- The Metropolis-Hasting Algorithm
问题:从复杂的概率分布p(x)中采样。
解决方案:假如我们要从p(x)=f(x)/K中采样,但是K 并不已知且无法求取,则采取如下方法进行采样
a.设定初始值x0,要满足f(x0)>0;
b.利用现在的x值,从转移分布q(x1,x2)中采样一个候选参数x*,对这个转移分布的限制是q(x1,x2)=q(x2,x1);
c.计算 (这里用的是比值所以可以避开K 进行计算);
(这里用的是比值所以可以避开K 进行计算);
d.如果alpha大于1则接受候选 x*;如果alpha小于1,则以概率alpha接受候选x*;然后返回到步骤b.
4. The Gibbs Sampler
这种采样方法应用在多变量的分布当中,在采样时,我们每次只对一个变量进行采样将其他变量固定。也就是说每次都是对一个单变量的条件分布进行采样,而不去理会联合分布,这样对n个变量进行轮流采样,进行k轮之后得到一个长度为k 的Gibbs Sequence 用来表示联合分布的采样。文章中的Example 4里列出了一个二维的联合分布的采样过程,他的两个条件分布分别为二项分布和Beta分布,很好的诠释 了Gibbs采样的流程和优势。
另外,这里还比较了吉布斯采样和EM算法的联系与区别。
EM每次都包含两个步骤:a.在固定参数下对隐变量求期望;b.固定隐变量的取值,利用极大似然的方法对参数数进行估计。
吉布斯采样则将隐变量和参数看成同等地位进行随机采样,可以看成是对EM算法的随机模拟。(原文:The Gibbs sampler can be thought of as a stochastic analog to the EM approaches used to obtain likelihood functions when missing data are present .)
参考:《统计学习方法》;
《Pattern recognition and machine learning 》第十一章 .
MCMC&Gibbs sampling的更多相关文章
- MCMC,GIBBS SAMPLING简单摘要
本文后面很多内容都是参考博客:http://www.cnblogs.com/xbinworld/p/4266146.html.本文主要用作学习交流备忘用. 1)简述: 随机模拟也可以叫做蒙特卡洛模拟, ...
- 随机采样方法整理与讲解(MCMC、Gibbs Sampling等)
本文是对参考资料中多篇关于sampling的内容进行总结+搬运,方便以后自己翻阅.其实参考资料中的资料写的比我好,大家可以看一下!好东西多分享!PRML的第11章也是sampling,有时间后面写到P ...
- 机器学习方法(八):随机采样方法整理(MCMC、Gibbs Sampling等)
转载请注明出处:Bin的专栏,http://blog.csdn.net/xbinworld 本文是对参考资料中多篇关于sampling的内容进行总结+搬运,方便以后自己翻阅.其实参考资料中的资料写的比 ...
- 随机采样方法整理与讲解(Acceptance-Rejection、MCMC、Gibbs Sampling等)
本文是对参考资料中多篇关于sampling的内容进行总结+搬运,方便以后自己翻阅.其实参考资料中的资料写的比我好,大家可以看一下!好东西多分享!PRML的第11章也是sampling,有时间后面写到P ...
- PRML读书会第十一章 Sampling Methods(MCMC, Markov Chain Monte Carlo,细致平稳条件,Metropolis-Hastings,Gibbs Sampling,Slice Sampling,Hamiltonian MCMC)
主讲人 网络上的尼采 (新浪微博: @Nietzsche_复杂网络机器学习) 网络上的尼采(813394698) 9:05:00 今天的主要内容:Markov Chain Monte Carlo,M ...
- 随机模拟MCMC和Gibbs Sampling
随机模拟 统计模拟中有一个重要的问题就是给定一个概率分布 p(x),我们如何在计算机中生成它的样本.一般而言均匀分布 Uniform(0,1)的样本是相对容易生成的. 通过线性同余发生器可以生成伪随机 ...
- 【转载】MCMC和Gibbs Sampling算法
转载随笔,原贴地址:MCMC和Gibbs Sampling算法 本文是整理网上的几篇博客和论文所得出来的,所有的原文连接都在文末. 在科学研究中,如何生成服从某个概率分布的样本是一个重要的问题.如果样 ...
- LDA-math-MCMC 和 Gibbs Sampling
http://cos.name/2013/01/lda-math-mcmc-and-gibbs-sampling/ 3.1 随机模拟 随机模拟(或者统计模拟)方法有一个很酷的别名是蒙特卡罗方法(Mon ...
- 随机采样和随机模拟:吉布斯采样Gibbs Sampling
http://blog.csdn.net/pipisorry/article/details/51373090 吉布斯采样算法详解 为什么要用吉布斯采样 通俗解释一下什么是sampling. samp ...
随机推荐
- java后台防止sql注入的方法
1.采用预编译语句集,它内置了处理SQL注入的能力,只要使用它的setString方法传值即可: String sql= "select * from users where usernam ...
- 使用eclipse创建第一个SpringBoot项目
1.new->maven->maven project, 勾选 Create a simple project, 下一个页面中填入group id(项目组织唯一标识, 如org.ap ...
- centos服务器cpu百分之百,top查询不到之“-bash”
把这条注释掉. [root@aaaa ~]# cat /etc/ld.so.preload #/usr/local/lib/libproc.so[root@aaaa ~]# 然后在top
- centos批量创建用户并发送邮件,(修订版)
# cat user_create.sh echo -n "创建用户输入C,删除用户输入D!" read name function monitor() { if [ " ...
- 小小知识点(二十二)显示屏与主机之间连接,出现无信号字样时,应检查是否正确选择集显和独显VGA接口
显示屏与主机之间连接,出现无信号字样时,应检查是否正确选择集显和独显VGA接口 通过VGA接口判断集成显卡和独立显卡.在台式机主机上,VGA接口竖着放置的说明是集成显卡,VGA接口横着放置的说明是独立 ...
- (01)hibernate框架环境搭建及测试
---恢复内容开始--- 1.创建javaweb项目 2.导包 hibernate包 hibernate\lib\required\*.jar 数据库驱动包 mysql-connector-java- ...
- DFT与IDFT
[转]https://blog.csdn.net/mingzhuo_126/article/details/88044390 二.编程实现考滤到DFT和IDFT算法过程中有部分相似,可以把它们合成到一 ...
- 【转】常见Java面试题 – 第二部分:equals与==
ImportNew注: 本文是ImportNew编译整理的Java面试题系列文章之一.你可以从这里查看全部的Java面试系列. Q2.下面的代码片段的输出是什么? Object s1 = new St ...
- mongodb学习(一)——简介和基本操作
简介 MongoDB 是一个基于分布式文件存储的数据库 属于NoSQL数据库,是介于关系数据库和非关系数据库之间的产品,是非关系数据库当中功能最丰富,最像关系数据库的 旨在为WEB应用提供可扩展的高性 ...
- P3802 小魔女帕琪 概率与期望
P3802 小魔女帕琪 题目背景 从前有一个聪明的小魔女帕琪,兴趣是狩猎吸血鬼. 帕琪能熟练使用七种属性(金.木.水.火.土.日.月)的魔法,除了能使用这么多种属性魔法外,她还能将两种以上属性组合,从 ...
