MT【285】含参数函数绝对值的最大值

(浙江2013高考压轴题)已知$a\in R$,函数$f(x)=x^3-3x^2+3ax-3a+3$
(2)当$x\in[0,2]$时,求$|f(x)|$的最大值.

分析:
由题意$f^{'}(x)=3x^2-6x+3a$
当$\Delta=36(1-a)\ge0$时,可求得极值点$x_1=1-\sqrt{1-a},x_2=1+\sqrt{1-a}$
(注:考虑到$x\in[0,2]$ 故只需考虑$0\le a\le1$时)
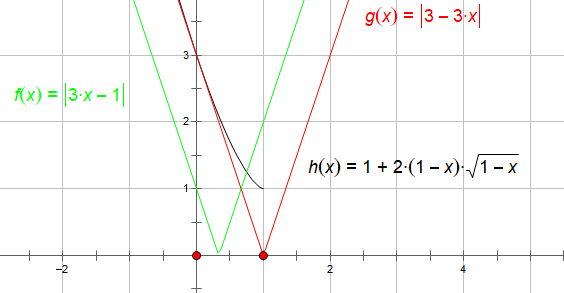
对应极值为$f(x_1)=1+2(1-a)\sqrt{1-a},f(x_2)=1-2(1-a)\sqrt{1-a}$
(注:求极值时用$x^2=2x-a$降次后再代入)
由$f(x_1)+f(x_2)=2>0,f(x_1)-f(x_2)=4(1-a)\sqrt{1-a}>0$得
$f(x_1)\ge|f(x_2)|$
$\because \max\{|f(x)\}=\max\{|f(x)_{min}|,|f(x)_{max}|\}$
故只需考虑
$\max\{|f(x)|\}=\max\{|f(0)|,|f(2)|,|f(x_1)|\}=\max\{|3-3a|,|3a-1|,1+2(1-a)\sqrt{1-a}\}$
由图像可得
$$\max\{|f(x)\}=
\begin{cases}
3-3a,&x\le0\\
1+2(1-a)\sqrt{1-a},&0<x<\dfrac{3}{4}\\
3a-1,&x\ge\dfrac{3}{4}\\
\end{cases}$$

注:
$|f(x)|$的最大值的题型要想到用画图去做.

题中$g(a)=1+2(1-a)\sqrt{1-a},(0<a<1)$的图像可以由$y=2a^{\frac{3}{2}}$变换得到