最短路（Floyd）-hdu1317

题目链接：https://vjudge.net/problem/HDU-1317

题目描述：

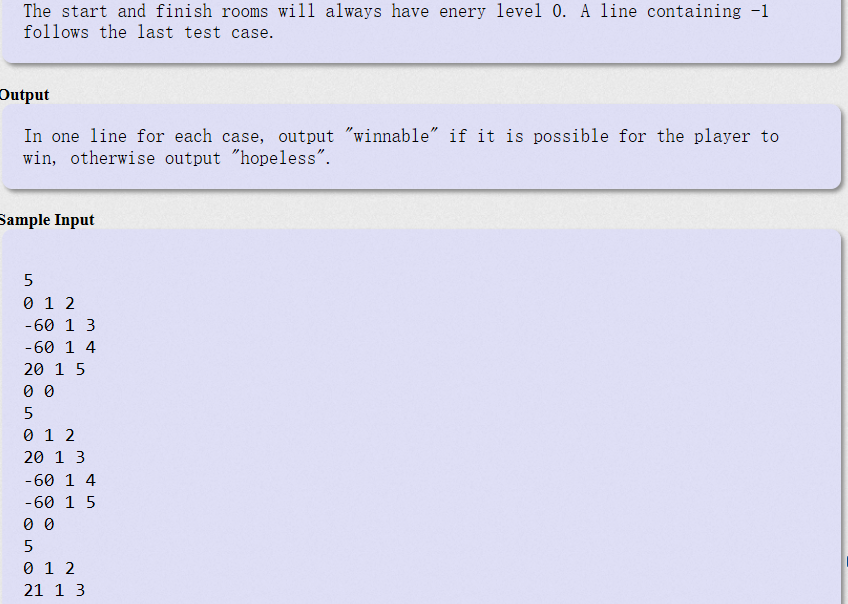
　　题意：玩家起始有100个能量点，刚开始在起始房间中，每个房间外有一条单向的路径通往其他房间（一个房间可能通往多个房间），具体通往哪些房间可以查看房间门口的房间列表。每次玩家进入一个房间，他的能量值会更新成 当前自身能量值+房间能量值（重点是房间的能量值可能为负值）。玩家想要终止游戏的话，要么是能够进入到终点房间，要么是因能量耗尽而累死。需要我们判断玩家能否进入到终点房间。

　　Floyd算法（Floyd-Warshall algorithm）又称为弗洛伊德算法、插点法，是解决给定的加权图中顶点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。（百度百科）

　　因为此题中存在负权值，因此用Floyd最短路来解决。

　　思路：首先我们需要检查是否存在这样的路从1到达N，如果不存在，直接输出hopeless。我们可以利用floyd算法去检查。Floyd-Warshall算法是一种在具有正或负边缘权重（但没有负周期）的加权图中找到最短路径的算法。因为题中可能会出现负周期——行成环路，可以无限增加能量值。但是可以用于检查1到N是否连通。然后我们再使用Bellman算法，如果松弛N-1次后，任然存在更新。说明图中存在负周期，说明能量可以无限叠加，检查环路的点是否与N连通就行了。如果不存在负周期，则检查到达N的能量是否大于0。转载自博文：https://blog.csdn.net/rainbow_storm/article/details/81263440

代码实现：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int N,M;
const int MAXN =;
const int INF = 0x3f3f3f3f;
/*    d数组表示到达i房间的最大的能量值；
    p数组表示每个房间的能量值；
    G数组存图。G[i][j]=1，表示i到j有1条通路。
    E数组存边。
*/
struct edge{
    int from,to;
}E[MAXN*MAXN];
int d[MAXN],P[MAXN];
int G[MAXN][MAXN];
bool floyd()//判断是否房间之间是可达的，如不可达，则输出hopeless
{
    for(int k=;k<=N;k++)
        for(int i=;i<=N;i++)
            for(int j=;j<=N;j++)
                if(G[i][k]&&G[k][j])
                    G[i][j]=;
    return G[][N];
}
 
bool bellman(){
    fill(d,d+MAXN,-INF);
    d[]=;//初始值为100
    for(int i=;i<N;i++)
    {
        bool flag=false;
        for(int j=;j<M;j++){
            if(d[E[j].to] < d[E[j].from]+P[E[j].to] && d[E[j].from]+P[E[j].to]>){
                flag=true;
                d[E[j].to]=d[E[j].from]+P[E[j].to];
            }
        }
        if(!flag) break;
    }
    for(int j=;j<M;j++){
        if(d[E[j].to] < d[E[j].from]+P[E[j].to] && d[E[j].from]+P[E[j].to]>){
            d[E[j].to]=d[E[j].from]+P[E[j].to];
            if(G[E[j].to][N]){
                return true;
            }
        }
    }
    return d[N]>;
}
 
int main(){
    while(~scanf("%d",&N)&&(N!=-)){
        memset(G,,sizeof(G));
        memset(E,,sizeof(E));
        memset(P,,sizeof(P));
        M=;
        int con;//记录连接多少扇门
        for(int i=;i<=N;i++){
            scanf("%d%d",&P[i],&con);
            for(int j=;j<=con;j++){
                int tmp;scanf("%d",&tmp);
                E[M++]=(edge){i,tmp};
                G[i][tmp]=;//说明从门i到门tmp是可达的
            }
        }
        if(!floyd()){
            printf("hopeless\n");
            continue;
        }
        if(bellman()){
            printf("winnable\n");
        }else{
            printf("hopeless\n");
        }
    }
    return ;
}