PID控制器开发笔记之三：抗积分饱和PID控制器的实现

积分作用的引入是为了消除系统的静差，提高控制精度。但是如果一个系统总是存在统一个方向的偏差，就可能无限累加而进而饱和，极大影响系统性能。抗积分饱和就是用以解决这一问题的方法之一。这一节我们就来实现抗积分饱和的PID算法。

1、抗积分饱和的基本思想

所谓积分饱和就是指系统存在一个方向的偏差，PID控制器的输出由于积分作用的不断累加而扩大，从而导致控制器输出不断增大超出正常范围进入饱和区。当系统出现反响的偏差时，需要首先从饱和区退出，而不能对反向的偏差进行快速的响应。

为了解决积分饱和的问题，人们引入了抗积分饱和的PID算法。所谓抗积分饱和算法，其思路是在计算U(k)的时候，先判断上一时刻的控制量U(k-1)是否已经超出了限制范围。若U(k-1)>Umax，则只累加负偏差；若U(k-1)<Umin，则只累加正偏差。从而避免控制量长时间停留在饱和区。

2、算法实现

抗积分饱和的思想很简单，解释在控制器输出的最大最小值附近限制积分的累积情况，以防止在恢复时没有响应。根据前面得分系我们可以得到如下的流程图：

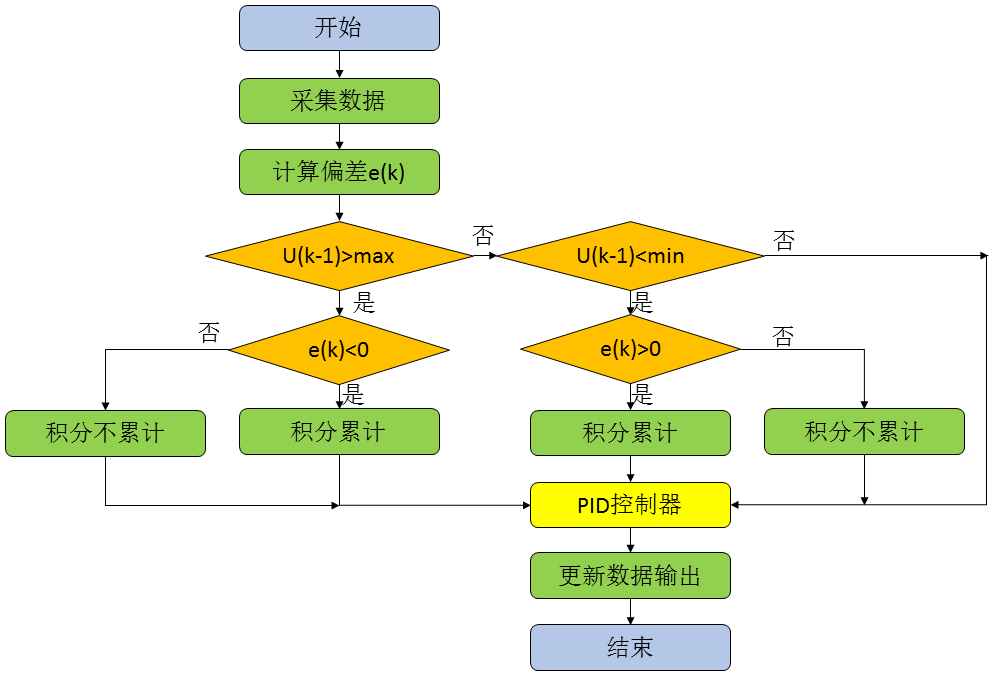
（1）位置型PID算法实现

对于位置型PID的抗积分饱和算法其实就是在基本的PID基础上加上抗积分饱和的操作，增加量个机锋的极限值。首先定义PID对象的结构体：

 /*定义结构体和公用体*/
 
 typedef struct
 
 {
 
   float setpoint;       //设定值
 
   float proportiongain;     //比例系数
 
   float integralgain;      //积分系数
 
   float derivativegain;    //微分系数
 
   float lasterror;     //前一拍偏差
 
   float result; //输出值
 
   float integral;//积分值
 
   float maximum;//最大值
 
   float minimum;//最小值
 
 }PID;

接下来实现PID控制器：

 void PIDRegulation(PID *vPID, float processValue)
 
 {
 
   float thisError;
 
   thisError=vPID->setpoint-processValue;
 
   if(vPID->result>vPID->maximum)
 
   {
 
     if(thisError<=)
 
     {
 
       vPID->integral+=thisError;
 
     }
 
   }
 
   else if(vPID->result<vPID->minimum)
 
   {
 
     if(thisError>=)
 
     {
 
       vPID->integral+=thisError;
 
     }
 
   }
 
   else
 
   {
 
     vPID->integral+=thisError;
 
   }
 
   vPID->result=vPID->proportiongain*thisError+vPID->integralgain*vPID->integral+vPID->derivativegain*(thisError-vPID->lasterror);
 
   vPID->lasterror=thisError;
 
 }

（2）增量型PID算法实现

增量型PID的抗积分饱和的实现也是一样在最基本的增量型PID算法中引入极大极小的限值，并在算法中通过比较限值实现抗饱和的操作。

首先定义PID对象的结构体：

 /*定义结构体和公用体*/
 
 typedef struct
 
 {
 
   float setpoint;       //设定值
 
   float proportiongain;     //比例系数
 
   float integralgain;      //积分系数
 
   float derivativegain;    //微分系数
 
   float lasterror;     //前一拍偏差
 
   float preerror;     //前两拍偏差
 
   float deadband;     //死区
 
   float result; //输出值
 
   float maximum;//最大值
 
   float minimum;//最小值
 
 }PID;

接下来实现PID控制器：

 void PIDRegulation(PID *vPID, float processValue)
 
 {
 
   float thisError;
 
   float increment;
 
   float pError,dError,iError;
 
   thisError=vPID->setpoint-processValue; //得到偏差值
 
   pError=thisError-vPID->lasterror;
 
   iError=;
 
   dError=thisError-*(vPID->lasterror)+vPID->preerror;
 
   if(vPID->result>vPID->maximum)
 
   {
 
     if(thisError<=)
 
     {
 
       iError=thisError;
 
     }
 
   }
 
   else if(vPID->result<vPID->minimum)
 
   {
 
     if(thisError>=)
 
     {
 
       iError=thisError;
 
     }
 
   }
 
   else
 
   {
 
     iError=thisError;
 
   }
 
   increment=vPID->proportiongain*pError+vPID->integralgain*iError+vPID->derivativegain*dError;   //增量计算
 
   vPID->preerror=vPID->lasterror;  //存放偏差用于下次运算
 
   vPID->lasterror=thisError;
 
   vPID->result+=increment;
 
 }

3、总结

所谓抗积分饱和就是防止由于长期存在一个方向的偏差而对相反方向的偏差迟滞响应。本文的方法是在达到极值后将不再对这一方向的偏差做出反应相反只对另一方向的偏差做出反应。事实上由于偏差的存在有可能造成输出值超限的情况，所以还需要对输出值作出限制。

欢迎关注：