OO第一单元(求导)单元总结

OO第一单元(求导)单元总结

　　这是我们oo课程的第一个单元，也是意在让我们接触了解掌握oo思想的一个单元，这个单元的作业以求导为主题，从一开始的加减多项式求导再到最后的嵌套多项式求导，难度逐渐提高，编程思想也逐步深入面向对象，如果说前两次作业还可以用C语言的面向过程的思想去对付，那么第三次作业可以说是为面向对象而设计的。

一、作业分析

　　1.第一次作业

　　　　第一次作业作业的目标是实现简单的加减多项式的求导，项的形式为带符号整数和幂函数的结合，带符号整数符号与数字间不允许有空格，如-3*x。

　　　　

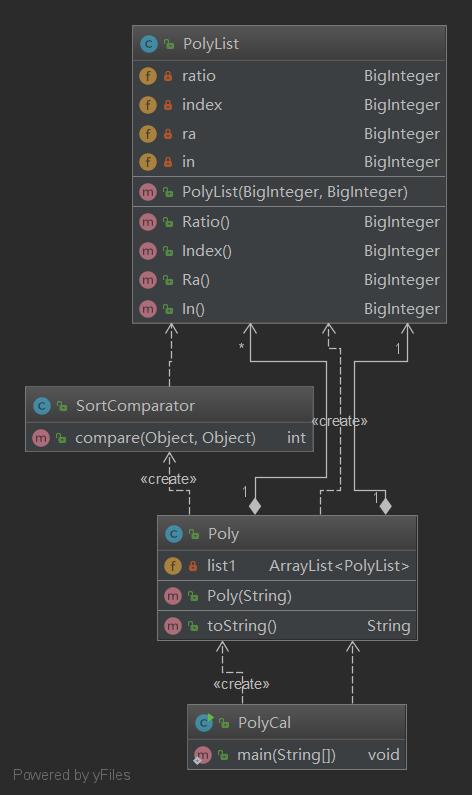
　　　　由于此次作业是我第一次接触面向对象（暴露我寒假没好好学Java），所以类的架构显得十分混乱，命名也乱七八糟。主类为PolyCal，它的功能是读入输入的数据并创建读入的多项式的Poly类对象，并且承担了一部分Poly类的toString功能（由于checkstyle对行数的规定导致写不下）。Poly类的功能是检查读入的字符串并进行处理，将其按项存入一个ArrayList中并排序以方便之后实现化简，以上功能全部由Poly的Construction方法完成，toString方法实现了求导后结果的输出。PolyList类其实应该命名为Item，它用来保存读入的项并完成求导。SortComparator类是用于ArrayList排序的类。

　　　　多项式求导的三次作业都可以划分为读入、求导、输出三大部分，每一部分都可以相互独立。第一次作业的读入是通过大正则实现的，先通过大正则判断输入多项式的格式是否正确，再通过小正则分离出项与每一项的系数和指数。求导部分由PolyList完成，由于题目要求简单，所以求导只是简单的公式求导。输出部分完成了对表达式的化简，通过排序后的ArrayList来合并同类项，并消除重复的符号，对空字符串特判等等已达到长度优化目的。

　　　　

　　　　

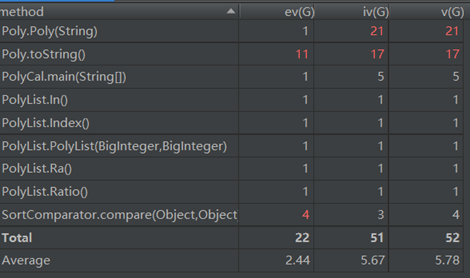
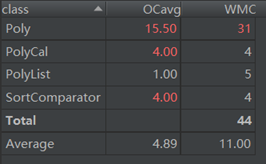
　　　　此次作业的优点就是不容易出错，其实这个说法有两面性，大正则写得好确实不容易出错，而是加上大部分人的Bug多是处在正则表达式上。而缺点就非常多，首先就是架构毫无延展性可言，其次类与类之间功能的分配也很混乱，可以说是一个长得像面向对象的面向过程工程。

　　　　程序出现的Bug：主要有两个，第一个是爆栈，这就是用大正则的副作用。第二个是空输入，由于我并没有再使用Scanner时用hasNextLine判断，所以读入空文件时会出错。

　　　　刀别人的策略：由于这次的作业简单，代码行数不是很多，所以读代码成为了一个可行的方法，可以将其他人的代码一行一行仔细研读，尤其是正则表达式要读的格外仔细。当然Wrong Format是这次作业互测必走的流程。

　　2.第二次作业

　　　　第二次作业相比第一次多了sin，cos两个三角函数和多项因子相乘，同时引入了因子和项的概念，表达式由任意数量项相加减组成，项由任意数量因子由乘法组成，三角函数保留字内不允许有空格。

　　　　

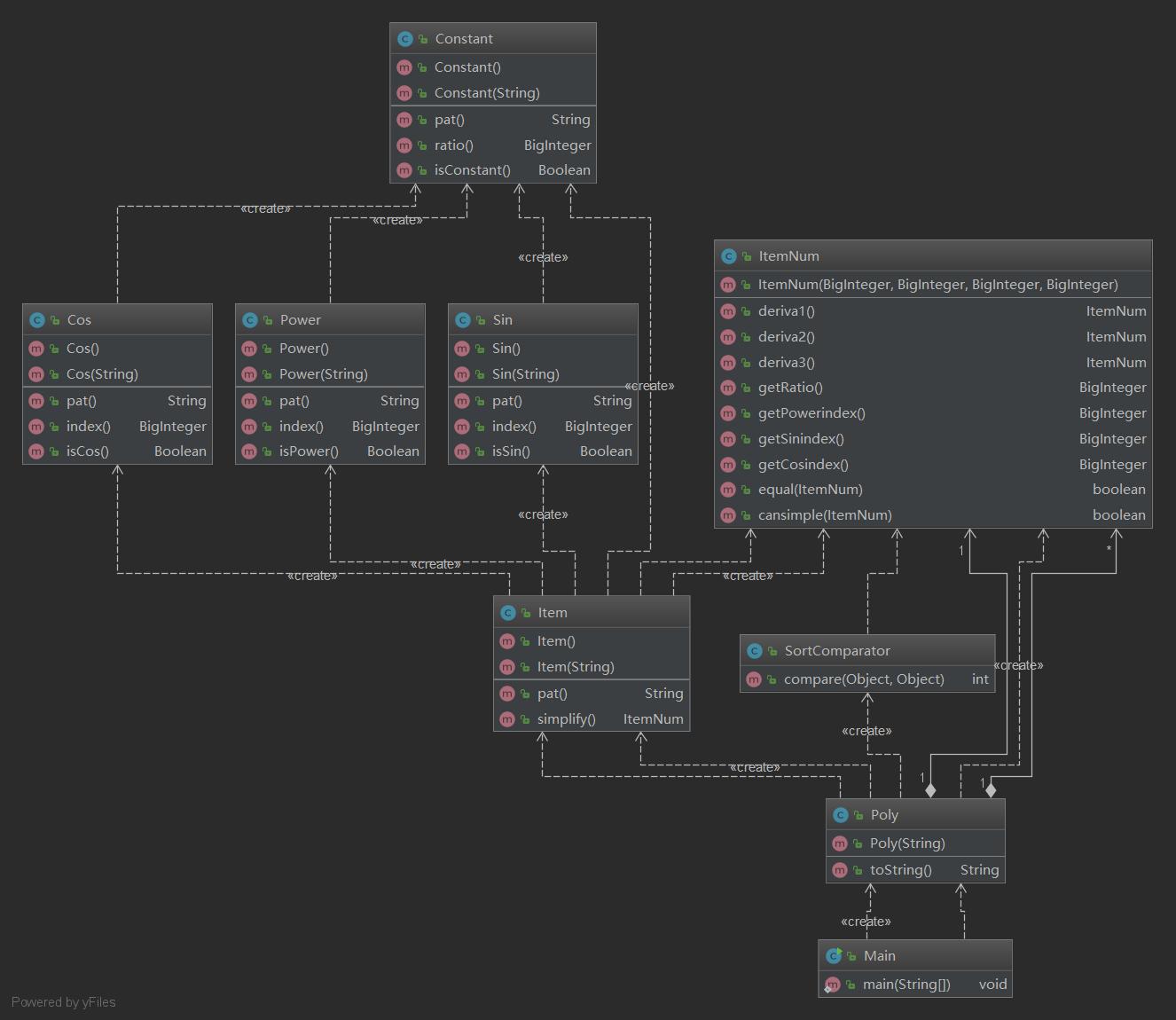
　　　　从这次作业的题目要求中不难看出题目有意引导我们构建面向对象并且具有一定延展性的工程，而我也尽力尝试去做了，但由于我对继承的掌握并不够熟练，所以没敢在这次作业中使用继承，但也写出了具有层次性的架构。第一层是表达式（Poly），第二层是项（Item，ItemNum），第三层是因子（Power，Constant，Sin，Cos）。

　　　　读入的实现依旧有正则表达式实现，但是这次与上次有所不同，吸取了上次爆栈的教训，这次的正则表达式是建立在逐项分析的基础上。每一个类都带有自己对应的正则表达式，并且用于组成上一级的正则表达式。求导则通过将每一项合并为a*x^b*sin(x)^c*cos(x)^d在进行对项的公式求导实现，这部分的实现由ItemNum类完成。输出则有Poly类的toString方法单独处理，而化简则由Item类的simplify方法单独处理。

　　　　

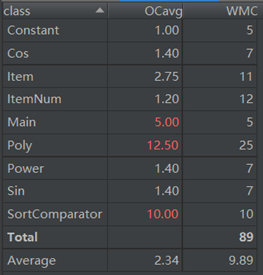
　　　　我这次作业的有点在于使用的方法比较简便，也有一定的延展性，相比上次作业也更像一个面向对象作业了。问题也很突出，事实（第三次作业）证明我所构建的框架还是太小，延展性还是不够，尤其是我所采用的求导方法可谓完全没有延展性，是只适用与这次作业的取巧的方法。

　　　　程序出现的Bug：这次Bug只有一个，比上次少，却导致我挂了更多的强测点。这次的Bug是我在优化时出现了问题，我用了String类的replaceAll方法将所有+1*换成了+，-1*换成了-，这就导致诸如x^-1*cos(x)会被有化成x^-cos(x)。

　　　　刀别人的策略：由于题目变难了，代码变长了，所以通读代码显得不那么现实，因此我采取了只看他们正则表达式的方法。而另一方面，我也用自己构建的样例来进行统一测试。

　　3.第三次作业

　　　　这次作业相比上次作业又多了表达式因子与嵌套求导，难度急剧提升。其中嵌套求导只会出现在三角函数中。

　　　　

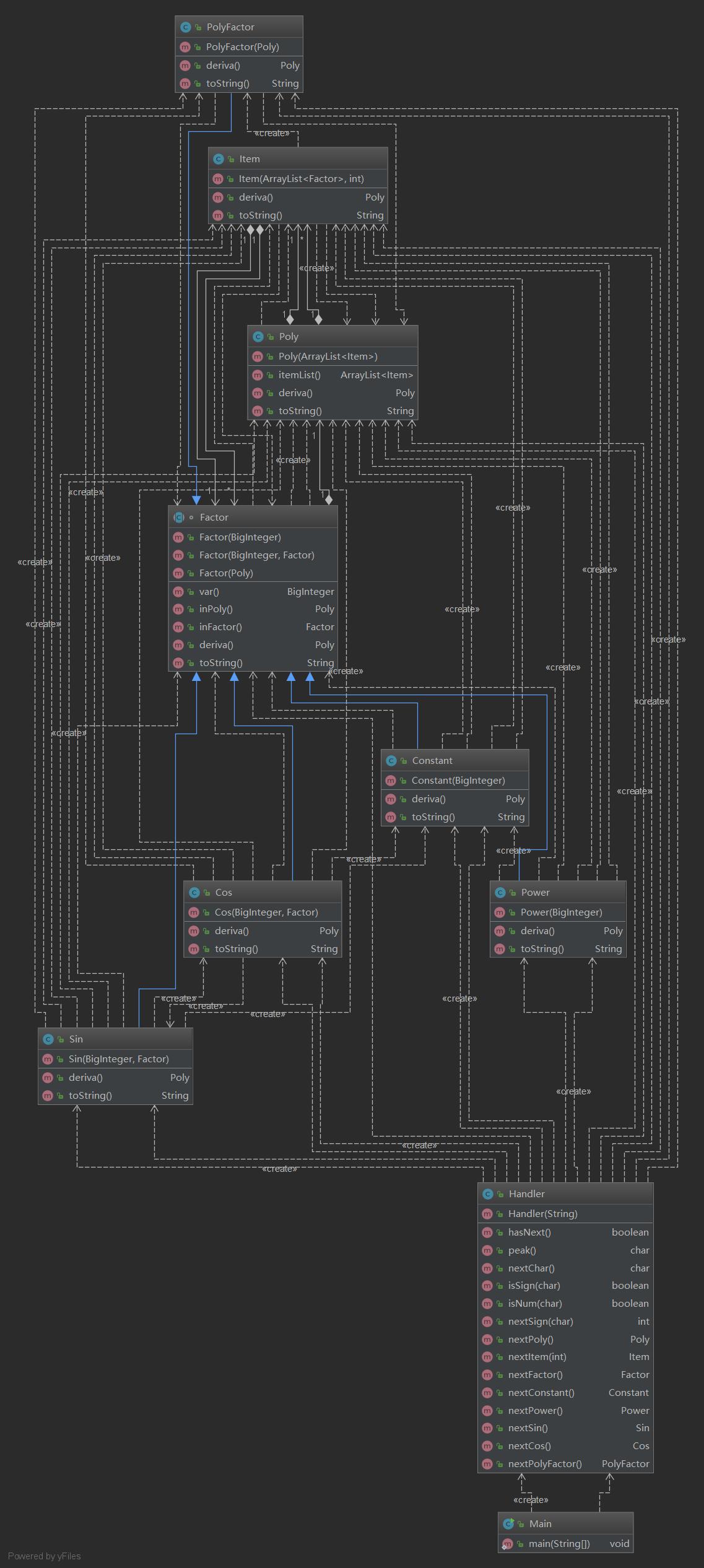
　　　　这次作业几乎是必须用面向对象的思想去完成了，和上次作业一样我采用三重式架构，第一层是多项式（Poly），第二层是项（Item），第三层是因子（父类Factor，子类Power，Constant，Sin，Cos，PolyFactor）。

　　　　读入我采用递归读入，并由Handler类单独处理。求导采用通过每个类之间与每个层级之间的调用来实现递归求导。同理输出也是递归输出，优化方面由于我所选用的球道和输出方法还有我比较菜所以就只优化了最基础的一些部分。

　　　　

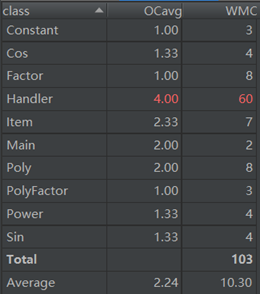
　　　　我这次作业的优点就是架构和方法比较清晰，每个类的职能明确。问题就是由于读入求导与输出都采用递归的方法所以对于多重嵌套的数据处理会非常慢从而导致超时。

　　　　程序出现的Bug：超时

　　　　刀别人的方法：这次是彻底不能靠读代码来刀人了，因此我学会了使用自动测试，并通过自动生成测试集来自动测试他人代码。

二、总结与感悟

　　面向对象的思想可以说是这个单元我最大的收获。从一开始的披着面向对象外皮的面向过程工程到最后的使用了继承的面向对象工程，我感受到我正一步步了解面向对象的思想内涵。面对一个新的工程，首先要思考的不是要完成事情的工序，而是这个工程所包含了那些对象，这些对象又各自拥有什么功能，哪些对象之间由is-a或has-a的关系。在完成这三次作业的过程中，我逐渐有以工序架构代码转变为由对象组成代码。当然作为一个面向对象的初心者，我的不足还是很明显，我的代码延展性非常的差，三次作业可以说是写了三次全新的代码，虽然我的架构能很好地完成当前的问题，但却对未来会出现的问题毫无准备，这也是我所欠缺的面向对象的素质。