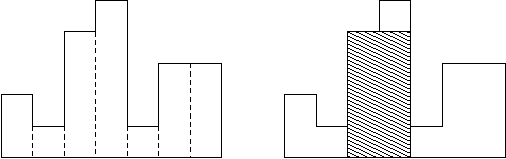
☆ [POJ2559] Largest Rectangle in a Histogram 「单调栈」

类型：单调栈

传送门：>Here<

题意：给出若干宽度相同的矩形的高度（条形统计图），求最大子矩形面积

解题思路

单调栈的经典题

显然，最终的子矩形高度一定和某一个矩形相等（反证）。因此一个暴力的做法就是枚举每一个矩形，然后往两边扩散。在它左侧找到第一个高度比它小的，右侧也一样。则可以求出最大可扩散宽度，乘上高度即可以更新答案。复杂度$O(n^2)$

如果说要优化刚才的算法，也就可以优化寻找最大可扩散宽度的速度

让每一个矩形依次入栈，保存两个关键字：矩形高度，其最大左扩散宽度。保证栈内的矩形高度单调递增

我们可以得到结论：目前栈内的一个矩形$u$，在原图中从$u$开始一直到栈顶所在的矩形，高度一定都比$u$高。这就是为什么我们不需要统计栈内矩形的最大右扩散宽度，因为最大右扩散宽度就是栈顶

再回忆一下最大左扩散宽度的意义，是在它左侧的高度大于它的矩形们。这让我们又得出一个结论：目前栈内的一个矩形$u$，如果它的最大左扩散宽度大于$1$，则这些它所能扩散到的矩形一定都不在栈中。这也很容易发现，因为栈是单调递增的。或者，我们可以得到一个更形象的结论：栈内连续的两个矩形$u,v$，如果在原图中他们之间有矩形，那么这些矩形一定都高于$u,v$

因此刚才我们所说的最大左扩散宽度，其实等同于在原图中，它到栈中上一个矩形之间相隔了多少矩形

当一个新的矩形进来的时候，它会弹走若干个矩形。而栈内一个矩形实际上代表着原图中一段矩形。因此可以说是弹走了几段矩形。但是这些被弹走的矩形只不过出栈，在原图中并不会消失。因此他们所代表的的宽度不应当消失，所以我们将他们累积在新进来的这个矩形上。这也非常符合事实——这个新的矩形之所以能弹走这若干个矩形是因为自己比他们矮，因此都可以扩散到。换句话说，被弹走的这一系列矩形最多只能向右扩散到这个新矩形，因此留着它们就没有意义了

而对于任何一个要出栈的矩形，我们需要统计由它的高度所能扩散出去的最大子矩形面积。由于它的最大左扩散宽度已知，唯一需要知道的就是它的最大右扩散宽度。那么由于它在栈里，它的最大右扩散宽度也就是从它一直到最早先的栈顶之间的宽度。因此我们只需要在弹栈的过程中一路累积每个出栈矩形的最大左扩散宽度，加起来就是这一段宽度了。

另外，如果处理完了最后一个矩形以后栈依然有剩余，则应当弹完并更新答案

保证了每个矩形入栈以及出栈恰好一次，在正确性显然的条件下，复杂度$O(n)$

Code

/*By DennyQi 2018.8.18*/
#include <cstdio>
#include <queue>
#include <cstring>
#include <algorithm>
#define  r  read()
#define  Max(a,b)  (((a)>(b)) ? (a) : (b))
#define  Min(a,b)  (((a)<(b)) ? (a) : (b))
using namespace std;
typedef long long ll;
#define int ll
const int MAXN = ;
const int INF = ;
inline int read(){
    int x = ; int w = ; register int c = getchar();
    while(c ^ '-' && (c < '' || c > '')) c = getchar();
    if(c == '-') w = -, c = getchar();
    while(c >= '' && c <= '') x = (x<<) + (x<<) + c - '', c = getchar();return x * w;
}
int N,H,top,cnt,ans;
int h[MAXN],w[MAXN];
#undef int
int main(){
#define int ll
    for(;;){
        N=r;
        if(!N) break;
        top = ;
        ans = ;
        for(int i = ; i <= N; ++i){
            H=r;
            if(!top || H > h[top]){
                h[++top] = H;
                w[top] = ;
            }
            else{
                cnt = ;
                while(top >  && H <= h[top]){
                    cnt += w[top];
                    ans = Max(ans, h[top] * cnt);
                    --top;
                }
                h[++top] = H;
                w[top] = cnt+;
            }
        }
        cnt = ;
        while(top > ){
            cnt += w[top];
            ans = Max(ans, h[top] * cnt);
            --top;
        }
        printf("%lld\n", ans);
    }
    return ;
}