全局最小割Stoer-Wagner算法

借鉴：http://blog.kongfy.com/2015/02/kargermincut/

提到无向图的最小割问题，首先想到的就是Ford-Fulkerson算法解s-t最小割，通过Edmonds–Karp实现可以在O(nm2)时间内解决这个问题（n为图中的顶点数，m为图中的边数）。

但是全局最小割和s-t最小割不同，并没有给定的指定的源点s和汇点t，如果通过Ford-Fulkerson算法来解这一问题，则需要枚举汇点t（共n−1），时间复杂度为O(n2m2)。

Can we do better?

答案是肯定的，Karger在攻读博士学位期间（Orz…）提出了非常著名的基于随机化的全局最小割算法，算法非常简单，简单到不敢相信它是正确的，算法描述如下：

1. 在图中随机取一条边，将边的两个端点合并（contraction），同时消除所有由于合并而形成自环的边

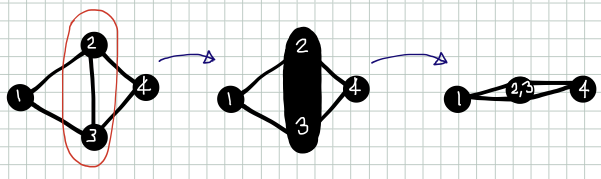
Contraction

1. 重复步骤1直到图中仅剩下两个点
2. 将最终两点之间的边作为找的割返回

合并的边权值相加

1.min=MAXINT，固定一个顶点P

2.从点P用“类似”prim的s算法扩展出“最大生成树”，记录最后扩展的顶点和最后扩展的边

3.计算最后扩展到的顶点的切割值（即与此顶点相连的所有边权和），若比min小更新min

4.合并最后扩展的那条边的两个端点为一个顶点（当然他们的边也要合并，这个好理解吧？）

5.转到2，合并N-1次后结束

6.min即为所求，输出min

　prim本身复杂度是O(n^2)，合并n-1次，算法复杂度即为O(n^3)，如果在prim中加堆优化，复杂度会降为O((n^2)logn)0.

#include <iostream>
#include <cstdio>
#include <sstream>
#include <cstring>
#include <map>
#include <cctype>
#include <set>
#include <vector>
#include <stack>
#include <queue>
#include <algorithm>
#include <cmath>
#include <bitset>
#define rap(i, a, n) for(int i=a; i<=n; i++)
#define rep(i, a, n) for(int i=a; i<n; i++)
#define lap(i, a, n) for(int i=n; i>=a; i--)
#define lep(i, a, n) for(int i=n; i>a; i--)
#define rd(a) scanf("%d", &a)
#define rlld(a) scanf("%lld", &a)
#define rc(a) scanf("%c", &a)
#define rs(a) scanf("%s", a)
#define rb(a) scanf("%lf", &a)
#define rf(a) scanf("%f", &a)
#define pd(a) printf("%d\n", a)
#define plld(a) printf("%lld\n", a)
#define pc(a) printf("%c\n", a)
#define ps(a) printf("%s\n", a)
#define MOD 2018
#define LL long long
#define ULL unsigned long long
#define Pair pair<int, int>
#define mem(a, b) memset(a, b, sizeof(a))
#define _  ios_base::sync_with_stdio(0),cin.tie(0)
//freopen("1.txt", "r", stdin);
using namespace std;
const int maxn = , INF = 0x7fffffff;

int n, m;
int way[maxn][maxn], d[maxn], bin[maxn];
bool vis[maxn];

int contract(int &s, int &t)
{
    mem(vis, false);
    mem(d, );
    int k, maxc, ans;
    rap(i, , n)
    {
        k = -, maxc = -INF;
        rap(j, , n)
            if(!bin[j] && !vis[j] && d[j] > maxc)
                k = j, maxc = d[j];
        if(k == -) return ans;
        s = t, t = k, ans = maxc;
        vis[k] = true;
        rap(j, , n)
            if(!bin[j] && !vis[j])
                d[j] += way[k][j];
    }
    return ans;
}

int SW()
{
    int mincut = INF, ans, s, t;
    rep(i, , n)
    {
        ans = contract(s, t);
        bin[t] = ;
        mincut = min(ans, mincut);
        if(mincut == ) return ;
        rap(j, , n)
            if(!bin[j])
                way[s][j] = (way[j][s] += way[j][t]);
    }
    return mincut;
}

int main()
{
    while(scanf("%d%d", &n, &m) != EOF)
    {
        mem(way, );
        mem(bin, );
        int u, v, w;
        rap(i, , m)
        {
            rd(u), rd(v), rd(w);
            u++, v++;
            way[u][v] += w;
            way[v][u] += w;
        }
        cout << SW() << endl;
    }

    return ;
}