浅谈分词算法（4）基于字的分词方法（CRF）

目录

• 前言
• 目录
• 条件随机场（conditional random field CRF）
  • 核心点
  • 线性链条件随机场
  • 简化形式
• CRF分词
• CRF VS HMM
• 代码实现
  • 训练代码
  • 实验结果
• 参考文献

前言

通过前面几篇系列文章，我们从分词中最基本的问题开始，并分别利用了1-gram和HMM的方法实现了分词demo。本篇博文在此基础上，重点介绍利用CRF来实现分词的方法，这也是一种基于字的分词方法，在将句子转换为序列标注问题之后，不使用HMM的生成模型方式，而是使用条件概率模型进行建模，即判别模型CRF。之后我们对CRF与HMM进行对比，同样的我们最终也会附上CRF分词的实现代码。

目录

浅谈分词算法（1）分词中的基本问题
浅谈分词算法（2）基于词典的分词方法
浅谈分词算法（3）基于字的分词方法（HMM）
浅谈分词算法（4）基于字的分词方法（CRF）
浅谈分词算法（5）基于字的分词方法（LSTM）

条件随机场（conditional random field CRF）

为了说清楚CRF在分词上的应用，我们需要简单介绍下条件随机场CRF，我们不去长篇大论的展开论述，只讨论几个核心的点，并重点阐述下线性链条件随机场，也是我们在序列标注问题中经常遇到的，如分词、词性标注、韵律标注等等。

核心点

在上一篇博文中，我们简单介绍了HMM模型，是一个五元组，它的核心围绕的是一个关于序列\(X\)和\(Y\)的联合概率分布\(P(X,Y)\)，而在条件随机场的核心围绕的是条件概率分布模型\(P(Y|X)\)，它是一种马尔可夫随机场，满足马尔科夫性（这里我们就不展开阐述了，具体可参考[3]）。我们这里必须搬出一张经典的图片，大家可能在网上的无数博文中也都看到过，其来源与[4]：

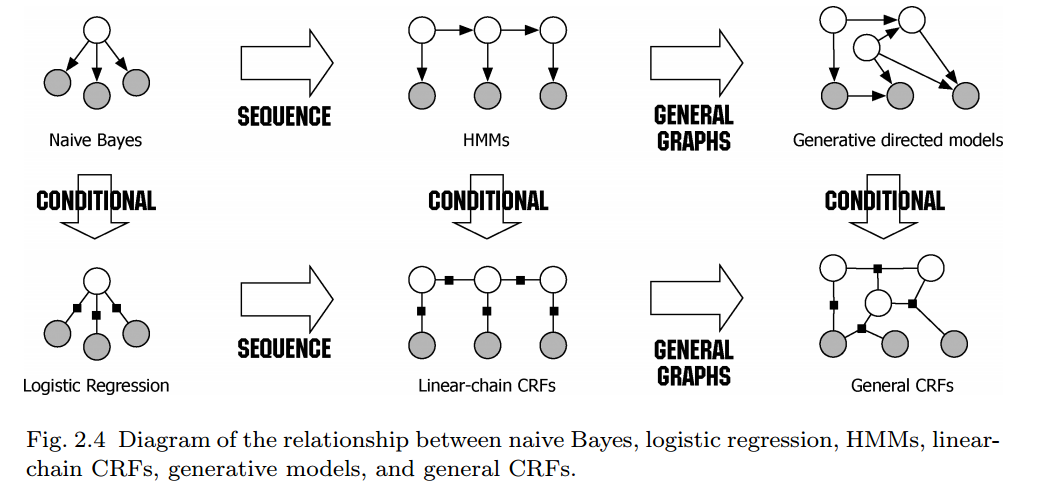
从图中我们可以看出模型之间的演化过程以及模型之间的区别，对于用在分类问题中的逻辑回归与CRF其实都同属于对数线性模型，这里直观的我们也很好理解，当用CRF模型对\(X\)和\(Y\)序列建模时，我们需要判断\(x_i\)对应的标签\(y_i\)时其实可以看做一次逻辑回归分类问题，只不过这个分类问题考虑了上下文的序列信息，也就是说单纯的回归分类会损失上下文的序列信息如：有一系列连续拍摄的照片，现在想在照片上打上表示照片里的活动内容的标记，当然可以将每张照片单独做分类，但是会损失信息，例如当有一张照片上是一张嘴，应该分类到“吃饭”还是分类到“唱K”呢？如果这张照片的上一张照片内容是吃饭或者做饭，那么这张照片表示“吃饭”的可能性就大一些，如果上一张照片的内容是跳舞，那这张照片就更有可能在讲唱K的事情。

设有联合概率分布\(P(Y)\)，由无向图\(G=(V,E)\)表示，在图\(G\)中，结点表示随机变量，边表示随机变量之间的依赖关系，如果联合概率分布\(P(Y)\)满足成对、局部或全局马尔可夫性，就称此联合概率分布为马尔可夫随机场（Markov random filed）也称概率无向图模型（probablistic undirected graphical model）：

• 成对马尔可夫性：设\(u,v\)是无向图\(G\)中任意两个没有边连接的结点，其他所有结点表示为\(O\)，对应的随机变量分别用\(Y_u,Y_v,Y_O\)表示，成对马尔可夫性是指给定随机变量组\(Y_O\)的条件下随机变量\(Y_u,Y_v\)是条件独立的，如下：\[P(Y_u,Y_v|Y_O)=P(Y_u|Y_O)P(Y_v|Y_O)\]
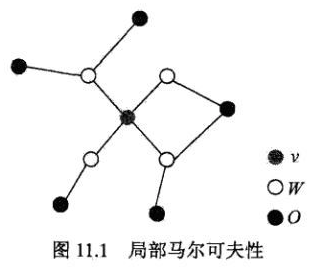
• 局部马尔可夫性：设\(v\in V\)是\(G\)中任意一个节点，\(W\)是与\(v\)有边连接的所有节点，\(O\)是\(v\)，\(W\)以外的其他所有节点。\(v\)表示的随机变量是\(Y_v\)，\(W\)表示的随机变量是\(Y_w\)，\(O\)表示的随机变量是\(Y_o\)。局部马尔可夫性是在给定随机变量组\(Y_w\)的条件下随机变量\(Y_v\)与随机变量\(Y_o\)是独立的。\[P(Y_v,Y_O|Y_W)=P(Y_v|Y_w)P(Y_O|Y_W)\]
  
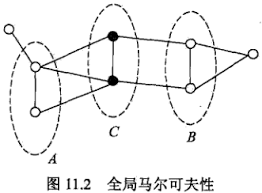
• 全局马尔可夫性：\(A,B\)是\(G\)中被C分开的任意节点集合。全局马尔科夫性是指给定\(Y_c\)条件下\(Y_A\)和\(Y_B\)是条件独立的，即\[P(Y_A,Y_B|Y_C)=P(Y_A|Y_C)P(Y_B|Y_C)\]
  

下面我们具体阐述下一种特殊也常用的线性链条件随机场。

线性链条件随机场

给定一个线性链条件随机场\(P(Y|X)\)，当观测序列为\(x=x_1x_2...\)时，状态序列为 \(y=y_1y_2...\)的概率可写为（实际上应该写为\(P(Y=y|x;θ)\)，参数被省略了）

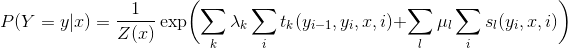
\(Z(x)\)作为规范化因子，是对\(y\)的所有可能取值求和。我们可以用下图来理解：

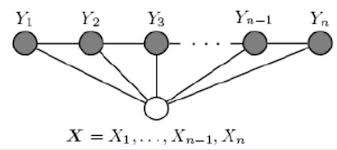
对于线性链CRF，特征函数是个非常重要的概念（很容易联想到HMM的转移概率和发射概率）：

• 转移特征\(t_k(y_{i−1},y_i,x,i)\)是定义在边上的特征函数（transition），依赖于当前位置\(i\)和前一位置\(i-1\)；对应的权值为\(λ_k\)。
• 状态特征\(s_l(y_i,x,i)\)是定义在节点上的特征函数（state），依赖于当前位置\(i\)；对应的权值为\(μ_l\)。

一般来说，特征函数的取值为 1 或 0 ，当满足规定好的特征条件时取值为 1 ，否则为 0 。

简化形式

对于转移特征这一项：

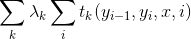
可以看出外面那个求和号是套着里面的求和号的，这种双重求和就表明了对于同一个特征\(k\)，在各个位置\(i\)上都有定义。
基于此，很直觉的想法就是把同一个特征在各个位置\(i\)求和，形成一个全局的特征函数，也就是说让里面那一层求和号消失。在此之前，为了把加号的两项合并成一项，首先将各个特征函数\(t\)（设其共有\(K_1\)个）、\(s\)（设共\(K_2\)个）都换成统一的记号\(f\) ：

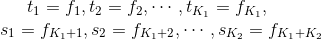
相应的权重同理：

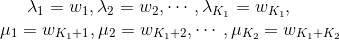
那么就可以记为：

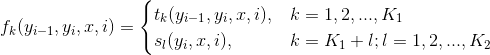
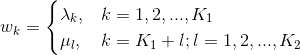
然后就可以把特征在各个位置\(i\)求和，即

其中\(K=K_1+K_2\)。进而可以得到简化表示形式：

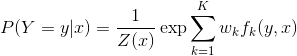
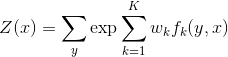
这个形式我们在下一节介绍CRF分词的时候会使用。

CRF分词

对于一个句子的分词问题我们在前面的系列博文中已经阐述，输入的句子\(S\)相当于序列\(X\)，输出的标签序列L相当于序列\(Y\)，我们要训练一个模型，使得在给定\(S\)的前提下，找到其最优对应的\(L\)。
训练该模型的关键点就是特征函数\(F\)的选取以及每个特征函数权重\(W\)的确定，而对于每个特征函数而言，其输入有如下四个要素：

• 句子\(S\)（就是我们要标注词性的句子）
• \(i\)，用来表示句子\(S\)中第\(i\)个单词
• \(l_i\)，表示要评分的标注序列给第i个单词标注的词性
• \(l_{i-1}\)，表示要评分的标注序列给第\(i-1\)个单词标注的词性

它的输出值是0或者1,0表示要评分的标注序列不符合这个特征，1表示要评分的标注序列符合这个特征。我们发现这里的特征函数在选取当前\(s_i\)的对应标签\(l_i\)时，只考虑了其前一个标签\(l_{i-1}\)，这就是使用了我们上一节阐述的线性链条件随机场，而公式中的f就是我们这里的特征函数。
Note：在实际的应用时，除了单一的特征选取，我们通常会通过构造复合特征的方式，考虑更多的上下文信息。

CRF VS HMM

在上一篇博文中我们介绍了HMM在分词中的使用，那么读者肯定会问既然HMM已经能完成任务，为什么还需要CRF来重新搞一波，原因就是CRF比HMM更强大。
对于序列\(L\)和\(S\)，根据之前的介绍我们易知如下公式：

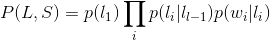
其中\(w_i\)为\(S\)中第\(i\)个词，\(l_i\)为第\(i\)个词的标签，公式中前半部分为状态转移概率，后半部分为发射概率。我们用对数形式表示该式：

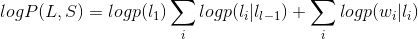
把这个式子与CRF的简化形式比较，不难发现，如果我们把第一个HMM式子中的log形式的概率看做是第二个CRF式子中的特征函数的权重的话，我们会发现，CRF和HMM具有相同的形式。所以可以说：每一个HMM模型都等价于某个CRF。
总结下两者的区别：

• HMM是生成模型以联合概率建模，CRF是判别模型以条件概率建模
• HMM为了简化计算做了有限状态假设和一对一假设（当前的单词只依赖于当前的标签，当前的标签只依赖于前一个标签），所以在特征选取上会有很多限制；而CRF可以定义数量更多，种类更丰富的特征函数（如定义一个特征函数f，考虑当前词离句首的距离，来着眼于整个句子）。
• CRF可以使用任意的权重 将对数HMM模型看做CRF时，特征函数的权重由于是log形式的概率，所以都是小于等于0的，而且概率还要满足相应的限制，但在CRF中，每个特征函数的权重可以是任意值，没有这些限制。

Note:其实在HMM和CRF之间还有一个MEMM，即最大熵马尔科夫模型，MEMM模型是对转移概率和表现概率建立联合概率，统计时统计的是条件概率，但MEMM容易陷入局部最优，是因为MEMM只在局部做归一化（标记偏置问题），不过一般用的不多我们就不过多介绍，可参考[5]

代码实现

下面我们利用wapiti来实现一个简单的CRF分词器。相关说明：

• wapiti是一个开源的CRF工具，doc在这里：https://wapiti.limsi.fr/
• 数据源来源于msr整理所得：http://sighan.cs.uchicago.edu/bakeoff2005/
• python
• ubuntu/macos

训练代码

https://github.com/xlturing/machine-learning-journey/tree/master/seg_crf
大家可以直接看下源代码

实验结果

• Load model
• Label sequences
  1000 sequences labeled 3.96%/43.30%
  2000 sequences labeled 3.89%/44.00%
  3000 sequences labeled 3.87%/44.50%
  Nb sequences : 3985
  Token error : 3.85%
  Sequence error: 44.74%
• Per label statistics
  B Pr=0.96 Rc=0.98 F1=0.97
  E Pr=0.96 Rc=0.98 F1=0.97
  S Pr=0.97 Rc=0.95 F1=0.96
  M Pr=0.92 Rc=0.87 F1=0.90
• Done

这个训练集和测试集都相对较小，效果还不错，读者在真正上线使用时还需要依赖词典等诸多与场景对应的分词特性，本文更加关注原理和理解。

参考文献

1. HMM MEMM CRF 区别 联系
2. 如何轻松愉快地理解条件随机场（CRF）？
3. NLP —— 图模型（二）条件随机场（Conditional random field，CRF）
4. An Introduction to Conditional Random Fields
5. HMM MEMM CRF 区别 联系
6. 《统计学习方法》 李航