图->遍历
文字描述
从图中某一顶点出发遍历图中其余顶点,且使每一个顶点仅被访问一次,这一过程就叫图的遍历。
深度优先搜索:类似树的先根遍历;假设初始状态下,图中所有顶点都未曾被访问,则从某个顶点出发,访问此顶点,然后依次从v的未被访问的邻接点出发继续深度优先遍历图,直到图中所有和v有路径相通的顶点都被访问到;若此时图中尚有顶点未被访问,则另选一个未曾被访问的顶点作起始点。
广度优先搜索:类似数的层次遍历;以v为起始点,由近及远,依次访问和v有路径相通且路径长度为1,2,…的顶点。
示意图

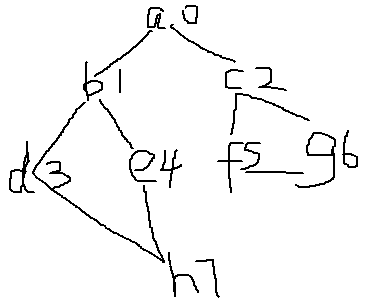
算法分析
深度优先搜索:遍历图的过程实质上是对每个顶点找其邻接点的过程。其耗费的时间取决于所采用的存储结构。当用二维数组表示邻接矩阵作图的存储结构时,查找每个顶点的邻接点所需时间为n*n, 其中n为图中顶点数。而当以邻接表作图的存储结构时,找邻接点所需时间为e,其中e为无向图中的边数或有向图中弧的数。由此,当以邻接表作存储结构时,深度优先搜索遍历图的时间复杂度为n+e。
广度优先搜索:其时间复杂度和深度优先遍历相同,两者不同之处在于对顶点的访问顺序不同。
代码实现
/*
1.以邻接表作为图的存储结构创建图。
2.用深度优先搜索的方法对图中结点进行遍历
3.用广度优先搜索的方法对图中结点进行遍历
*/ #include <stdio.h>
#include <stdlib.h>
#include <string.h> #define INFINITY 100000 //最大值
#define MAX_VERTEX_NUM 20 //最大顶点数
#define None -1
typedef enum {DG, DN, UDG, UDN} GraphKind; //{有向图,有向网,无向图,无向网}
typedef char VertexType;
typedef struct{
char note[];
}InfoType;
//与顶点相连的弧结点
typedef struct ArcNode{
int adjvex; //该弧所指向的顶点的位置
struct ArcNode *nextarc; //指向下一条弧的指针
InfoType *info; //该弧相关信息的指针
}ArcNode;
//顶点结点
typedef struct VNode{
VertexType data;//顶点信息
ArcNode *firstarc;//指向第一条依附该顶点的弧的指针
}VNode, AdjList[MAX_VERTEX_NUM];
//图结点
typedef struct{
AdjList vertices;
int vexnum;//图的顶点数
int arcnum;//图的弧数
int kind; //图的种类标志
}ALGraph; /*
若G中存在顶点u,则返回该顶点在图中位置;否则返回-1。
*/
int LocateVex(ALGraph G, VertexType v)
{
int i = ;
for(i=; i<G.vexnum; i++){
if(G.vertices[i].data == v){
return i;
}
}
return -;
} /*
在链表L的头部前插入v
*/
int InsFirst(ArcNode *L, int v)
{
ArcNode *n = (ArcNode *)malloc(sizeof(struct ArcNode));
n->adjvex = v;
n->nextarc = L->nextarc;
L->nextarc = n;
return ;
} /*
采用邻接表的存储结构,构造无向图
*/
int CreateUDG(ALGraph *G)
{
int i = , j = , k = , IncInfo = ;
int v1 = , v2 = ;
char tmp[] = {}; printf("输入顶点数,弧数,其他信息标志位: ");
scanf("%d,%d,%d", &G->vexnum, &G->arcnum, &IncInfo); for(i=; i<G->vexnum; i++){
printf("输入第%d个顶点: ", i+);
memset(tmp, , sizeof(tmp));
scanf("%s", tmp);
G->vertices[i].data = tmp[];
G->vertices[i].firstarc = malloc(sizeof(struct ArcNode));
G->vertices[i].firstarc->adjvex = None;
G->vertices[i].firstarc->nextarc = NULL;
} for(k=; k<G->arcnum; k++){
printf("输入第%d条弧(顶点1, 顶点2): ", k+);
memset(tmp, , sizeof(tmp));
scanf("%s", tmp);
sscanf(tmp, "%c,%c", &v1, &v2);
i = LocateVex(*G, v1);
j = LocateVex(*G, v2);
InsFirst(G->vertices[i].firstarc, j);
InsFirst(G->vertices[j].firstarc, i);
if(IncInfo){
//other info on arc
}
}
return ;
} /*
采用邻接表的存储结构,构造图
*/
int CreateGraph(ALGraph *G)
{
printf("输入图类型: -有向图(0), -有向网(1), +无向图(2), -无向网(3): ");
scanf("%d", &G->kind);
switch(G->kind){
case DG:
case DN:
case UDN:
printf("还不支持!\n");
return -;
case UDG:
return CreateUDG(G);
default:
return -;
}
} /*
输出图的信息
*/
void printG(ALGraph G)
{
if(G.kind == DG){
printf("类型:有向图;顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
}else if(G.kind == DN){
printf("类型:有向网;顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
}else if(G.kind == UDG){
printf("类型:无向图;顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
}else if(G.kind == UDN){
printf("类型:无向网;顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
}
int i = ;
ArcNode *p = NULL;
for(i=; i<G.vexnum; i++){
printf("%c\t", G.vertices[i].data);
p = G.vertices[i].firstarc;
while(p){
if(p->adjvex != None)
printf("%d\t", p->adjvex);
p = p->nextarc;
}
printf("\n");
}
return;
} //////////////////////////////////////////////////////////////////////
//////////////////////////////////////////////////////////////////////
//////////////////////////////////////////////////////////////////////
//////////////////////////////////////////////////////////////////////
//开始用深度优先搜索的方法对图中结点进行遍历
int Visited[MAX_VERTEX_NUM] = {};//访问标志数组
void (*VisitFun)(ALGraph G, int v);//函数变量 //打印顶点中位置v的顶点信息
void printfun(ALGraph G, int v){
printf("[%d]:%c\t", v, G.vertices[v].data);
} //返回图G中与顶点位置为v的顶点相连的第一个结点在顶点中的位置
int FirstAdjVex(ALGraph G, int v)
{
return G.vertices[v].firstarc->nextarc->adjvex;
} //返回图G中与顶点位置为v的顶点相连的结点w的下一个结点在顶点中的位置
int NextAdjVex(ALGraph G, int v, int w)
{
ArcNode *arc = G.vertices[v].firstarc;
while(arc && arc->adjvex != w){
arc = arc->nextarc;
}
if(arc && arc->nextarc){
return arc->nextarc->adjvex;
}
return -;
} //从第v个顶点出发递归地深度优先遍历图G
void DFS(ALGraph G, int v){
//访问第v个顶点
Visited[v] = ;
VisitFun(G, v);
int w = ;
for(w=FirstAdjVex(G,v); w>=; w=NextAdjVex(G,v,w)){
//对v的尚未访问的邻接顶点w递归调用DFS
if(!Visited[w]){
DFS(G,w);
}
}
} //对图G作深度优先遍历
void DFSTraverse(ALGraph G, void (*Visit)(ALGraph G, int v))
{
printf("深度优先搜索: ");
//使用全局变量VisitFun, 是DFS不必设函数指针参数
VisitFun = Visit;
int v = ;
//访问标志数组初始化
for(v=; v<G.vexnum; v++){
Visited[v] = ;
}
for(v=; v<G.vexnum; v++){
//对尚未访问的顶点调用DFS
if(!Visited[v])
DFS(G, v);
}
} //////////////////////////////////////////////////////////////////////
//////////////////////////////////////////////////////////////////////
//////////////////////////////////////////////////////////////////////
//////////////////////////////////////////////////////////////////////
//开始用广度优先搜索的方法对图中结点进行遍历
typedef struct QNode{
int data;
struct QNode *next;
}QNode, *QuenePtr; typedef struct{
QuenePtr front;
QuenePtr rear;
}LinkQueue;
LinkQueue *InitQueue(void){
LinkQueue *Q = (LinkQueue*)malloc(sizeof(LinkQueue));
Q->front = Q->rear = (QuenePtr)malloc(sizeof(QNode));
Q->front->next = Q->rear->next = NULL;
return Q;
}
int QueueEmpty(LinkQueue *Q){
if(Q->front == Q->rear){
return ;
}else{
return -;
}
}
int EnQueue(LinkQueue *Q, int e){
QuenePtr p = (QuenePtr)malloc(sizeof(QNode));
p->data = e;
p->next = NULL;
Q->rear->next = p;
Q->rear = p;
return ;
} int DeQueue(LinkQueue *Q, int *e)
{
if(Q->rear == Q->front){
return -;
}
QuenePtr p = Q->front->next;
*e = p->data;
Q->front->next = p->next;
if(p == Q->rear){
Q->rear = Q->front;
}
free(p);
return ;
} void PrintQ(LinkQueue *Q)
{
QuenePtr head = Q->front;
while(head){
printf("%d\t", head->data);
head = head->next;
}
printf("\n");
} /*广度优先搜索
*按广度优先非递归遍历图G。使用辅助队列Q和访问标志数组Visited
*/
void BFSTraverse(ALGraph G, void (*Visit)(ALGraph G, int v))
{
printf("广度优先搜索: ");
int v = ;
int u = ;
int w = ;
//访问标志数组初始化
for(v=; v<G.vexnum; v++){
Visited[v] = ;
}
//置空的辅助队列Q
LinkQueue *Q = InitQueue();
for(v=; v<G.vexnum; v++){
if(!Visited[v]){
//v尚未访问
Visited[v] = ;
//访问v顶点
Visit(G, v);
//v入队列
EnQueue(Q, v); while(QueueEmpty(Q)){
//队头元素出队并置为u
DeQueue(Q, &u);
for(w=FirstAdjVex(G, u); w>=; w=NextAdjVex(G, u, w)){
if(!Visited[w]){
//w为u的尚未访问的邻接顶点
Visited[w] = ;
Visit(G, w);
EnQueue(Q, w);
}
}
}
}
}
} int main(int argc, char *argv[])
{
ALGraph G;
if(CreateGraph(&G) > -){
printG(G);
}
DFSTraverse(G, printfun);printf("\n");
BFSTraverse(G, printfun);printf("\n");
return ;
}
图深度优先遍历和广度优先遍历
代码运行
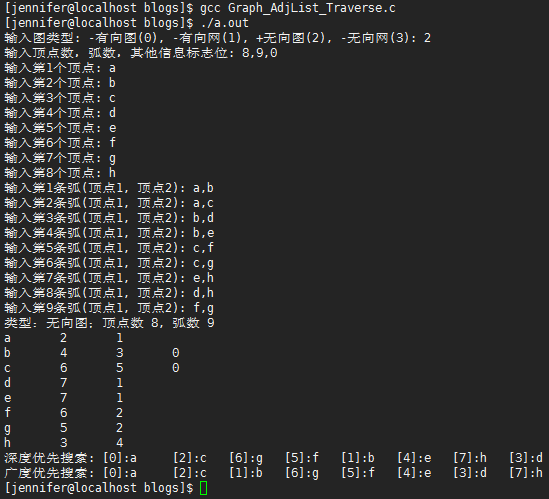
图->遍历的更多相关文章
- DS图遍历--深度优先搜索
DS图遍历--深度优先搜索 题目描述 给出一个图的邻接矩阵,对图进行深度优先搜索,从顶点0开始 注意:图n个顶点编号从0到n-1 代码框架如下: 输入 第一行输入t,表示有t个测试实例 第二行输入n, ...
- Gremlin:图遍历语言
Gremlin简介 Gremlin是Apache TinkerPop 框架下的图遍历语言.Gremlin是一种函数式数据流语言,可以使得用户使用简洁的方式表述复杂的属性图(property graph ...
- 一步一步学数据结构之n--n(图遍历--深度优先遍历--非递归实现)
前面已经说了图的深度优先遍历算法,是用递归实现的,而在这里就讲一下用非递归实现,需要借助栈: 算法思想: 1. 栈初始化 2. 输出起始顶点,起始顶点改为“已访问”标志,将 ...
- PAT A1134 Vertex Cover (25 分)——图遍历
A vertex cover of a graph is a set of vertices such that each edge of the graph is incident to at le ...
- PAT A1034 Head of a Gang (30 分)——图遍历DFS,字符串和数字的对应保存
One way that the police finds the head of a gang is to check people's phone calls. If there is a pho ...
- PAT A1013 Battle Over Cities (25 分)——图遍历,联通块个数
It is vitally important to have all the cities connected by highways in a war. If a city is occupied ...
- 算法学习笔记(六) 二叉树和图遍历—深搜 DFS 与广搜 BFS
图的深搜与广搜 复习下二叉树.图的深搜与广搜. 从图的遍历说起.图的遍历方法有两种:深度优先遍历(Depth First Search), 广度优先遍历(Breadth First Search),其 ...
- ent 基本使用十五 一个图遍历的例子
以下是来自官方的一个user group pet 的查询demo 参考关系图 环境准备 docker-compose mysql 环境 version: "3" services: ...
- DS图遍历--广度优先搜索
题目描述 代码框架如下: 输入 第一行输入t,表示有t个测试实例 第二行输入n,表示第1个图有n个结点 第三行起,每行输入邻接矩阵的一行,以此类推输入n行 第i个结点与其他结点如果相连则为1,无连接则 ...
随机推荐
- JVM 内部原理(五)— 基本概念之 Java 虚拟机官方规范文档,第 7 版
JVM 内部原理(五)- 基本概念之 Java 虚拟机官方规范文档,第 7 版 介绍 版本:Java SE 7 每位使用 Java 的程序员都知道 Java 字节码在 Java 运行时(JRE - J ...
- java 注解默认值
package com.zejian.annotationdemo; import java.lang.annotation.ElementType; import java.lang.annotat ...
- 面试Spring之bean的生命周期
找工作的时候有些人会被问道Spring中Bean的生命周期,其实也就是考察一下对Spring是否熟悉,工作中很少用到其中的内容,那我们简单看一下. 在说明前可以思考一下Servlet的生命周期:实例化 ...
- python利用lxml读写xml格式文件
之前在转换数据集格式的时候需要将json转换到xml文件,用lxml包进行操作非常方便. 1. 写xml文件 a) 用etree和objectify from lxml import etree, o ...
- 部门sonarque代码扫描测试服务器docker化
部门内部的服务器太多了,打算将对应的测试环境docker化. 转成docker后,以后不管是升级调研还是定制化开发测试都方便,就是事情太多,一直没有抽出身来做,今天处理下并把过程记录下来跟大家分享下. ...
- springboot集成rabbitmq的一些坑
一.默认管理页面地址是 http://127.0.0.1:15672 但是spring配置连接里面要把端口改成5672,如果不配置的话默认就是端口5672 spring.rabbitmq.host=1 ...
- thinkphp 无限极 评论
郑创 今天用啦一天的时间用了各种方法终于把评论成无限极了,随便评论,有判断自己不能评论自己,下面先说前台源代码! 要实现的视图 前台源代码html模板 <div class="wen_ ...
- http://202.194.116.8/webapps/portal/frameset.jsp?tab_id=_2_1&url=%2fwebapps%2fblackboard%2fexecute%2
http://202.194.116.8/webapps/portal/frameset.jsp?tab_id=_2_1&url=%2fwebapps%2fblackboard%2fexecu ...
- asp:LinkBtton PostBackUrl 中文乱码
这个也不行: HttpUtility.UrlEncode("中文") 替代方案为:<asp:HyperLink NavigateUrl=“~/路径” Target=" ...
- 洛谷 P1181数列分段SectionI 【贪心】
题目描述 对于给定的一个长度为NN的正整数数列A_iAi,现要将其分成连续的若干段,并且每段和不超过MM(可以等于MM),问最少能将其分成多少段使得满足要求. 输入输出格式 输入格式: 第1行包含两 ...
