生成更大的陆地 Making A Large Island

2018-10-06 19:44:18

问题描述：

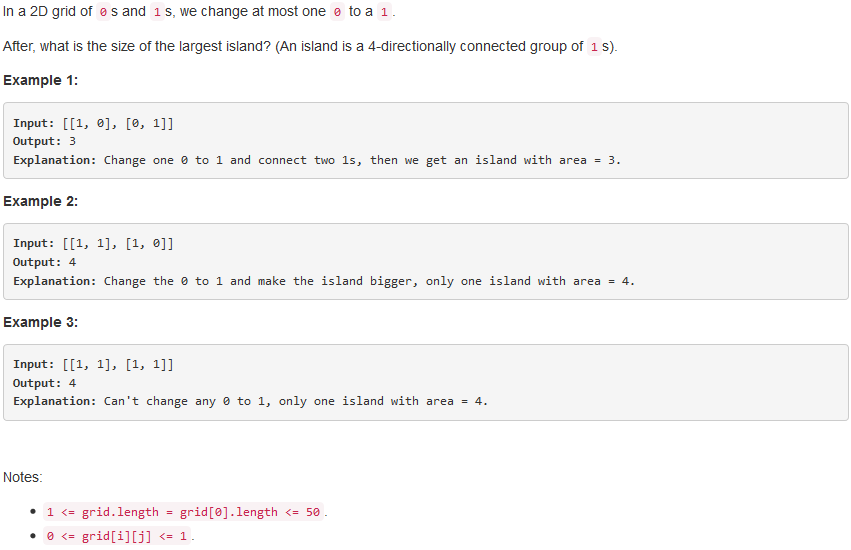
问题求解：

经典的求连通块问题的扩展，问题规模不大，可以暴力求解。

解法一、Brute Force O(n^4)

    int[][] dirs = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};

    public int largestIsland(int[][] grid) {
        int res = Integer.MIN_VALUE;
        int n =  grid.length;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1) res = Math.max(res, helper(grid, i, j, new int[n][n]));
                else {
                    grid[i][j] = 1;
                    res = Math.max(res, helper(grid, i, j, new int[n][n]));
                    grid[i][j] = 0;
                }
            }
        }
        return res;
    }

    private int helper(int[][] grid, int x, int y, int[][] used) {
        int n = grid.length;
        int res = 1;
        used[x][y] = 1;
        for (int[] dir : dirs) {
            int px = x + dir[0];
            int py = y + dir[1];
            if (px < 0 || px >= n || py < 0 || py >= n || used[px][py] == 1 || grid[px][py] == 0) continue;
            res += helper(grid, px, py, used);
        }
        return res;
    }

解法二、

为每个连通块做上标记，并得到每个连通块的面积，之后再对0进行遍历，依次寻找其四个相邻的边的area，将他们加起来再从中取max。算法总的时间复杂度为O(n ^ 2)。

    public int largestIsland(int[][] grid) {
        int res = Integer.MIN_VALUE;
        int n =  grid.length;
        Map<Integer, Integer> map = new HashMap<>();
        int color = 0;
        int area = 0;
        map.put(color++, area);
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1) area = dfs(grid, i, j, ++color);
                map.put(color, area);
                res = Math.max(res, area);
            }
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 0) {
                    int curArea = 1;
                    Set<Integer> set = new HashSet<>();
                    set.add(getColor(grid, i - 1, j));
                    set.add(getColor(grid, i + 1, j));
                    set.add(getColor(grid, i, j + 1));
                    set.add(getColor(grid, i, j - 1));
                    for (int c : set) {
                        curArea += map.get(c);
                    }
                    res = Math.max(res, curArea);
                }
            }
        }
        return res;
    }

    private int getColor(int[][] grid, int x, int y) {
        if (x < 0 || x >= grid.length || y < 0 || y >= grid.length) return 0;
        else return grid[x][y];
    }

    private int dfs(int[][] grid, int x, int y, int color) {
        if (x < 0 || x >= grid.length || y < 0 || y >= grid.length || grid[x][y] != 1) return 0;
        grid[x][y] = color;
        return 1 + dfs(grid, x + 1, y, color) + dfs(grid, x - 1, y, color) +
                dfs(grid, x, y - 1, color) + dfs(grid, x, y + 1, color);
    }