Reshape以及向量机分类学习和等高线绘制代码

　　首先科普一下python里面对于数组的处理，就是如果获取数组大小，以及数组元素数量，这个概念是不一样的，就是一个size和len处理不用。老规矩，上代码：

 arr2 = np.array([-19.51679711, -18.06166131, -16.65282549, 8.70287809,9.9485567 , 11.23867649, 3,4])
 pprint(arr2.size)
 pprint(len(arr2))

>>8

>>8

　　貌似两者没啥区别，但是真的是这样吗？

Code:

 arr2 = np.array([[-19.51679711, -18.06166131, -16.65282549, 8.70287809,9.9485567 , 11.23867649, 3,4]])
 pprint(arr2.size)
 pprint(len(arr2))

>>8

>>1

　　在多维数组中，size代表的是所有的最小单元的总和，len则是代表多维数组元素的数量。

　　接着我们讲一下reshape，重新塑形，简单的讲就是将一个一维数组，打成多维数组：

 arr = np.arange(6)
 brr = arr.reshape((3,2))
 pprint(brr)

>> array([[0, 1], [2, 3], [4, 5]])

　　介绍完了基础知识，我们再来看一下SVM的分类学习

 from sklearn.datasets import make_moons
 X, y = make_moons(n_samples=100, noise=0.15, random_state=42)

 def plot_dataset(X, y, axes):
     plt.plot(X[y==0, 0], X[y==0, 1], "bs")
     plt.plot(X[y==1, 0], X[y==1, 1], "g^")
     plt.axis(axes)
     plt.grid(True, which="both") #这个双引号行吗？没问题
     plt.xlabel("$x_1$")
     plt.ylabel("$x_2$")

 plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
 plt.show()

 from sklearn.pipeline import Pipeline
 from sklearn.preprocessing import PolynomialFeatures

 polynomial_svm_clf=Pipeline((
     ("ploy_feature", PolynomialFeatures(degree=3)), # 这里为什么需要多项式？有什么影响？
     ("ploy_scale", StandardScaler()), # 缩小，减小离群点对于整体影响；
     ("svm", LinearSVC(C=10, loss="hinge"))
 ))

 polynomial_svm_clf.fit(X, y)

 # 基于坐标范围，形成点群（X）以及每个点的分类（y，等高线就是根据y值绘制的）；所以可以看到每个点其实是有三个属性，坐标（x, y）以及分类
 # 这个函数就是要生成这样的点，然后根据分类绘制等高线，这批套路非常重要
 def plot_prediction(clf, axes):
     x0s = np.linspace(axes[0], axes[1], 100) # 根据坐标范围等分点
     x1s = np.linspace(axes[2], axes[3], 100)
     # 这个是做什么的？ meshgrid之后将会形成两套矩阵, 有大量容易，其实都是根据第一行（x0)）和第一列（x1）进行衍生
     x0, x1 = np.meshgrid(x0s, x1s)
     # 这个又是在做什么？将衍生的矩阵里面的向量进行拉伸，通过np.c_进行整合，将会得到一个矩阵，矩阵里面每个向量都是两个元素（代表一个坐标），
     # 来自于拉伸的两个矩阵的组合
     X = np.c_[x0.ravel(), x1.ravel()]
     plt.plot(X[501:600,0], X[501:600,1], "ys") # 这是我写的一段测试代码，打印出来的是X的部分点集，这里注意多维数组[:,:]中第一个参数代表行范围，第二个参数代表列范围
     # 获取的完了predict为什么要reshape一下？clf.predict(X)返回的只是一个一维数组，每个数组对应X的一个向量（每个向量都是一个点），
     # reshape之后，将会复制N行并返回N行的矩阵（N的值和X的行向量数量是一样的）
     y_pred = clf.predict(X).reshape(x0.shape)
     # decsion_function干嘛，为啥完事后有reshape一下？decision_function代表参数实例（各个元素）到分类平面（超平面）的距离，所以其数量
     # 是等于X中向量的数量：10000，x0.shape是（100,100），于是reshape之后将会成为100行100列的多维数组
     y_decision = clf.decision_function(X).reshape(x0.shape)
     # 绘制分类（等高）线
     plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
     # 绘制距离线
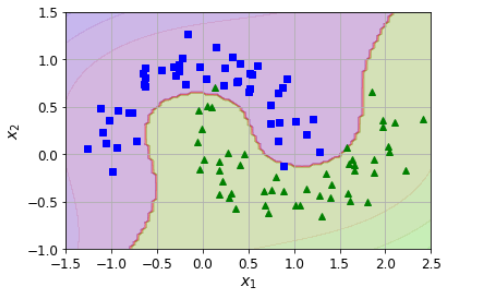
     plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)

 plot_prediction(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5]) #花了两条等高线
 plot_dataset(X, y, [-1.5, 2.5, -1, 1.5]) # 换了两个交互的半环
 plt.show()

　　这段代码基本思路如下：

　　我先有数据，一个月牙环形数据（左侧图）；然后我用这个数据，训练出来一个向量机（SVM），因为数据是曲线的，所以需要高次公式，于是搞了一个Pipeline，整合了Scalar和SVM来进行学习；通过fit函数，把模型的参数都搞掂了；然后我利用这个向量机来进行绘制边界线，怎么来绘制呢？首先在坐标中获取10000个点，均匀的散播在整个坐标系中；我再把这些点扔到SVM中，让他根据之前学习的结果获取分类，contours英文意思就是轮廓，在matlibplot中，contourf这个函数将会把轮廓画出来，并且填充颜色；简单讲就是同类别同颜色，然后会在不同类别之间画出一条分界线。

　　这段代码意义在于讲清楚了SVM的学习能力；通过针对半月环形数据的学习掌握了参数，具备了对于点判断分类的能力；未来当有海量的数据需要判断的时候，会基于之前的学习模型，来进行判断，分类，在右图海量数据作为测试数据的场景下，通过轮廓线说明了SVM所具备的学习能力。