深度学习Bible学习笔记:第六章 深度前馈网络
第四章 数值计算(numerical calculation)和第五章 机器学习基础下去自己看。
一、深度前馈网络(Deep Feedfarward Network,DFN)概要:
DFN:深度前馈网络,或前馈神经网络(FFN)/多层感知机(MLP)
目标:近似模拟某函数f y=f(x;θ)
学习参数θ的值,得到最佳的函数近似。
注:并非完美模拟大脑,只是实现统计泛化,函数近似机。源于大脑,但远远比不上大脑
结构: f(x)=f(3)(f(2)(f(1)(x)))
前馈(feedforward):信息一直往下流动,一路向前,不回头。例如:CNN
反馈(feedbackward):前馈的扩展,增加反馈连接,走一段,回头看看。例如:RCNN
线性模型:
优点:简单快速,线性回归和逻辑回归(广义线性回归)
局限性:受限于线性函数,无法表示任意变量间的相互作用
非线性模型(扩展):
套上一层皮:非线性变换
如何选择非线性变换?映射φ
(1)找通用函数:高维,过拟合。
只要函数维度足够高,总能拟合训练集,然而,测试集泛化不佳
非通用函数基于局部光滑原则
(2)人工设计函数:主流,极度依赖专家+领域,难以迁移
(3)自动学习函数:两全其美
同时学习函数参数+权重参数
唯一放弃凸性的方法,利大于弊
通用:只需要一个广泛的函数族,不用太精确
可控:专家知识辅助泛化,只需要找函数族φ(x;θ)
训练一个前馈网络需要做什么?
设计决策同线性模型
优化模型
代价函数
输出单元
网络结构该如何设计?
多少层,连接如何设置,每层多少个单元
如何高效地计算梯度?
反向传播
补充:线性变换
什么是线性变换?
仿射变换:线性变换+平移
具体:缩放、旋转、错切、翻转等
参考:《如何通俗讲解仿射变换》
什么是非线性变换?
参考第二章分享笔记或3Blue 1 Brown的《线性代数本质》
书面定义:加法+数乘——抽象
形象理解:
只需满足两点要求:原点不变,直线还是直线(不能扭曲)
二、如何解决异或问题
XOR函数(“异或”逻辑):两个二进制的运算
注:这道题绝不简单,曾引发AI的第一个寒冬
异或门是神经网络的命门!
解决:非线性变换+BP
人:
简单规则:if。。。else。。。
找规律:x+y=1,怎么自动学习
机器:
确定性、自动化、泛化能力
其他。
线性方法:f(x,w,b)=xTw+b
回归问题
均方误差
结果:任意点都输出0.5,失败。(w=0,以及b=0.5)
为什么会这样?
线性模型中各变量的参数固定
不能通过一个变量改变另外一个变量
结论:
线性模型无法解决异或问题。
那么,怎么办?——空间变换
低维线性不可分,高维线性可分(SVM)
非线性变换实现空间变换
两层神经网络可以无限逼近任意连续函数
网络结构:
两个输入,一个隐含层,一个输出
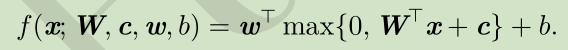
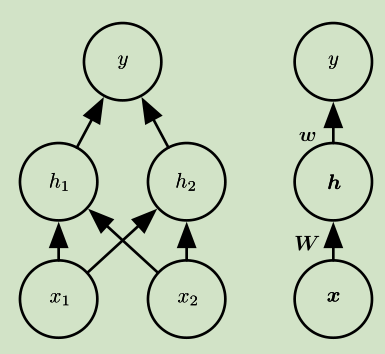
激活函数:
ReLU(整流线性单元)
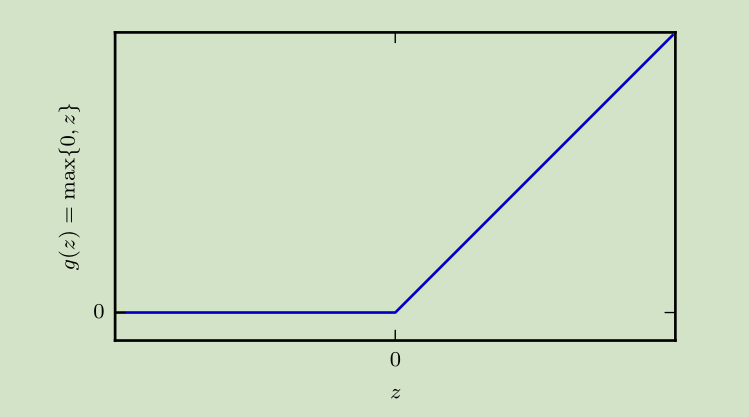
一个解:
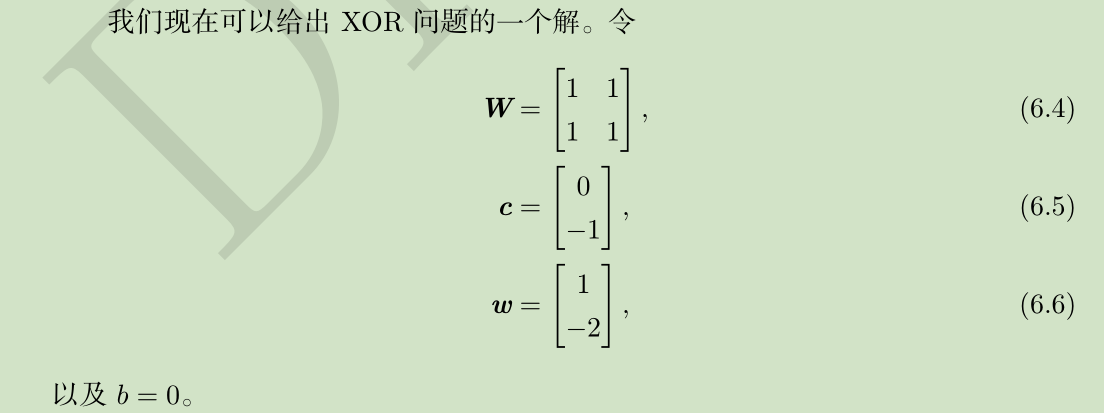
补充:
ReLUc长的是挺简单,可某个点有点膈应,可导吗?——不可导
那为什么还用它?——计算友好,特殊点特殊处理(给0或1),仿生
可导,可微,连续?
连续:有定义、光滑(极限存在)、无间断点。
可微和可导近似等效(多元情形不适用)
可积允许间断点
可导必连续,必可积。反之不可行。
见证奇迹的时刻(睁大眼睛看):
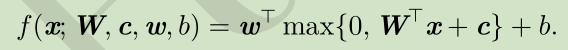
步骤:
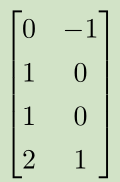
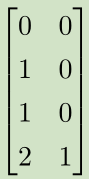
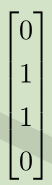
X--->XW--->XW+c--->ReLU--->*w
空间变换:正方形--->直线--->分段直线(线性可分)
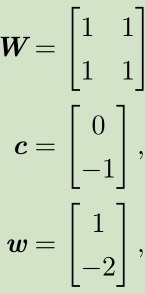 --->
--->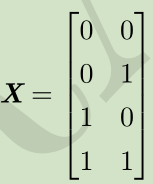 --->
--->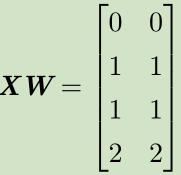 --->
---> --->
---> --->
--->
回想一下:
线性模型无法解决异或问题
低维线性不可分,高维线性可分
多个低级分类器组合成复杂分类器
《A friendly intruduction to Deep Learning and Neural Networks》
形象感知:
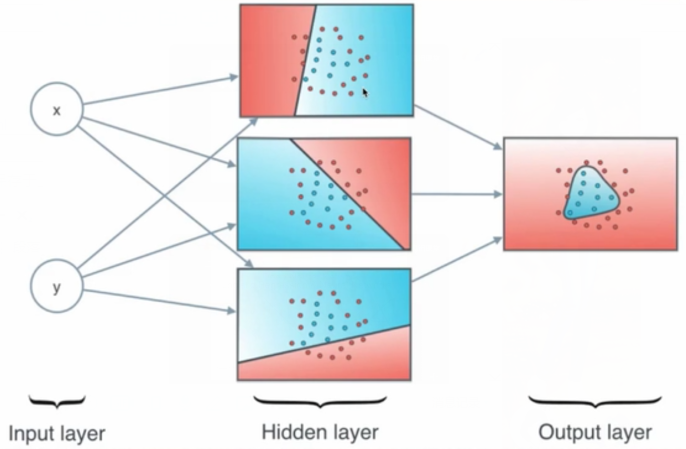
线性边界到非线性边界。
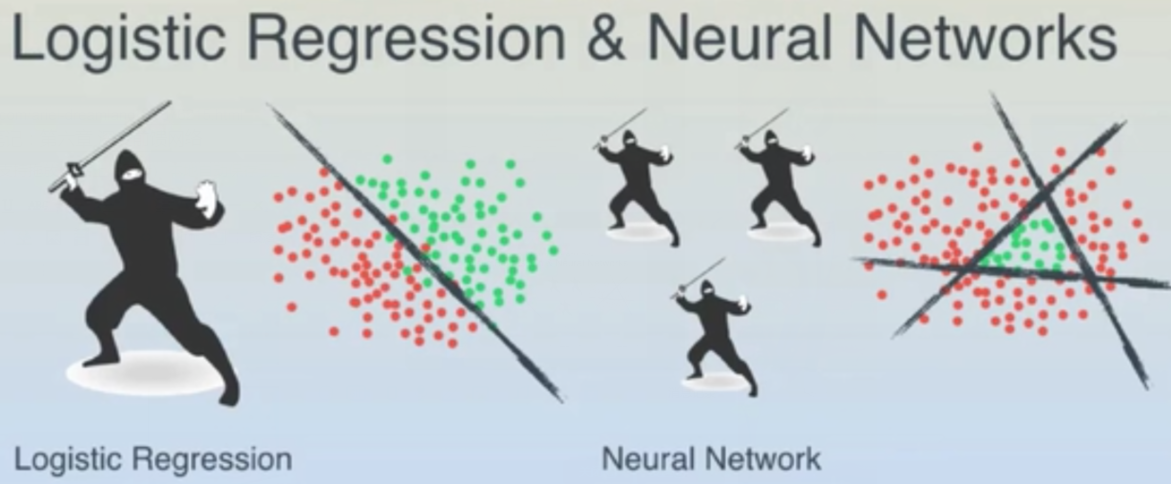
补充:直观感受异或分类
问题:人工求解--->自动训练?
理论证明:两层神经网络可以无限逼近任意连续函数
层数越深,表示能力越强
Google playground(可以下去自己搜索体验一下):
理想--->现实(近似最优解)
三、基于梯度的学习
虽然异或是AI命门,但还只是小儿科
实际情况,训练样本和参数都是数十亿级别
怎么办?——梯度下降
目前为止,神经网络和线性模型都用梯度下降
但最大的区别是:神经网络的非线性导致代价函数非凸,无法收敛到全局最优。
注:凸优化从任何一个初始值触发均能收敛到全局最优
如何计算梯度?
梯度下降升级版+BP算法
梯度下降:
当前位置最陡峭的方向可能最快(局部)
实际问题,高维空间如何收敛?(见第八章讲解)
设计要点:
优化算法:梯度下降
代价函数:交叉熵(负最大似然)

代价函数的梯度必须足够大,并有足够的预测能力,所以不要用sigmoid
贯穿神经网络设计的一个反复出现的主题是代价函数的梯度必须足够的大和具有足够的预测性,来为学习算法提供一个好的指引(见原书page111下)。
代价函数是一个泛函(函数到实数的映射)
如何对泛函求解?变分法


输出单元:线性单元,sigmoid单元,softmax单元等,等多细节请认真看书。
梯度下降对比(好好看书)。
四、反向传播
怎么更新网络权重?传统方法:固定其他变量,只计算一个
反向传播(back propagation):代价函数信息向后流动,以便计算梯度,甚至任意函数的导数
反向传播仅用于计算梯度,并非多层网络的学习方法!
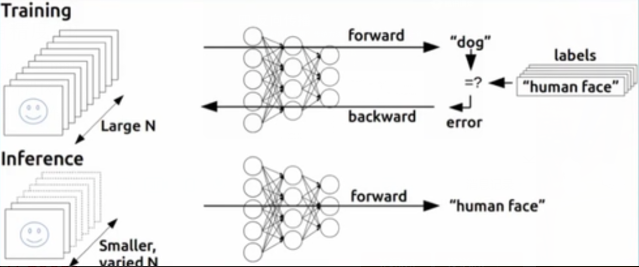
为什么要理解反向传播?TensorFlow工具不是现成的吗?

不要只会用工具,否则神经网络永远都是黑盒!不要在应用网络的时候,出了问题,都不知道怎么调试,学习任何技术,都要了解原理,不要只会使用工具,让自己也变成了单纯的工具。
计算图:
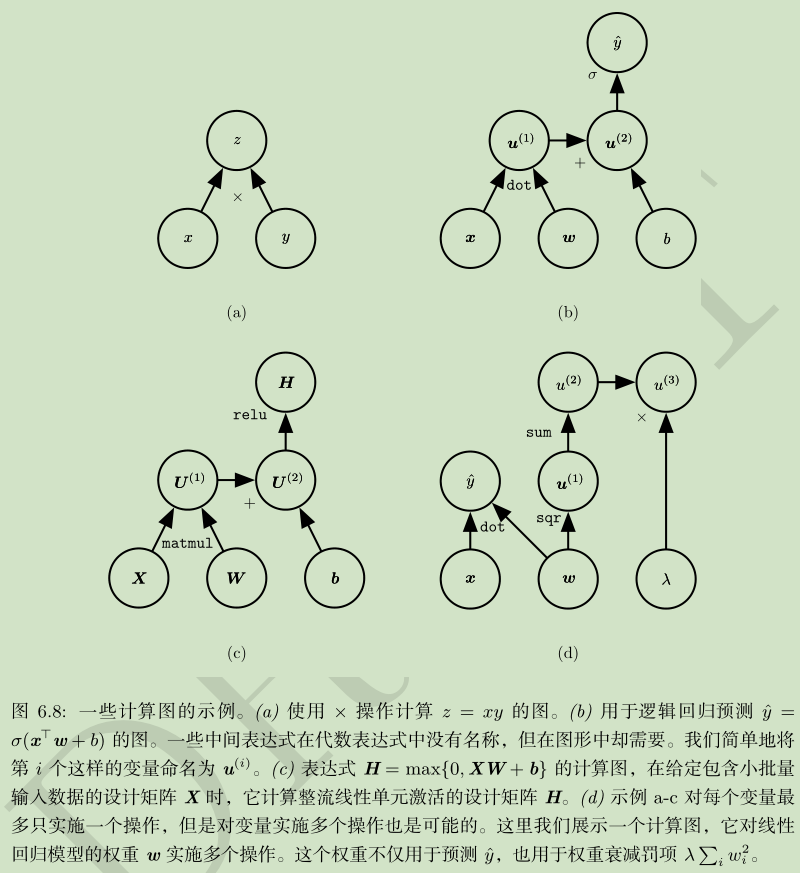
链式求导:
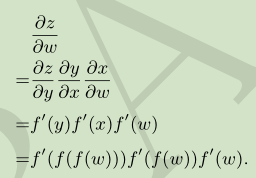
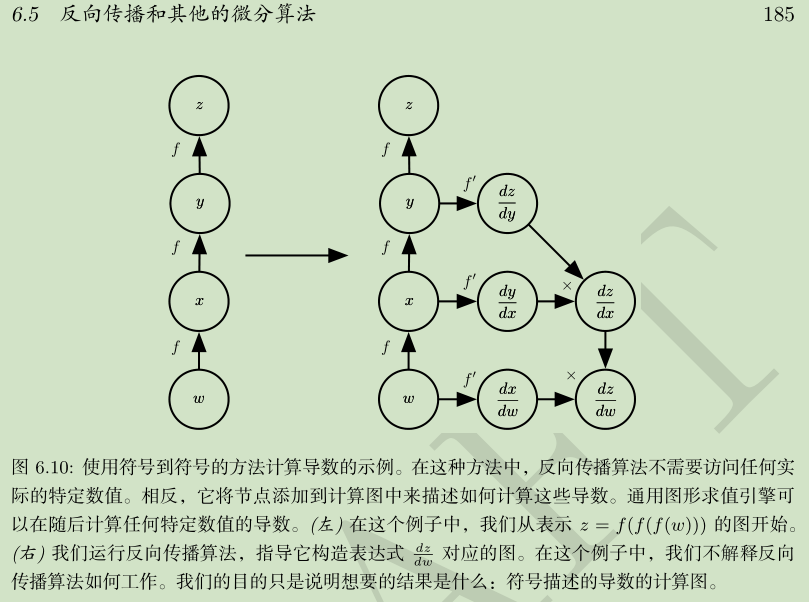
要点:
链式求导:导数=倍率
计算图
符号求导
损失函数
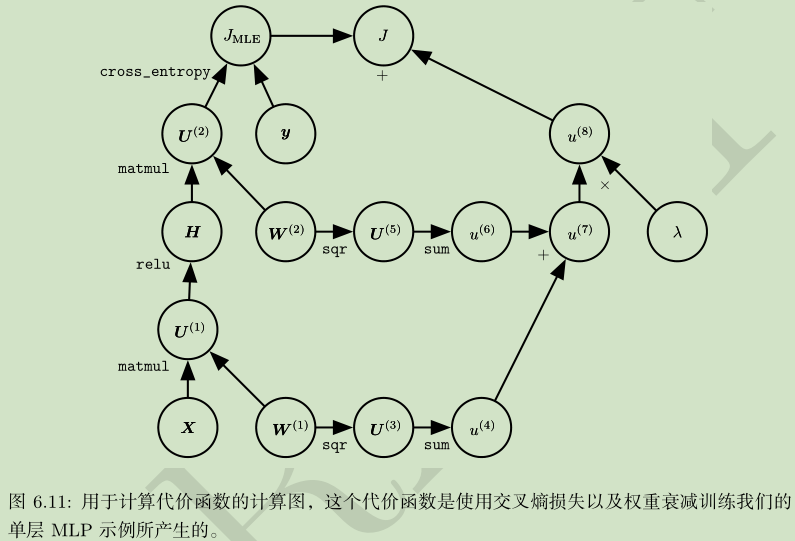
五、隐藏单元
如何选择隐藏单元的类型?
ReLU必定是极好的!
隐藏单元的选择建议
Relu及其扩展:绝对值整流,泄露整流,参数整流
Logistic sigmoid及双曲正切:易饱和,不宜做隐含层单元
径向基(RBF):radical basis function,大部分饱和到零,难以优化
softplus:ReLU的平滑版,实际效果不如ReLU好
硬双曲正切:hard tanh
其他
六、架构设计
有多少个单元,怎么连接?
神经网络大多是链式架构(俄罗斯套娃)
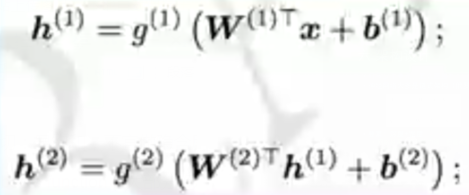

要素:深度+宽度
网络越深,泛化能力越强,但越难优化
深度和宽度折中
理想的架构需要不断实验
能自动学习网络深度吗?——可以,见书中“通用近似定理”?辩证去看
分段线性网络(ReLU或maxout)可表示区域数量跟深度成指数关系
网络越深,泛化越好。
七、总结
自1980年以来,前馈网络核心思想并无多大变化,仍然是梯度下降和反向传播
1986-2015,网络性能出现重大提升,原因是:
大量的数据降低网络泛化难度
硬件和软件能力的提升
部分算法上的进步:交叉熵替换均方差,ReLU的出现
80年代就有ReLU,但是被sigmoid替代,直到2009年才开始变天,原因:
网络非常小,sigmoid表现较好
迷信:必须避免不可导的激活函数
ReLU比隐含层权重还要重要,是系统性能提升的唯一因素
ReLU具备生物神经元的特性:阈值以下不活跃,阈值以上开始活跃,且活跃程度成正比
2006-2012,人们普遍不看好前馈网络,而今前馈网络表现非常好,进一步发展出变分自动编码器和生产对抗网络(GAN)
附:学习金字塔,给有心人
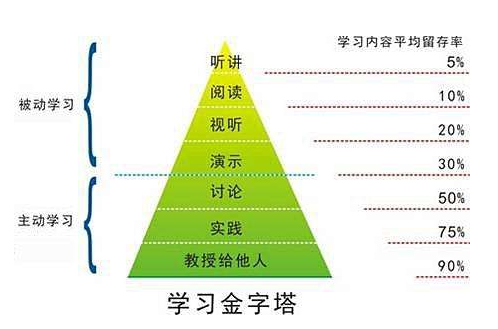
深度学习Bible学习笔记:第六章 深度前馈网络的更多相关文章
- JVM学习笔记-第六章-类文件结构
JVM学习笔记-第六章-类文件结构 6.3 Class类文件的结构 本章中,笔者只是通俗地将任意一个有效的类或接口锁应当满足的格式称为"Class文件格式",实际上它完全不需要以磁 ...
- Android群英传笔记——第六章:Android绘图机制与处理技巧
Android群英传笔记--第六章:Android绘图机制与处理技巧 一直在情调,时间都是可以自己调节的,不然世界上哪有这么多牛X的人 今天就开始读第六章了,算日子也刚好一个月了,一个月就读一半,这效 ...
- 深入理解 C 指针阅读笔记 -- 第六章
Chapter6.h #ifndef __CHAPTER_6_ #define __CHAPTER_6_ /*<深入理解C指针>学习笔记 -- 第六章*/ typedef struct _ ...
- 深度学习Bible学习笔记:第一章 前言
写在前面:请务必踏踏实实看书,结合笔记或视频来理解学习,任何技术,啃砖头是最扎实最系统的,为避免知识碎片化,切忌抛却书本的学习!!! 一 什么是深度学习 1 关于AI: AI系统必须具备从原始数据提取 ...
- C Primer Plus 学习笔记 -- 前六章
记录自己学习C Primer Plus的学习笔记 第一章 C语言高效在于C语言通常是汇编语言才具有的微调控能力设计的一系列内部指令 C不是面向对象编程 编译器把源代码转化成中间代码,链接器把中间代码和 ...
- Linux学习笔记(第六章)
第六章-档案权限与目录配置#chgrp:改变档案的所属群组#chown:改变档案的拥有者#chmod:改变档案的权限及属性 chown用法 chmod用法: r:4 w:2 x:1对于文档: 对于目录 ...
- o'Reill的SVG精髓(第二版)学习笔记——第六章
第六章:坐标系统变换 想要旋转.缩放或者移动图片到新的位置.可以给对应的SVG元素添加transform属性. 6.1 translate变换 可以为<use>元素使用x和y属性,以在特性 ...
- 学习笔记 第六章 使用CSS美化图片
第六章 使用CSS美化图片 6.1 在网页中插入图片 GIF图像 跨平台能力,无兼容性问题: 具有减少颜色显示数目而极度压缩文件的能力,不会降低图像的品质(无损压缩): 支持背景透明功能,便于图像 ...
- 韩松毕业论文笔记-第六章-EFFICIENT METHODS AND HARDWARE FOR DEEP LEARNING
难得跟了一次热点,从看到论文到现在已经过了快三周了,又安排了其他方向,觉得再不写又像之前读过的N多篇一样被遗忘在角落,还是先写吧,虽然有些地方还没琢磨透,但是paper总是这样吧,毕竟没有亲手实现一下 ...
随机推荐
- pandas简短介绍
1.数据结构 维数 名称 描述 1 Series 一维带标签单一数据类型的数组 2 DataFrame 不同数据类型的列 2.十分钟学习pandas 2.1.导入所需模块 import pandas ...
- vue props的理解
vue用了这么久,今天发现父子组件还是傻傻的分不清,不过还好,今天终于搞懂了 vue中到底什么是父组件,什么是子组件 vue之props父子组件之间的谈话 简单的理解就是:使用的地方是父组件,定义的地 ...
- C#复习正则表达式
由于前段时间为了写工具学的太J8粗糙 加上最近一段时间太浮躁 所以静下心来复习 一遍以前学的很弱的一些地方 1 委托 public delegate double weituo(double a, d ...
- CentOS6.8下搭建zookeeper web界面查看工具node-zk-browser
zookeeper的web界面查看工具Node-ZK-Browser的界面是用nodejs写的今天试着搭建了下. 1. 安装nodejs [root@localhost product]# pwd / ...
- SGU 271 Book Pile
There is a pile of N books on the table. Two types of operations are performed over this pile: - a b ...
- Bellman-Ford算法:POJ No.3169 Layout 差分约束
#define _CRT_SECURE_NO_WARNINGS /* 4 2 1 1 3 10 2 4 20 2 3 3 */ #include <iostream> #include & ...
- 010、base镜像 (2018-12-27 周四)
参考https://www.cnblogs.com/CloudMan6/p/6799197.html 什么是base镜像 不依赖其他镜像,从scratch构建.或者是其他可以作为基础镜 ...
- HDFS2.0架构以及HA详解
HDFS2.0概述 一背景,Hadoop1.0中HDFS和MapReduce在高可用,扩展性等方面存在问题 HDFS存在问题,1,NameNode单点故障,难以应用于在线场景.2,NameNod ...
- CentOS6.8安装配置sonarqube6.4
下载最新版本的sonar(现在改名叫sonarqube) https://www.sonarqube.org/downloads/ 我下载的版本是Sonarqube6.4 1 使用前需要 ...
- $Miller Rabin$总结
\(Miller Rabin\)总结: 这是一个很高效的判断质数的方法,可以在用\(O(logn)\) 的复杂度快速判断一个数是否是质数.它运用了费马小定理和二次探测定理这两个筛质数效率极高的方法. ...
