Spark机器学习(10)：ALS交替最小二乘算法

1. Alternating Least Square

ALS(Alternating Least Square)，交替最小二乘法。在机器学习中，特指使用最小二乘法的一种协同推荐算法。如下图所示，u表示用户，v表示商品，用户给商品打分，但是并不是每一个用户都会给每一种商品打分。比如用户u6就没有给商品v3打分，需要我们推断出来，这就是机器学习的任务。

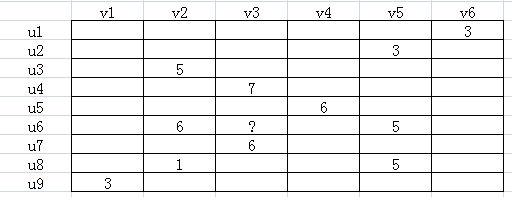
由于并不是每个用户给每种商品都打了分，可以假设ALS矩阵是低秩的，即一个m*n的矩阵，是由m*k和k*n两个矩阵相乘得到的，其中k<<m,n。

A_m×n=U_m×k×V_k×n

这种假设是合理的，因为用户和商品都包含了一些低维度的隐藏特征，比如我们只要知道某个人喜欢碳酸饮料，就可以推断出他喜欢百世可乐、可口可乐、芬达，而不需要明确指出他喜欢这三种饮料。这里的碳酸饮料就相当于一个隐藏特征。上面的公式中，U_m×k表示用户对隐藏特征的偏好，V_k×n表示产品包含隐藏特征的程度。机器学习的任务就是求出U_m×k和V_k×n。可知u_i^Tv_j是用户i对商品j的偏好，使用Frobenius范数来量化重构U和V产生的误差。由于矩阵中很多地方都是空白的，即用户没有对商品打分，对于这种情况我们就不用计算未知元了，只计算观察到的(用户,商品)集合R。

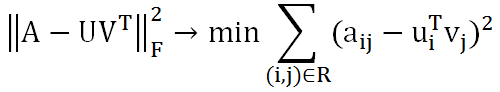
这样就将协同推荐问题转换成了一个优化问题。目标函数中U和V相互耦合，这就需要使用交替二乘算法。即先假设U的初始值_U⁽⁰⁾，这样就将问题转化成了一个最小二乘问题，可以根据_U⁽⁰⁾可以计算出_V⁽⁰⁾，再根据_V⁽⁰⁾计算出_U⁽¹⁾，这样迭代下去，直到迭代了一定的次数，或者收敛为止。虽然不能保证收敛的全局最优解，但是影响不大。

2. MLlib的ALS实现

MLlib的ALS采用了数据分区结构，即将U分解成u₁,u₂,u₃,...u_m，V分解成v₁,v₂,v₃,...v_n，相关的u和v存放在同一个分区，从而减少分区间数据交换的成本。比如通过U计算V时，存储u的分区是P₁,P₂...，存储v的分区是Q₁,Q₂...，需要将不同的u发送给不同的Q，存放这个关系的块称作OutBlock；在P中，计算v时需要哪些u，存放这个关系的块称作InBlock。

比如R中有a₁₂,a₁₃,a₁₅，u₁存放在P₁，v₂,v₃存放在Q₂，v₅存放在Q₃，则需要将P₁中的u₁发送给Q₂和Q₃，这个信息存储在OutBlock；R中有a₁₂,a₃₂，因此计算v₂需要u₁和u₃，这个信息存储在InBlock。

直接上代码：

import org.apache.log4j.{ Level, Logger }
import org.apache.spark.{ SparkConf, SparkContext }
import org.apache.spark.mllib.recommendation.ALS
import org.apache.spark.mllib.recommendation.Rating

/**
  * Created by Administrator on 2017/7/19.
  */
object ALSTest01 {

  def main(args:Array[String]) ={
    // 设置运行环境
    val conf = new SparkConf().setAppName("ALS 01")
      .setMaster("spark://master:7077").setJars(Seq("E:\\Intellij\\Projects\\MachineLearning\\MachineLearning.jar"))
    val sc = new SparkContext(conf)
    Logger.getRootLogger.setLevel(Level.WARN)

    // 读取样本数据并解析
    val dataRDD = sc.textFile("hdfs://master:9000/ml/data/test.data")
    val ratingRDD = dataRDD.map(_.split(',') match {
      case Array(user, item, rate) =>
        Rating(user.toInt, item.toInt, rate.toDouble)
    })

    // 拆分成训练集和测试集
    val dataParts = ratingRDD.randomSplit(Array(0.8, 0.2))
    val trainingRDD = dataParts(0)
    val testRDD = dataParts(1)

    // 建立ALS交替最小二乘算法模型并训练
    val rank = 10
    val numIterations = 10
    val alsModel = ALS.train(trainingRDD, rank, numIterations, 0.01)

    // 预测
    val user_product = trainingRDD.map {
      case Rating(user, product, rate) =>
        (user, product)
    }
    val predictions =
      alsModel.predict(user_product).map {
        case Rating(user, product, rate) =>
          ((user, product), rate)
      }

    val ratesAndPredictions = trainingRDD.map {
      case Rating(user, product, rate) =>
        ((user, product), rate)
    }.join(predictions)

    val MSE = ratesAndPredictions.map {
      case ((user, product), (r1, r2)) =>
        val err = (r1 - r2)
        err * err
    }.mean()

    println("Mean Squared Error = " + MSE)

    println("User" + "\t" + "Products" + "\t" + "Rate" + "\t" + "Prediction")
    ratesAndPredictions.collect.foreach(
      rating => {
        println(rating._1._1 + "\t" + rating._1._2 + "\t" + rating._2._1 + "\t" + rating._2._2)
      }
    )

  }

}

其中ALS.train()函数的4个参数分别是训练用的数据集，特征数量，迭代次数，和正则因子。

运行结果：

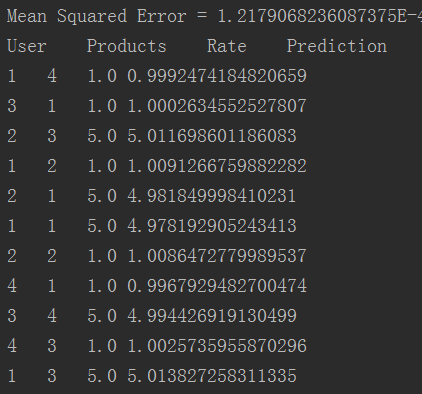
可见，预测结果还是非常准确的。