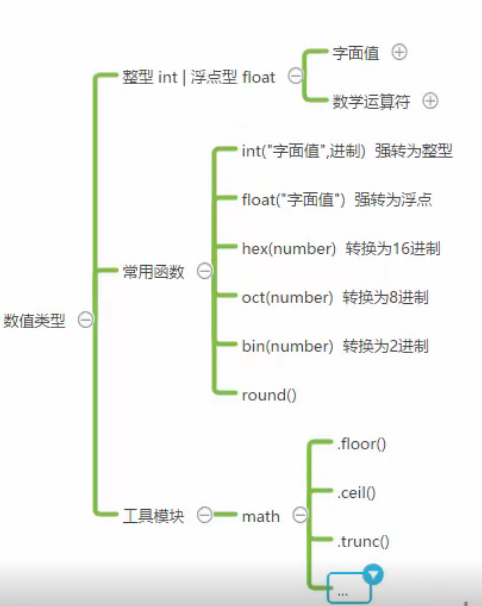
python hex() oct() bin() math 内置函数

示例：

print hex(20),hex(-20) #转换成十六进制
print oct(20),oct(-20) #转换成八进制
print bin(20),bin(-20) #转换成二进制

print int("字面值", 进制)    #转换整型
print float("字面值")      #转换浮点型

print round(浮点型)      #浮点型四舍五入

math方法：
　　math.pi　　　　　= π　　  值3.141592653
　　math.pow(2,4)　　= 16　　2的4次方
　　math.sqrt(144)　　= 12　　144开平方=12