四、Logisitic Regssion练习（转载）

转载：http://www.cnblogs.com/tornadomeet/archive/2013/03/16/2963919.html

牛顿法：http://blog.csdn.net/xp215774576/article/details/45974081

http://blog.csdn.net/luoleicn/article/details/6527049

前言：

　　本节来练习下logistic regression相关内容，参考的资料为网页：http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearning&doc=exercises/ex4/ex4.html。这里给出的训练样本的特征为80个学生的两门功课的分数，样本值为对应的同学是否允许被上大学，如果是允许的话则用’1’表示，否则不允许就用’0’表示，这是一个典型的二分类问题。在此问题中，给出的80个样本中正负样本各占40个。而这节采用的是logistic regression来求解，该求解后的结果其实是一个概率值，当然通过与0.5比较就可以变成一个二分类问题了。

　　实验基础：

　　在logistic regression问题中，logistic函数表达式如下：

　　

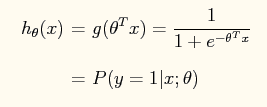
　　这样做的好处是可以把输出结果压缩到0~1之间。而在logistic回归问题中的损失函数与线性回归中的损失函数不同，这里定义的为：

　　

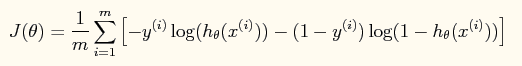
　　如果采用牛顿法来求解回归方程中的参数，则参数的迭代公式为：

　　

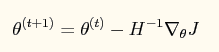
　　其中一阶导函数和hessian矩阵表达式如下：

　　

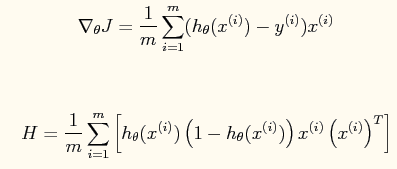
　　当然了，在编程的时候为了避免使用for循环，而应该直接使用这些公式的矢量表达式（具体的见程序内容）。

　　一些matlab函数：

　　find:

　　是找到的一个向量，其结果是find函数括号值为真时的值的下标编号。

　　inline:

　　构造一个内嵌的函数，很类似于我们在草稿纸上写的数学推导公式一样。参数一般用单引号弄起来，里面就是函数的表达式，如果有多个参数，则后面用单引号隔开一一说明。比如：g = inline('sin(alpha*x)','x','alpha')，则该二元函数是g(x,alpha) = sin(alpha*x)。

　　实验结果：

　　训练样本的分布图以及所学习到的分类界面曲线：

　　

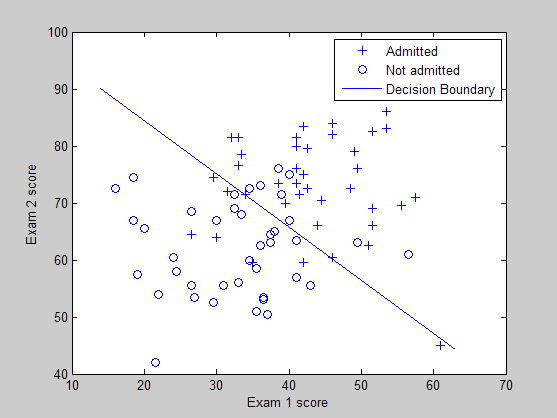
　　损失函数值和迭代次数之间的曲线：

　　

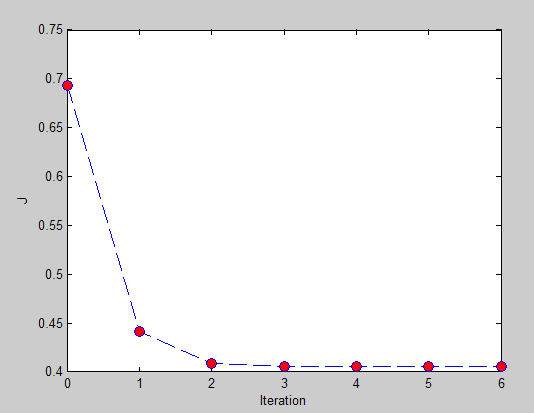
　　最终输出的结果：

　　

　　可以看出当一个小孩的第一门功课为20分，第二门功课为80分时，这个小孩不允许上大学的概率为0.6680，因此如果作为二分类的话，就说明该小孩不会被允许上大学。

　　实验代码（原网页提供）% Exercise -- Logistic Regressio

clear all; close all; clc

x = load('ex4x.dat');
y = load('ex4y.dat');

[m, n] = size(x);

% Add intercept term to x
x = [ones(m, ), x]; 

% Plot the training data
% Use different markers for positives and negatives
figure
pos = find(y); neg = find(y == );%find是找到的一个向量，其结果是find函数括号值为真时的值的编号
plot(x(pos, ), x(pos,), '+')
hold on
plot(x(neg, ), x(neg, ), 'o')
hold on
xlabel('Exam 1 score')
ylabel('Exam 2 score')

% Initialize fitting parameters
theta = zeros(n+, );

% Define the sigmoid function
g = inline('1.0 ./ (1.0 + exp(-z))'); 

% Newton's method
MAX_ITR = ;
J = zeros(MAX_ITR, );

for i = :MAX_ITR
    % Calculate the hypothesis function
    z = x * theta;
    h = g(z);%转换成logistic函数

    % Calculate gradient and hessian.
    % The formulas below are equivalent to the summation formulas
    % given in the lecture videos.
    grad = (/m).*x' * (h-y);%梯度的矢量表示法
    H = (/m).*x' * diag(h) * diag(1-h) * x;%hessian矩阵的矢量表示法

    % Calculate J (for testing convergence)
    J(i) =(/m)*sum(-y.*log(h) - (-y).*log(-h));%损失函数的矢量表示法

    theta = theta - H\grad;%此处的\右除表示H的逆矩阵乘grad
end
% Display theta
theta

% Calculate the probability that a student with
% Score  on exam  and score  on exam
% will not be admitted
prob =  - g([, , ]*theta)

%画出分界面
% Plot Newton's method result
% Only need  points to define a line, so choose two endpoints
plot_x = [min(x(:,))-,  max(x(:,))+];
% Calculate the decision boundary line，plot_y的计算公式见博客下面的评论。
plot_y = (-./theta()).*(theta().*plot_x +theta()); 直接令logistic回归的值为0.5，则可以得到e的指数为0，即：

%theta(1)*1+theta(2)*plot_x+theta(3)*plot_y=0,解出plot_y即可。
plot(plot_x, plot_y)
legend('Admitted', 'Not admitted', 'Decision Boundary')
hold off

% Plot J
figure
plot(:MAX_ITR-, J, 'o--', 'MarkerFaceColor', 'r', 'MarkerSize', )
xlabel('Iteration'); ylabel('J')
% Display J

参考资料：

http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearning&doc=exercises/ex4/ex4.html