P3911 最小公倍数之和

终于找到了一个只会用[gcd(i,j)==1] = sigema d|gcd(i,j) mu(d) 做不了的题。

考虑枚举gcd后。

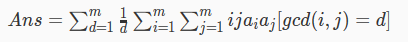
此时，ans可以表示为一个 sigema x f(x)的形式。

考虑对反演f(x)。

然后发现f(x)也很容易在nlogn的复杂度内算出来，就做完了。

#include<bits/stdc++.h>
#define N 110000
#define eps 1e-7
#define inf 1e9+7
#define db double
#define ll long long
#define ldb long double
using namespace std;
inline ll read()
{
	char ch=0;
	ll x=0,flag=1;
	while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
	while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
	return x*flag;
}
bool is_prime[N];
ll a[N],f[N],mu[N],prime[N];
void solve(ll n)
{
	memset(is_prime,true,sizeof(is_prime));
	is_prime[0]=is_prime[1]=false;mu[0]=mu[1]=1;
	for(ll i=2,cnt=0;i<=n;i++)
	{
		if(is_prime[i])prime[++cnt]=i,mu[i]=-1;
		for(ll j=1;j<=cnt;j++)
		{
			if(i*prime[j]>n)break;
			is_prime[i*prime[j]]=false;
			if(i%prime[j])mu[i*prime[j]]=-mu[i];
			else{mu[i*prime[j]]=0;break;}
		}
	}
}
int main()
{
	ll n=read(),len=5e4;solve(len);
	for(ll i=1;i<=n;i++)a[read()]++;
	for(ll i=1;i<=len;i++)
	{
		for(ll j=i;j<=len;j+=i)f[i]+=a[j]*j;
		f[i]*=f[i];
	}
	ll ans=0;
	for(ll i=1;i<=len;i++)
	{
		ll tot=0;
		for(ll j=i;j<=len;j+=i)tot+=mu[j/i]*f[j];
		ans+=tot/i;
	}
	printf("%lld",ans);
	return 0;
}